Dijkstra单源点最短路径算法

学习参考：

Dijkstra算法（单源最短路径）

最短路径—Dijkstra算法和Floyd算法

使用的图结构：

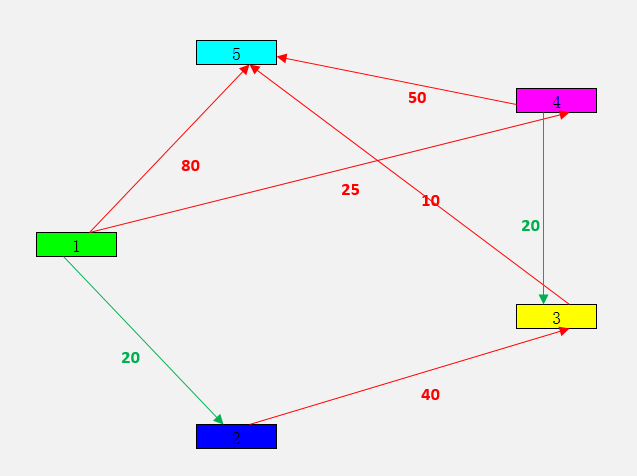
邻接矩阵：

-1 20 -1 25 80
-1 -1 40 -1 -1
-1 -1 -1 -1 10
-1 -1 20 -1 50
-1 -1 -1 -1 -1

代码：

     void Dijkstra(){//单源点最短路径
         int i,j;
         boolean s[]=new boolean[vexnum];
         int dist[]=new int[vexnum];
         int prev[]=new int[vexnum];
         int v=0;
         for(i=0;i<vexnum;i++){
             dist[i]=adjMatrix[v][i];
             s[i]=false;
             if(dist[i]>0){
                 prev[i]=v;
             }else{
                 prev[i]=-1;
             }
         }
         dist[v]=0;
         s[v]=true;
         for(i=1;i<vexnum;i++){
             int u=v;
             int min=0x7FFFFFFF;
             for(j=0;j<vexnum;j++){//把dist中的最小值加入S
                 if(s[j]==false && (dist[j]<min) && dist[j]!=-1){//j不在s中 ，j比最小值小
                     u=j;
                     min=dist[j];
                 }
             }
             s[u]=true;//结点u加入S中
             //利用结点u更新dist
             for(j=0;j<vexnum;j++){
                 if(s[j]==false && adjMatrix[u][j]!=-1){//j不在s中，并且u->j连通
                     int newdist=dist[u]+adjMatrix[u][j];//v->u + u->j
                     if(newdist<dist[j] || dist[j]==-1){
                         dist[j]=newdist;
                         prev[j]=u;
                     }
                 }
             }
         }
         //-1 0 3 0 2
         for(i=1;i<vexnum;i++){
             System.out.print(i);
             int t=prev[i];
             while(t!=-1){
                 System.out.print("<--"+t);
                 t=prev[t];
             }
             System.out.println();
         }
     }

输出：

1<--0
2<--3<--0
3<--0
4<--2<--3<--0

另外一个测试数据：

可视化图结构：

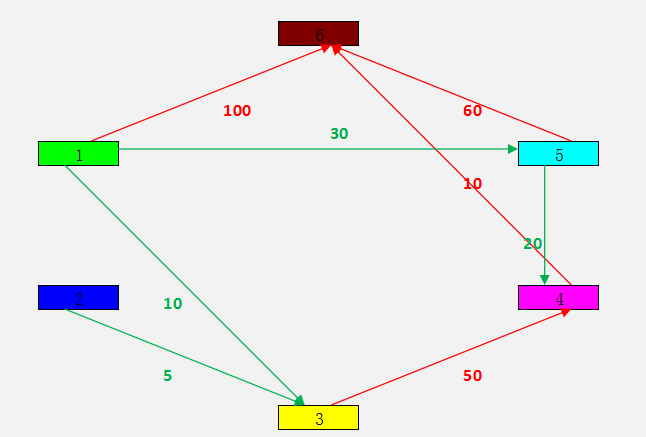
邻接矩阵：

-1 -1 10 -1 30 100
-1 -1 5 -1 -1 -1
-1 -1 -1 50 -1 -1
-1 -1 -1 -1 -1 10
-1 -1 -1 20 -1 60
-1 -1 -1 -1 -1 -1

输出：

1
2<--0
3<--4<--0
4<--0
5<--3<--4<--0