luoguP3003 [USACO10DEC]苹果交货Apple Delivery

LOL新英雄卡莎点击就送

一句话题意：

三个点a1,a2,b，求从b到a1和a2的最短路

做法：求出a1->b和a2->b的最短路，两者取min，之后再加上a1->a2的最短路

为啥呢

由于题目中说：没有路会从另一个牧场走回自己

所以图只有以下三种情况

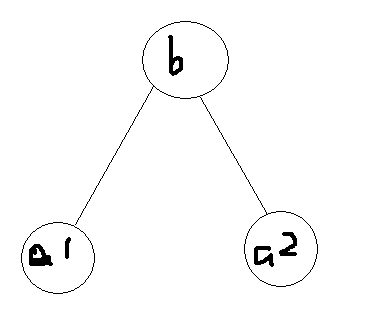
emmmmmmm

懂了吗

另外注意裸的SPFA会TLE3个点，可以用SLF优化(有人说LLL会TLE4个……)

堆优化Dijkstra可以直接过

下面给出SPFA的代码和堆优化Dijkstra的代码

#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
const int N=,M=;
#define gc() (SS==TT &&(TT=(SS=IN)+fread(IN,1,1<<20,stdin),SS==TT)?EOF:*SS++)
char IN[<<],*SS=IN,*TT=IN;
int n,m,st,e1,e2,q[N+M],h[N];
struct Edge{
    int u,v,w,nxt;
}edge[M<<];
bool vis[N];
int dis[N],num;
inline int read()
{
    int n=,w=;register char c=gc();
    while(c>''||c<''){if(c=='-')w=-;c=gc();}
    while(c>=''&&c<='')n=n*+c-'',c=gc();
    return n*w;
}
inline void add(int u,int v,int w)
{
    edge[++num].u=u;
    edge[num].v=v;
    edge[num].w=w;
    edge[num].nxt=h[u];
    h[u]=num;
}
inline void SPFA(int s)
{
    memset(dis,0x7f,sizeof dis);
    int head=,tail=;
    q[++tail]=s;
    dis[s]=;vis[s]=true;
    while(head<tail)
    {
        int now=q[++head];
        vis[now]=false;
        for(int v,i=h[now];i;i=edge[i].nxt)
        {
            v=edge[i].v;
            if(dis[v]>dis[edge[i].u]+edge[i].w)
            {
                dis[v]=dis[edge[i].u]+edge[i].w;
                if(!vis[v])
                {
                    vis[v]=true;
                    if(dis[v]>dis[q[head+]]||head==tail)
                        q[++tail]=v;
                    else    q[head--]=v;//双端队列
                }
            }
        }
    }
}
int main()
{
    m=read(),n=read(),st=read(),e1=read(),e2=read();
    for(int u,v,w,i=;i<m;++i)
    {
        u=read(),v=read(),w=read();
        add(u,v,w);add(v,u,w);
    }
    int ans1,ans2;
    SPFA(e1);
    ans1=dis[st]+dis[e2];
    SPFA(e2);
    ans2=dis[st]+dis[e1];
    printf("%d",std::min(ans1,ans2));
    return ;
}

SLF优化SPFA

// luogu-judger-enable-o2
#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int N=,M=;
#define gc() (SS==TT &&(TT=(SS=IN)+fread(IN,1,1<<20,stdin),SS==TT)?EOF:*SS++)
#define pr pair<int,int>
#define mp make_pair
int n,m,st,e1,e2,head[N];
struct Edge{
    int v,w,nxt;
}edge[M<<];
bool vis[N];
int dis[N],num;
char IN[<<],*SS=IN,*TT=IN;
std::priority_queue<pr,vector<pr>,greater<pr> > que;
inline int read()
{
    int n=,w=;register char c=gc();
    while(c>''||c<''){if(c=='-')w=-;c=gc();}
    while(c>=''&&c<='')n=n*+c-'',c=gc();
    return n*w;
}
inline void add(int u,int v,int w)
{
    edge[++num].v=v;
    edge[num].w=w;
    edge[num].nxt=head[u];
    head[u]=num;
}
inline void Dijkstra(int s)
{
    memset(dis,0x6f,sizeof dis);
    memset(vis,false,sizeof vis);
    dis[s]=;que.push(mp(,s));
    int emp;
    while(!que.empty())
    {
        emp=que.top().second;que.pop();
        if(vis[emp])continue;
        vis[emp]=true;
        for(int i=head[emp];i;i=edge[i].nxt)
            if(dis[edge[i].v]>dis[emp]+edge[i].w)
            {
                dis[edge[i].v]=dis[emp]+edge[i].w;
                que.push(mp(dis[edge[i].v],edge[i].v));
            }
    }
}

int main()
{
    m=read(),n=read(),st=read(),e1=read(),e2=read();
    for(int u,v,w,i=;i<m;++i)
    {
        u=read(),v=read(),w=read();
        add(u,v,w);add(v,u,w);
    }
    int ans1,ans2;
    Dijkstra(e1);
    ans1=dis[e2]+dis[st];
    Dijkstra(e2);
    ans2=dis[e1]+dis[st];
    printf("%d",std::min(ans1,ans2));
    return ;
}

堆优化Dijkstra

#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int N=,M=;
#define pr pair<int,int>
#define mp make_pair
int n,m,st,e1,e2,head[N];
struct Edge{
    int u,v,w,nxt;
}edge[M<<];
bool vis[N];
int dis[N],num;
std::priority_queue<pr,vector<pr>,greater<pr> > que;
inline int read()
{
    int n=,w=;register char c=getchar();
    while(c>''||c<''){if(c=='-')w=-;c=getchar();}
    while(c>=''&&c<='')n=n*+c-'',c=getchar();
    return n*w;
}
inline void add(int u,int v,int w)
{
    edge[num].u=u;
    edge[num].v=v;
    edge[num].w=w;
    edge[num].nxt=head[u];
    head[u]=num++;
    return ;
}
inline int Dijkstra(int s,int e)
{
    memset(dis,0x6f,sizeof dis);
    memset(vis,false,sizeof vis);
    while(!que.empty())que.pop();
    dis[s]=;que.push(mp(,s));
    int emp;
    while(!que.empty())
    {
        emp=que.top().second;que.pop();
        if(vis[emp])continue;
        vis[emp]=true;
        if(emp==e)return dis[e];
        for(int i=head[emp];i!=-;i=edge[i].nxt)
            if(dis[edge[i].v]>dis[emp]+edge[i].w)
            {
                dis[edge[i].v]=dis[emp]+edge[i].w;
                que.push(mp(dis[edge[i].v],edge[i].v));
            }
    }
    return dis[e];
}

int main()
{
    memset(head,-,sizeof head);
    m=read(),n=read(),st=read(),e1=read(),e2=read();
    for(int u,v,w,i=;i<m;++i)
    {
        u=read(),v=read(),w=read();
        add(u,v,w);add(v,u,w);
    }
    int ans1,ans2;
    ans1=Dijkstra(st,e1);
    ans2=Dijkstra(st,e2);
    printf("%d",std::min(ans1,ans2)+Dijkstra(e1,e2));
    return ;
}

真·堆优化Dijkstra

后两个的区别主要是跑两遍与跑三遍……