推荐算法之Thompson(汤普森)采样

如果想理解汤普森采样算法，就必须先熟悉了解贝塔分布。

一、Beta(贝塔)分布

Beta分布是一个定义在[0,1]区间上的连续概率分布族，它有两个正值参数，称为形状参数，一般用α和β表示，Beta分布的概率密度函数形式如下：

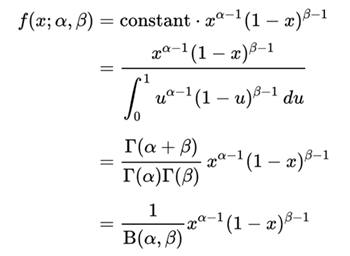
这里的Γ表示gamma函数。

Beta分布的均值是：

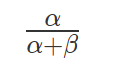
方差：

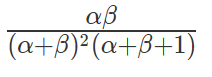
Beta分布的图形(概率密度函数)：

从Beta分布的概率密度函数的图形我们可以看出，Beta分布有很多种形状，但都是在0-1区间内，因此Beta分布可以描述各种0-1区间内的形状（事件）。因此，它特别适合为某件事发生或者成功的概率建模。同时，当α=1，β=1的时候，它就是一个均匀分布。

贝塔分布主要有 α和 β两个参数，这两个参数决定了分布的形状，从上图及其均值和方差的公式可以看出：

1）α/(α+β)也就是均值，其越大，概率密度分布的中心位置越靠近1，依据此概率分布产生的随机数也多说都靠近1，反之则都靠近0。

2）α+β越大，则分布越窄，也就是集中度越高，这样产生的随机数更接近中心位置，从方差公式上也能看出来。

二、举例理解Beta分布

贝塔分布可以看作是一个概率的分布，当我们不知道一个东西的具体概率是多少时，它给出了所有概率出现的可能性大小，可以理解为概率的概率分布。

以棒球为例子：

　　棒球运动的一个指标就是棒球击球率，就是用一个运动员击中的球数除以总的击球数，一般认为0.27是一个平均的击球水平，如果击球率达到0.3就会认为非常优秀了。如果我们要预测一个棒球运动员，他整个赛季的棒球击球率，怎么做呢？你可以直接计算他目前的棒球击球率，用击中数除以击球数。但是，这在赛季开始阶段时是很不合理的。假如这个运动员就打了一次，还中了，那么他的击球率就是100%；如果没中，那么就是0%，甚至打5、6次的时候，也可能运气爆棚全中击球率100%，或者运气很糟击球率0%，所以这样计算出来的击球率是不合理也是不准确的。

为什么呢？

当运动员首次击球没中时，没人认为他整个赛季都会一次不中，所以击球率不可能为0。因为我们有先验期望，根据历史信息，我们知道击球率一般会在0.215到0.36之间。如果一个运动员一开始打了几次没中，那么我们知道他可能最终成绩会比平均稍微差一点，但是一般不可能会偏离上述区间，更不可能为0。

　 如何解决呢？

一个最好的方法来表示这些先验期望（统计中称为先验（prior））就是贝塔分布，表示在运动员打球之前，我们就对他的击球率有了一个大概范围的预测。假设我们预计运动员整个赛季的击球率平均值大概是0.27左右，范围大概是在0.21到0.35之间。那么用贝塔分布来表示，我们可以取参数 α=81，β=219，因为α/(α+β)=0.27，图形分布也主要集中在0.21~0.35之间，非常符合经验值，也就是我们在不知道这个运动员真正击球水平的情况下，我们先给一个平均的击球率的分布。

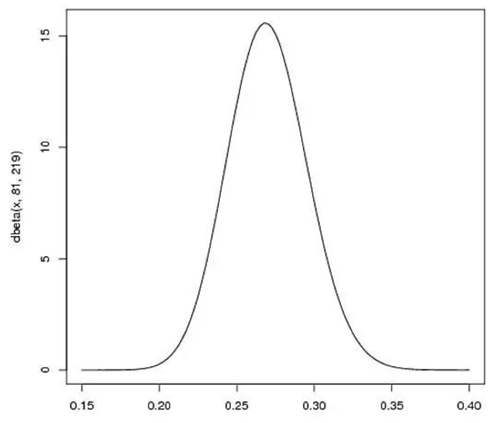
假设运动员一次击中，那么现在他本赛季的记录是“1次打中；1次打击”。那么我们更新我们的概率分布，让概率曲线做一些移动来反应我们的新信息。

　　　　     Beta(α₀+hits，β₀+misses)

注：α₀，β₀是初始化参数，也就是本例中的81，219。hits表示击中的次数，misses表示未击中的次数。

击中一次，则新的贝塔分布为Beta(81+1,219)，一次并不能反映太大问题，所以在图形上变化也不大，不画示意图了。然而，随着整个赛季运动员逐渐进行比赛，这个曲线也会逐渐移动以匹配最新的数据。由于我们拥有了更多的数据，因此曲线（击球率范围）会逐渐变窄。假设赛季过半时，运动员一共打了300次，其中击中100次。那么新的贝塔分布是Beta(81+100,219+200)，如下图：

可以看出，曲线更窄而且往右移动了（击球率更高），由此我们对于运动员的击球率有了更好的了解。新的贝塔分布的期望值为0.303，比直接计算100/(100+200)=0.333要低，是比赛季开始时的预计0.27要高，所以贝塔分布能够抛出掉一些偶然因素，比直接计算击球率更能客观反映球员的击球水平。

总结：

这个公式就相当于给运动员的击中次数添加了“初始值”，相当于在赛季开始前，运动员已经有81次击中219次不中的记录。 因此，在我们事先不知道概率是什么但又有一些合理的猜测时，贝塔分布能够很好地表示为一个概率的分布。

 三、汤普森采样

汤普森采样的背后原理正是上述所讲的Beta分布，你把贝塔分布的 a 参数看成是推荐后用户点击的次数，把分布的 b 参数看成是推荐后用户未点击的次数，则汤普森采样过程如下：

　　1、取出每一个候选对应的参数 a 和 b；
　　2、为每个候选用 a 和 b 作为参数，用贝塔分布产生一个随机数；
　　3、按照随机数排序，输出最大值对应的候选；
　　4、观察用户反馈，如果用户点击则将对应候选的 a 加 1，否则 b 加 1；

注：实际上在推荐系统中，要为每一个用户都保存一套参数，比如候选有 m 个，用户有 n 个，那么就要保存 2 m n个参数。

汤普森采样为什么有效呢？

1）如果一个候选被选中的次数很多，也就是 a+b 很大了，它的分布会很窄，换句话说这个候选的收益已经非常确定了，就是说不管分布中心接近0还是1都几乎比较确定了。用它产生随机数，基本上就在中心位置附近，接近平均收益。

2）如果一个候选不但 a+b 很大，即分布很窄，而且 a/(a+b) 也很大，接近 1，那就确定这是个好的候选项，平均收益很好，每次选择很占优势，就进入利用阶段。反之则有可能平均分布比较接近与0，几乎再无出头之日。

3）如果一个候选的 a+b 很小，分布很宽，也就是没有被选择太多次，说明这个候选是好是坏还不太确定，那么分布就是跳跃的，这次可能好，下次就可能坏，也就是还有机会存在，没有完全抛弃。那么用它产生随机数就有可能得到一个较大的随机数，在排序时被优先输出，这就起到了前面说的探索作用。

python代码实现：

choice = numpy.argmax(pymc.rbeta(1 + self.wins, 1 + self.trials - self.wins))