CSP-S 2019提高组训练 服务器需求

时间限制：C/C++ 3秒

空间限制：C/C++ 262144K

题目描述

小多计划在接下来的n天里租用一些服务器，所有的服务器都是相同的。接下来n天中，第i天需要\(a_i\)台服务器工作，每台服务器只能在这n天中工作m天，这m天可以不连续。

但是计划不是一成不变的，接下来有q次修改计划（修改是永久的），每次修改某一天k的需求量\(a_k\)。

小多希望知道每次修改之后，最少需要多少台服务器。

点击下载大样例

输入描述:

第一行三个正整数n,m,q，分别表示计划的天数，每台服务器能工作的天数和修改次数。

随后一行n个非负整数，第i个数字\(a_i\)​表示原计划第i天需要多少台服务器工作。

随后q行，每行两个正整数\(p_i,c_i\)，表示把第\(p_i\)天需要的服务器数目改成\(c_i\)。

输出描述:

第一行输出原计划需要的最少服务器数量。

随后q行，每行输出对应的修改之后，需要的最少的服务器的数量。

输入

5 3 2

1 1 1 1 1

1 2

2 3

输出

2

2

3

样例说明

未修改时，可以租用2台服务器，分别安排给{1,4,5}和{2,3}这些天。

当第一次修改时，第一天需要两台服务器，需求变为了2 1 1 1 1，故可以安排成{1,2,3}和{1,4,5}，满足所有的需求。

第二次修改时，第二天需要三台服务器，需求变为了2 3 1 1 1。可以安排三台服务器，每台服务器安排的日子分别为{1,2,3},{1,2,4}和{2,5}，这样可以满足所有天的需求。

数据范围

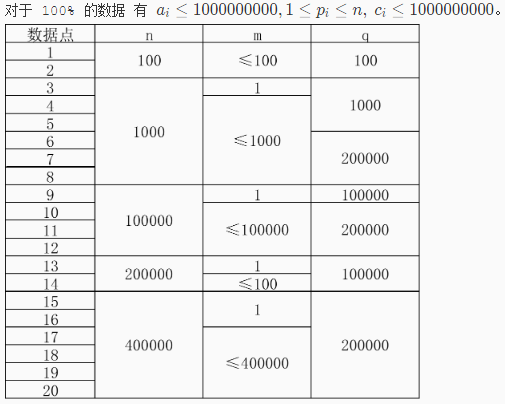
解题思路

\(\color{red}{解法一}\) （m=1） 25分

注意到 m=1 时，\(\sum_{} ai\) 即为答案。

每次修改之后的询问，维护差值即可。

\(\color{red}{解法二}\) （n,q≤100） 10分

考虑如何利用贪心策略。

注意到如果在一开始准备了很多服务器，我们总会优先选择当前服务器使用的剩余天数最多的。

因为 ai 的值可能很大，我们可以考虑维护一个数组 bj，表示当前还可以使用j天的服务器有多少台，每次从最多的开始取。

最初服务器的数量可以二分。时间复杂度 \(\mathcal{O}(nmq \log a_i)\)。

\(\color{red}{解法三}\) （n,q≤1000） 30分

考虑如何利用贪心策略。

注意到其实对于每一种服务器需求，可以直接计算出服务器需要的最少数目即为 \(\max\left(a_i,\lceil\dfrac{\sum a_i}{m}\rceil\right)\)



考虑暴力修改改变位置及之后的前缀和数组，O(n) 计算，时间复杂度 \(\mathcal{O}(nq)\)。

参考实现代码

#include<bits/stdc++.h>
using namespace std;
const int N=4e5+5;
int n,m,q;
long long a[N],tot[N],P[N];
int main()
{
	cin>>n>>m>>q;
	long long tot=0;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		P[i]=P[i-1]+a[i];
	}
	if(m==1|| n>=100000 )    // m==1 时直接算，或者骗分
	{
		long long tmp=P[n];
		cout<<(tmp+m-1)/m<<endl;  //这个地方注意不能直接输出tmp，还要考虑m!=1时的骗分
		int p,c;
		for(int i=1;i<=q;i++)
		{
			cin>>p>>c;
			tmp=tmp+c-a[p];
			a[p]=c;
			cout<<(tmp+m-1)/m<<endl;  //这个地方注意不能直接输出tmp，还要考虑m!=1时的骗分
		}
	}
	else       // m!=1 时， q*n的做法，暴力修改变更后的前缀和
	{
		long long tmp=0,t;
		for(int i=1;i<=n;i++)
		{
			t=max(a[i],(P[i]+m-1)/m);
			tmp=max(tmp,t);
		}
		cout<<tmp<<endl;
		int p,c;
		for(int i=1;i<=q;i++)
		{
			cin>>p>>c;
			int temp=c-a[p];
			for(int k=p;k<=n;k++)  //暴力O(n)更新前缀和
				P[k]=P[k]+temp;
			a[p]=c;
			tmp=0;
			for(int i=1;i<=n;i++)
			{
				t=max(a[i],(P[i]+m-1)/m);
				tmp=max(tmp,t);
			}
			cout<<tmp<<endl;
		}
	}
	return 0;
}

\(\color{red}{解法四}\) （n,q≤1000） 30分

同样是想到了 \(\color{red}{解法三}\) 的贪心策略。

但是在考虑更改操作之后，序列前缀和的修改和前缀和的查询强行套上了一个树状数组，导致复杂度增加一个log，这是最开始想到的一个将问题考虑复杂化的愚蠢做法。时间复杂度 \(\mathcal{O}(nq \log n)\)。

实现代码

#include<bits/stdc++.h>
using namespace std;
const int N=4e5+5;
int n,m,q;
long long a[N],tot[N],P[N];
int lowbit(int x)
{
	return x&(-x);
}
void add(int i,int x)
{
	while(i<=n)
	{
		tot[i]=tot[i]+x;
		i=i+lowbit(i);
	}
}
long long getsum(int k)
{
	long long ans=0;
	while(k>0)
	{
		ans=ans+tot[k];
		k=k-lowbit(k);
	}
	return ans;
}
int main()
{
	cin>>n>>m>>q;
	long long tot=0;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		P[i]=P[i-1]+a[i];
		add(i,a[i]);
	}
	if(m==1|| n>=100000 )    // m==1 时直接算，或者骗分
	{
		long long tmp=P[n];
		cout<<(tmp+m-1)/m<<endl;
		int p,c;
		for(int i=1;i<=q;i++)
		{
			cin>>p>>c;
			tmp=tmp+c-a[p];
			a[p]=c;
			cout<<(tmp+m-1)/m<<endl;  //这个地方注意不能直接输出tmp，还要考虑m!=1时的骗分
		}
	}
	else       // m!=1 时， q*n*log(n) 的做法
	{
		long long tmp=0,t;
		for(int i=1;i<=n;i++)
		{
			t=max(a[i],(P[i]+m-1)/m);
			tmp=max(tmp,t);
		}
		cout<<tmp<<endl;
		int p,c;
		for(int i=1;i<=q;i++)
		{
			cin>>p>>c;
			add(p,c-a[p]);
			a[p]=c;
			long long tmp1=0,t1;
			for(int i=1;i<=n;i++)
			{
				long long sum=getsum(i);
				t1=max(a[i],(sum+m-1)/m);
				tmp1=max(tmp1,t1);
			}
			cout<<tmp1<<endl;
		}
	}
	return 0;
}

\(\color{red}{解法五}\) （n≤400000,q≤200000） 100分

想到了 \(\color{red}{解法三}\) 的贪心策略，其实距离正解已经非常的接近了。在解法三的基础上需要进行优化的是O(n)暴力的去更新每一个修改操作之后的前缀和。

这个问题的瓶颈就在此，每次的修改操作是否需要将后面每一项前缀和都进行更新？

回到那个具有迷惑性的式子，考虑每个任务序列的最少服务器需求为：\(\color{red}{max}\) { $ \max\left(a_i,\lceil\dfrac{\sum_1^i a_i}{m}\rceil\right) $} (i=1~n)

结合方法三的证明过程，经过分析发现，实际上这个式子的答案为： \(\max\left\{\lceil\frac{\sum_{i=1}^na_i}{m}\rceil,\max_{1\le i \le n}a_i\right\}\) .

因此每次的修改操作只需要维护整个任务序列中的最大值，同时更新整个序列的和即可。

需要一个简单的数据结构来支持删除和增加一个值并维护最大值。利用 Priority_queue 或者 multiset 或其他简单数据结构可以维护这个操作。

时间复杂度 \(\mathcal{O}(n\log n+q\log n)\)。

参考实现代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define maxn 200005
ll n,m,t,a[2*maxn],maxx,sum=0;
priority_queue<pair<ll,ll> >q;
int main()
{
	cin>>n>>m>>t;
	for(ll i=1;i<=n;i++)
	{
	    cin>>a[i];
	    q.push(make_pair(a[i],i));
	    sum+=a[i];
	}
	cout<<max(q.top().first,(sum+m-1)/m)<<endl; //注意答案要向上取整
	for(ll i=1;i<=t;i++)
	{
	    ll p,c;
	    cin>>p>>c;
	    sum+=c-a[p];
	    a[p]=c;
	    q.push(make_pair(a[p],p));
	    // 对于每次取出大根堆中最大元素值，要是当前最新序列的最大元素ai.
	    while(q.top().first!=a[q.top().second]) q.pop(); //否则要删除修改之后堆中的历史节点
	    cout<<max(q.top().first,(sum+m-1)/m)<<endl;
	}
	return 0;
}

#include<bits/stdc++.h>
using namespace std;
long long a[400010],n;
multiset<long long>q;
int main()
{
    long long m,k,s=0;
    cin>>n>>m>>k;
    for(long long i=1;i<=n;i++)
	{
        cin>>a[i];
        s+=a[i];
        q.insert(a[i]);
    }
    cout<<max((s+m-1)/m,*q.rbegin())<<endl;
    for(long long i=1;i<=k;i++)
	{
        long long x,y;
        cin>>x>>y;
        s+=(y-a[x]);
        q.erase(q.find(a[x]));
        q.insert(a[x]=y);
        cout<<max((s+m-1)/m,*q.rbegin())<<endl;
    }
    return 0;
}