神经网络(12)--具体实现:如何对back propagation的正确性进行验证

我们在进行back propagation时难免会出现各种各样的问题，当出现问题的时候，我们的cost function仍然是随着迭代的次数下降的，但是这中间会有一些问题存在，那么我们如何来检查我们的算法是否会出现这些不易被发现的问题呢？

gradients的近似表达

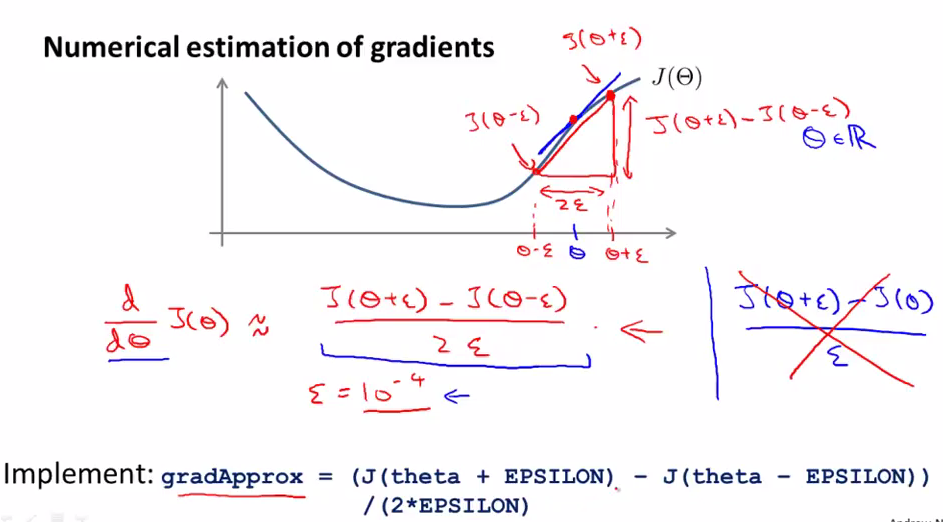
上面是导数的近似表达式，取左边的双边近似而不是右边的单边近似，通常ξ取10^-4,如果取得太小则会给计算带来很大的麻烦。

θ是unrolled vector时，计算J(θ)对θ_i的导数的近似值

用for来实现求导的近似表达

theta为神经网络中所有的参数组成的向量，我们对所有的参数分别求导来计算gradApprox.

我们通过back propagation计算的DVec是对所有参数的导数，我们通过比较gradApprox与DVec这两个数是否是近似相等来判断我们的back propagation是否是正确的。

实现时需要注意的一些问题

在我们检查完back propagation是正确的后，进行学习前，我们要将gradient checking关掉。因为我们使用back propagation对导数进行计算比用numerical gradient algorithmn来计算要快得多，所以在我们验证back propagation是正确的后，在training your classifier之前，我们要将gradient checking code关掉。

总结

在我们实现back propagation或者一种复杂的算法的时候，我们通常会使用numerical gradient来验证其是否正确。