基于STM32Cube的DAC数模转化
1. STM32Cube配置
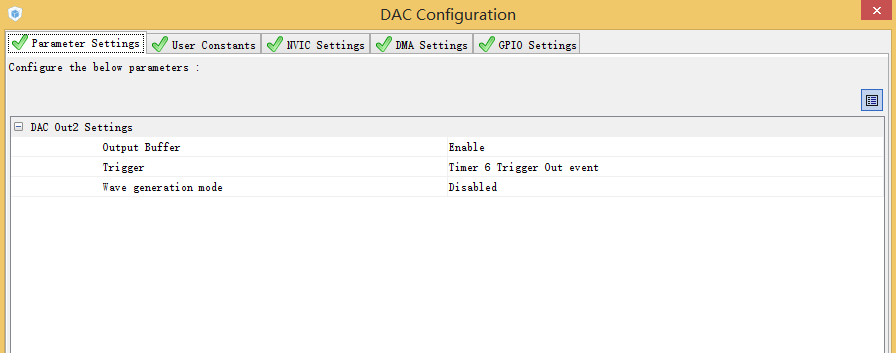
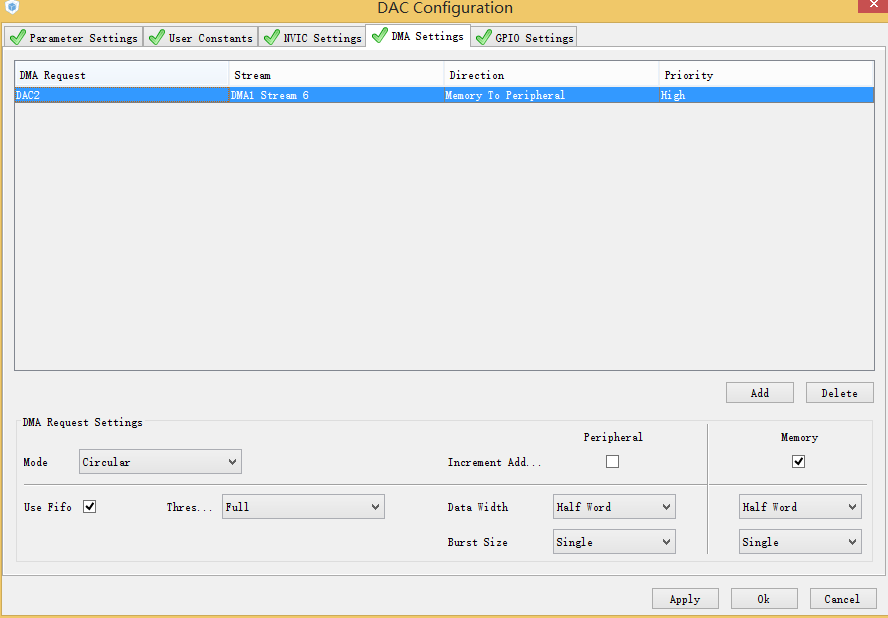
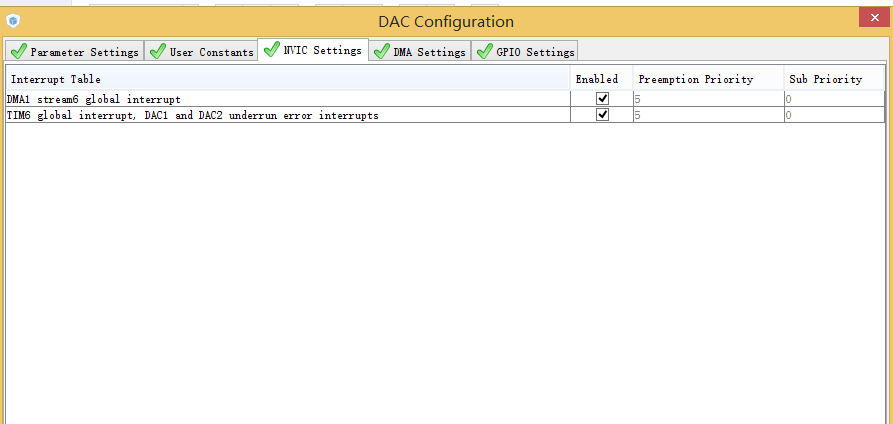
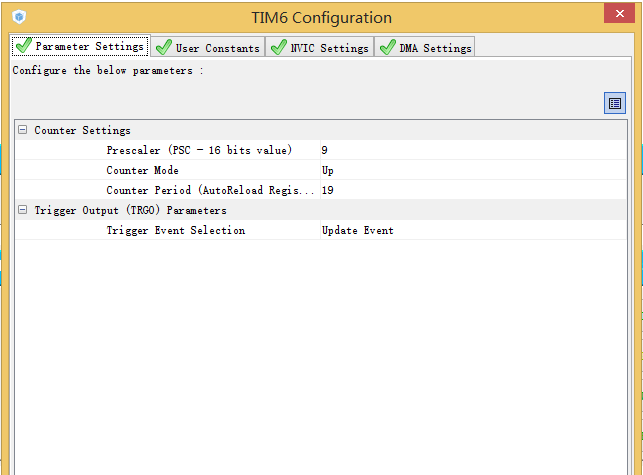
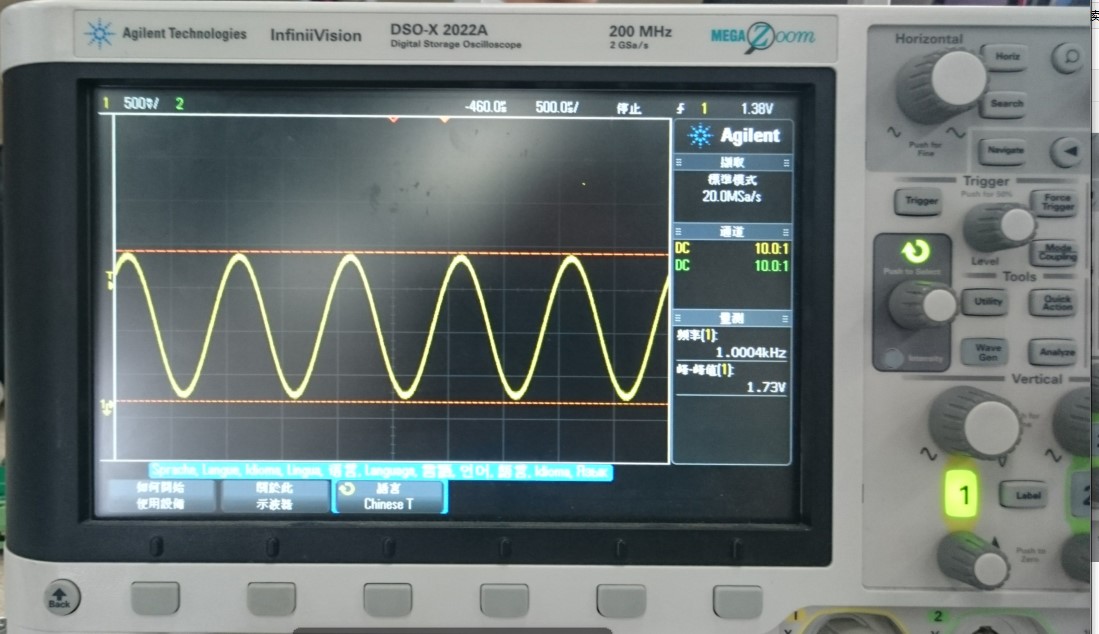
附件列表
基于STM32Cube的DAC数模转化的更多相关文章
- Python数模笔记-NetworkX(3)条件最短路径
1.带有条件约束的最短路径问题 最短路径问题是图论中求两个顶点之间的最短路径问题,通常是求最短加权路径. 条件最短路径,指带有约束条件.限制条件的最短路径.例如,顶点约束,包括必经点或禁止点的限制:边 ...
- Python数模笔记-Sklearn(1) 介绍
1.SKlearn 是什么 Sklearn(全称 SciKit-Learn),是基于 Python 语言的机器学习工具包. Sklearn 主要用Python编写,建立在 Numpy.Scipy.Pa ...
- Python数模笔记-(1)NetworkX 图的操作
1.NetworkX 图论与网络工具包 NetworkX 是基于 Python 语言的图论与复杂网络工具包,用于创建.操作和研究复杂网络的结构.动力学和功能. NetworkX 可以以标准和非标准的数 ...
- Python数模笔记-StatsModels 统计回归(4)可视化
1.如何认识可视化? 图形总是比数据更加醒目.直观.解决统计回归问题,无论在分析问题的过程中,还是在结果的呈现和发表时,都需要可视化工具的帮助和支持. 需要指出的是,虽然不同绘图工具包的功能.效果会有 ...
- Python数模笔记-Scipy库(1)线性规划问题
1.最优化问题建模 最优化问题的三要素是决策变量.目标函数和约束条件. (1)分析影响结果的因素是什么,确定决策变量 (2)决策变量与优化目标的关系是什么,确定目标函数 (3)决策变量所受的限制条件是 ...
- Python小白的数学建模课-A3.12 个新冠疫情数模竞赛赛题与点评
新冠疫情深刻和全面地影响着社会和生活,已经成为数学建模竞赛的背景帝. 本文收集了与新冠疫情相关的的数学建模竞赛赛题,供大家参考,欢迎收藏关注. 『Python小白的数学建模课 @ Youcans』带你 ...
- 当Python与数模相遇
数模有一个题目要处理杭州自行车在每个站点可用数量和已经借出数量,这数据在www.hzbus.cn上可以获取,它是10分钟更新一次的.这些数据手动获取,需要不停的刷页面,从6:00am到9:00pm,显 ...
- Python数模笔记-StatsModels 统计回归(1)简介
1.关于 StatsModels statsmodels(http://www.statsmodels.org)是一个Python库,用于拟合多种统计模型,执行统计测试以及数据探索和可视化. 2.文档 ...
- 基于STM32Cube的ADC模数采样设计
1.背景 此实验建立在STM32F429核心板基础上,对于深刻了解STM32Cube使用具有深刻意义.利用DMA进行ADC采样,具有速度快,极大减少CPU消耗的优势,对于数据采集系统具 ...
随机推荐
- 如何解决Maple的应用在数学中
对任意数学和技术学科的研究员.教师和学生而言,Maple是一个必备的工具.通过Maple,教师将复杂数学问题注入生命,学生的精力集中在概念理解上而不是如何使用工具上,研究员可以开发更复杂的算法或模型. ...
- For循环打印正三角,倒三角,菱形
A:正三角形: 内循环的判断条件:y<=x for(int x=0; x<5; x++) { for(int y=0; y<=x; y++) { System.out.print(& ...
- PHPCMS与UCenter整合要点
要点一: PHPCMS不能直接与UCenter整合,而是要经过 PHPSSO 适配,因此应用主URL应是 http://phpcms_url/phpsso_server 这种模式的. 要点二: 因为 ...
- PHP Strict Standards:问题解决
异常信息: ( ! ) Strict standards: Declaration of SugarEmailAddress::save() should be compatible with tha ...
- MySQL 数据库主从复制架构
前文<MySQL 数据库事务与复制>分析了 MySQL 复制过程中如何保证 binlog 和事务数据之间的一致性,本文进一步分析引入从库后需要保证主从的数据一致性需要考虑哪些方面. 原生复 ...
- 《Entity Framework 6 Recipes》中文翻译系列 (32) ------ 第六章 继承与建模高级应用之TPH与TPT (1)
翻译的初衷以及为什么选择<Entity Framework 6 Recipes>来学习,请看本系列开篇 6-6 映射派生类中的NULL条件 问题 你的表中,有一列允许为null.你想使用 ...
- 简单了解JS 中的indexOf方法
indexOf() 方法返回指定值在字符串对象中首次出现的位置.从 fromIndex 位置开始查找,如果不存在,则返回 -1. 首先先看下MDN下的参考文档,文档里列出的很详细,这里我只列出了注意点 ...
- Web APi之过滤器创建过程原理解析【一】(十)
前言 Web API的简单流程就是从请求到执行到Action并最终作出响应,但是在这个过程有一把[筛子],那就是过滤器Filter,在从请求到Action这整个流程中使用Filter来进行相应的处理从 ...
- 用js实现放大镜的效果
第一次发博客,还有点小激动,本人现在正在天津上大学,希望以后从事前端这一行业,学习的时间不长,写博客为了记录自己的学习过程和收获,当然也算是巩固.可能写的东西不会像大牛那样高大上,只是一些基本的内容, ...
- gsoap设置超时
1.修改gsoap自动生成的代码才能进行超时设置(我这边访问web service的代码都是gsoap工具自动生成.根据wsdl接口) 2.找到生成的soapwwwsdlBindingProxy.cp ...
