Uvaoj 10048 - Audiophobia（Floyd算法变形）

 
 1 /*
    题目大意：
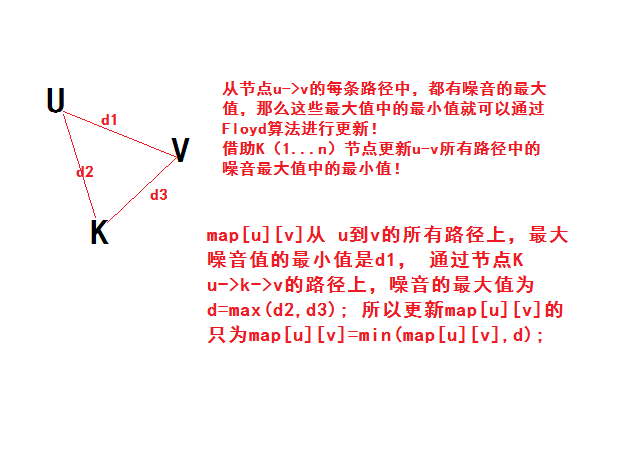
       从一个点到达另一个点有多条路径，求这多条路经中最大噪音值的最小值！ 、

    思路：最多有100个点，然后又是多次查询，想都不用想，Floyd算法走起！
 */
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #define INF 0x3f3f3f3f
 using namespace std;

 int map[][];

 int main(){
    int n, m, q;
    int u, v, d;
    int cnt=;
    scanf("%d%d%d", &n, &m, &q);
    while((n || m || q)){
          memset(map, 0x3f, sizeof(map));
       while(m--){
          scanf("%d%d%d", &u, &v, &d);
          map[u][v]=map[v][u]=d;
       }
       for(int k=; k<=n; ++k)
          for(int i=; i<=n; ++i)
            for(int j=; j<=n; ++j){
              int dd=max(map[k][j], map[i][k]);
              if(map[i][j] > dd)
                 map[i][j] = dd;
            }
       printf("Case #%d\n", ++cnt);
       while(q--){
          scanf("%d%d", &u, &v);
          if(map[u][v]==INF)
             printf("no path\n");
          else
             printf("%d\n", map[u][v]);
       }
       scanf("%d%d%d", &n, &m, &q);
       if((n || m || q))
          printf("\n");
    }
    return ;
 }