Codeforces1379-题解
很久以前,申蛤申请了一个cf号叫 wzxakioi
有一天,戌蛤带着申蛤用这个账号打了一场div3,然后它的rating超过了shzr
之后申蛤又用这个号打了三场div2,于是


CF1379C
题意:有一些礼物,当你第一次买第i个的时候会获得$a_i$的快乐值,之后每个会获得$b_i$的快乐值,问买n个最大快乐值$n\leq 1e9$
可以看出来的是如果已经确定了会买礼物的集合的话除了b最大的那个其余每种都只会买一个
枚举会买到b的那种礼物,如果其他礼物的a比这个b大就一定会买
所以把所有a和b都拿出来拍个序按顺序买
CF1379D
这道题除了题目很长没什么意思= =
题意:有一个车站,在一些时刻有货车需要离站。现在要每半小时发一辆客车,发客车前需要k min的时间使乘客上车,乘客上车时货车不能发车。问最少取消多少货车。
对于每个货车可以轻松求出在哪段时间发客车会使他无法正常运行,把这些都差分下来排个序,找到前缀和最小的位置就是答案。
考试时写到这里就只剩20min了,所以后面目前都是口胡
CF1379E
题意:找到一个n个点的二叉树,有m个点它的两个子树大小一个是另一个的两倍。
看起来可以找找规律,比如贡献最大的是毛毛虫,比如只有$2^k-1$这样的可以做到子树没有答案贡献,但是这样好像不能有1个贡献。其余情况可以做到一个贡献?
验证可行性以后dfs建树?
CF1379F
题意:有一个$2n\times 2m$的棋盘。对于$x+y$是偶数的位置可以放棋子。有一些位置可能会不能放棋子或恢复。问每次操作后能不能放nm个棋子。
把2*2的棋盘当成一格,一格内显然只能放一个棋子。所以需要每格内都能放一个棋子。
 出现这种情况肯定就没解了,然后这种好像还有传递性,也就是说
出现这种情况肯定就没解了,然后这种好像还有传递性,也就是说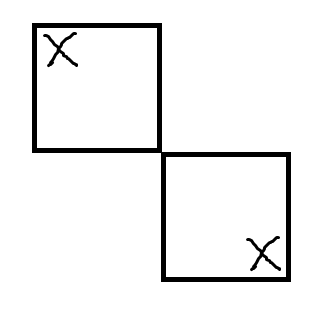 甚至
甚至 都没有解
都没有解
F1没有恢复操作可以直接二分check
F2就线段树分治嘛!但是题解好像是一个log的,等会儿再学习一下
Codeforces1379-题解的更多相关文章
- 2016 华南师大ACM校赛 SCNUCPC 非官方题解
我要举报本次校赛出题人的消极出题!!! 官方题解请戳:http://3.scnuacm2015.sinaapp.com/?p=89(其实就是一堆代码没有题解) A. 树链剖分数据结构板题 题目大意:我 ...
- noip2016十连测题解
以下代码为了阅读方便,省去以下头文件: #include <iostream> #include <stdio.h> #include <math.h> #incl ...
- BZOJ-2561-最小生成树 题解(最小割)
2561: 最小生成树(题解) Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 1628 Solved: 786 传送门:http://www.lyd ...
- Codeforces Round #353 (Div. 2) ABCDE 题解 python
Problems # Name A Infinite Sequence standard input/output 1 s, 256 MB x3509 B Restoring P ...
- 哈尔滨理工大学ACM全国邀请赛(网络同步赛)题解
题目链接 提交连接:http://acm-software.hrbust.edu.cn/problemset.php?page=5 1470-1482 只做出来四道比较水的题目,还需要加强中等题的训练 ...
- 2016ACM青岛区域赛题解
A.Relic Discovery_hdu5982 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Jav ...
- poj1399 hoj1037 Direct Visibility 题解 (宽搜)
http://poj.org/problem?id=1399 http://acm.hit.edu.cn/hoj/problem/view?id=1037 题意: 在一个最多200*200的minec ...
- 网络流n题 题解
学会了网络流,就经常闲的没事儿刷网络流--于是乎来一发题解. 1. COGS2093 花园的守护之神 题意:给定一个带权无向图,问至少删除多少条边才能使得s-t最短路的长度变长. 用Dijkstra或 ...
- CF100965C题解..
求方程 \[ \begin{array}\\ \sum_{i=1}^n x_i & \equiv & a_1 \pmod{p} \\ \sum_{i=1}^n x_i^2 & ...
- JSOI2016R3 瞎BB题解
题意请看absi大爷的blog http://absi2011.is-programmer.com/posts/200920.html http://absi2011.is-programmer.co ...
随机推荐
- <前端 js 实现 代码雨 >
前端 js 实现 代码雨: <!DOCTYPE html> <html lang="en"> <head> <meta charset= ...
- redis高级命令1
设置name的过期时间是20秒 redis默认是16个数据库,默认是将数据存储在第0个数据库中 因为默认是0,当你选择其他数据的时候,是没有值的
- Jmeter系列(30)- 详解 JDBC Request
如果你想从头学习Jmeter,可以看看这个系列的文章哦 https://www.cnblogs.com/poloyy/category/1746599.html 前言 JDBC Request 主要是 ...
- SQLSTATE[42000]: Syntax error or access violation: 1253 COLLATION 'utf8mb4_unicode_ci' is not valid for CHARACTER SET 'binary'
SQLSTATE[42000]: Syntax error or access violation: 1253 COLLATION 'utf8mb4_unicode_ci' is not valid ...
- Flask04-SQL
from flask import render_template, flash, redirect from app import app from app import db, models fr ...
- vs code 初始化vue项目框架
1.首先安装npm组件 下载地址:https://nodejs.org/en/ 安装完 2.配置环境变量 3.验证是否成功 node -v npm -v 4.替换npm 输入npm install ...
- 听说你还不知道CompletableFuture?
java8已经在日常开发编码中非常普遍了,掌握运用好它可以在开发中运用几行精简代码就可以完成所需功能.今天将介绍CompletableFuture的在生产环境如何使用实践.CompletableFut ...
- 轻松让HTML5可以显示桌面通知Notification非常实用
使用Notification的流程 1.检查浏览器是否支持Notification2.检查浏览器的通知权限3.如果权限不够则申请获取权限4.创建消息通知5.展示消息通知 Notification AP ...
- ExecutorsService 中的 submit和 execute的区别
闲来无事,写点代码练练手.于是就看了下ExecutorService常用的提交任务的方法: <T> Future<T> submit(Callable<T> tas ...
- Web移动端 自适应缩放界面
在开发App端的网页时,要适配iphone.ipad.ipod.安卓等各种机型,一般是直接使用em.px转em.界面缩放. 本章是通过将界面缩放,等比例显示在各机型上.过程中遇到了些问题和大坑~ 然后 ...
