【笔记】「pj复习」深搜——拿部分分

说在最前面

众所周知， NOIP pj 的第三题大部分都是 dp ，但是有可能在考场上想不到动态转移方程，所以我们就可以拿深搜骗分。

方法

1. 深搜拿部分分
   • 剪枝
   • 记忆化
2. 看数据范围

有时候发现，写完深搜，发现可以打表qwq！

那不就很香嘛（

实践出真知

例一：P1057 传球游戏

\(\Large\rm Link\)

法1

dfs 暴搜

期望得分：\(\rm 40pts\)

首先写出 \(dfs\) 的参数：

首先是小蛮在第几号，当然是 \(1\) ，然后是次数 \(0\)

再看递归边界

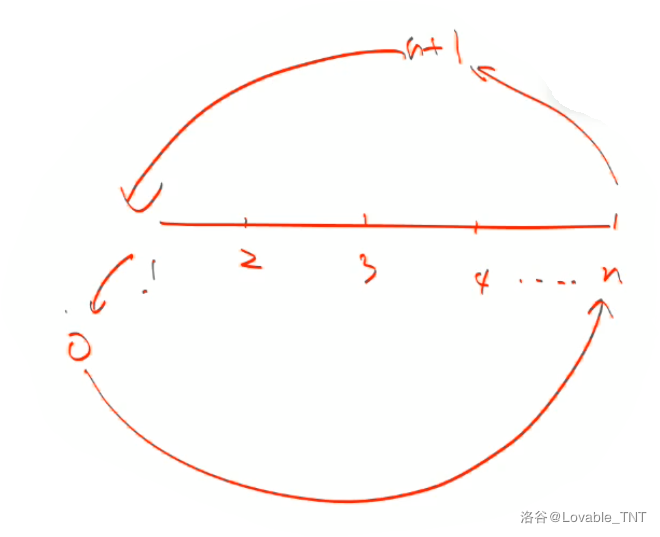
这里是环状递归边界：

if (x == 0) x = n;
if (x == n + 1) x = 1;
if (step == m) {
	if (x == 1) return 1;
    return 0;
}

接下来往下继续搜。

dfs(x + 1, step + 1) + dfs(x - 1, step + 1);

好！ \(\rm 40pts\) 到手！

那么我们可以再看一下数据范围，那么小！直接打表啊！

因为时间关系，这里打表就不多讲解了。

法2

加上记忆化

期望得分：\(\rm 90pts\)

大家应该都知道：暴搜加上记忆化 \(≈\) 动归

所以我们加上记忆化：

定义一个 \(a\) 数组，表示在某一个位置经过 \(step\) 步能否回到起始位置的方法数。

if (a[x][step] != 0) return a[x][step];

放上 dfs 代码：

int dfs (int x, int step) {
	if (x == 0) x = n;
	if (x == n + 1) x = 1;
	if (step == m) {
		if (x == 1) return 1;
	    return 0;
	}
	return dfs(x + 1, step + 1) + dfs(x - 1, step + 1);
}

为什么是 90 分？？？

因为想一下，如果是奇数，那么永远传不到小蛮手中，就会肯定 T 。

法3

加一个特判。

期望得分： \(100pts\)

    if (n % 2 == 0 && m % 2 == 1) {
		cout << 0;
		return 0;
	}

法4

既然这题的正解是 dp，那么我们还是要讲讲 dp 的。

其实 dp 和记忆化没有很大的区别。

状态表示：\(\rm f[i][j]\) 表示第 \(i\) 次传球后球在第 \(j\) 个小朋友手上回到小蛮手中的方案数。

我们发现 \(\rm f[i][j]\) 跟 \(\rm a[x][step]\) 是很像的。

状态转移：\(\rm f[i][j] =
\begin{cases}
\rm f[i - 1][j - 1] & \text{第 i 次传球从左边传给 j}\\
\rm f[i - 1][j + 1] & \text{第 i 次传球从右边传给 j}
\end{cases}\)

这样写对不对？不对！

因为这是环状的，环状的解决方法通常是 \(\mod n\)

\((x + n - 1) \mod n + 1\)

所以正确状态转移为：\(\rm f[i][j] =
\begin{cases}
\rm f[i - 1][(j - 1 + n - 1) \mod n + 1] & \text{第 i 次传球从左边传给 j}\\
\rm f[i - 1][(j + 1 + n - 1) \mod n + 1] & \text{第 i 次传球从右边传给 j}
\end{cases}\)

所以：\(\rm f[i][j] = f[i - 1][(j - 1 + n - 1) \mod n + 1] + f[i - 1][(j + 1 + n - 1) \mod n + 1]\)

做完，最后放上 AC 代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<string>
#define line cout << endl
using namespace std;
int f[35][35];
int n, m;
int main() {
	cin >> n >> m;
	f[1][n] = f[1][2] = 1;
	for (int i = 2; i <= m; i++) {
		for (int j = 1; j <= n; j++) {
			f[i][j] = f[i - 1][(j - 1 + n - 1) % n + 1] + f[i - 1][(j + 1 + n - 1) % n + 1];
		}
	}
	cout << f[m][1] << endl;
	return 0;
}