【poj 1182】食物链（图论--带权并查集）

题意：有3种动物A、B、C，形成一个“A吃B， B吃C，C吃A ”的食物链。有一个人对N只这3类的动物有M种说法：第一种说法是"1 X Y"，表示X和Y是同类。；第二种说法是"2 X Y"，表示X吃Y。假设输入为（d,X,Y）。可知，当一句话满足下列三条之一时，这句话就是假话，否则就是真话。 

1） 当前的话与前面的某些真的话冲突，就是假话； 

2） 当前的话中X或Y比N大，就是假话； 

3） 当前的话表示X吃X，就是假话。
要求输出假话的总数。

解法：带权并查集。同【bzoj 1202】[HNOI2005] 狡猾的商人（图论--带权并查集+前缀和）类似，判断假话的条件一就是要与之前得到的结果冲突。所以推断出用并查集的原因：绝对不是因为有3“种”动物，而是因为这个“之前有结果就判断，没有结果就存储”的操作。

于是由于已经知道要用并查集，就需要推出树上结点的关系，使f[x]表示动物x与其所在联盟的根节点R的关系（x→R）。再通过枚举的方法，列举出所有情况，得出规律。再应用到具体的函数等操作中。

QUESTION!!!(这里理应大写加粗~)  OMG!!!∑(ﾟДﾟノ)ノ我突然间发现若用“方块图”，我下面的所有推导都显得无比无比的复杂啊！直接转换x→y（定义x下y上）的关系为：x到y的距离 或 x上面方块的个数，所有的都可以一步写出来呀！有神牛告诉我带权并查集都是可以这样理解的吗？！！！！所有的找父亲结点并更新自己的find(x)函数那里，f[x]都是f[x]+f[fx]吗。。。

推导过程如下：如图1所示，设x,y分别是R的子结点；如图2所示，x→R表示x吃R，相应数字。0为x,R同类，1为x吃R，2为R吃x；具体对应情况枚举如图3所示。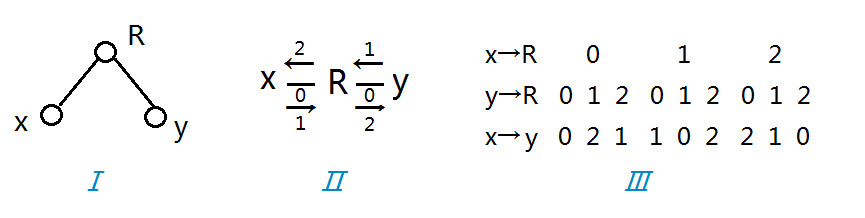
于是据图3找规律，相加不行便相减，发现(第一行数-第二行数+3)%3=第三行数，即(f[x]-f[y]+3)%3=d-1。（d为输入中x,y的关系种类）

因此，根据这一条树上的规律，我们就可以把它应用到所有函数中了。具体请见代码——

 1 #include<cstdio>
 2 #include<cstdlib>
 3 #include<cstring>
 4 #include<iostream>
 5 using namespace std;
 6
 7 const int N=50010,M=100010;
 8 int fa[N],f[N];
 9 int n,m;
10
11 int ffind(int x)
12 {
13     if (fa[x]!=x)
14     {
15       int fx=fa[x];
16       fa[x]=ffind(fx);
17       /*推导：
18       f[x]=(f[x]-f[fa[x]]+3)%3;
19           =(f[x]-((3-f[fx])%3)+3)%3;
20       */
21       f[x]=(f[x]+f[fx])%3;
22     }
23     return fa[x];
24 }
25 int main()
26 {
27     scanf("%d%d",&n,&m);
28     int cnt=0;
29     for (int i=1;i<=n;i++) fa[i]=i,f[i]=0;
30     for (int i=1;i<=m;i++)
31     {
32       int d,x,y;
33       scanf("%d%d%d",&d,&x,&y);
34       if (x>n||y>n||(d==2&&x==y)) {cnt++;continue;}
35       d--;//
36       int fx=ffind(x),fy=ffind(y);
37       if (fx!=fy)
38       {
39         fa[fx]=fy;
40         /*推导：
41         int t=(3-f[x])%3;//fx->x
42         int tt=(3-d)%3;//y->x
43         int w=(t-tt+3)%3;//fx->y
44         int ww=(3-f[y])%3;//fy->y
45         f[fx]=(w-ww+3)%3;//fx->fy
46         */
47         f[fx]=(f[y]-f[x]+d+3)%3;
48       }
49       else if ((f[x]-f[y]+3)%3!=d) cnt++;
50     }
51     printf("%d\n",cnt);
52     return 0;
53 }

--------------------------------------------------------------------------------------------------------------------------------

另外啊~我学习了一下好友的做法：x->y间的边权直接看成距离，1为x吃y，0为同类。这样一个食物链的x,y,z的关系都可直接推出！！○|￣|_  orz~
还有，合并父亲时，可以让y变为fx的父亲，而不是fy变为fx的父亲，这样虽然增大了树的深度，但影响不大，重要的是可以节省一些代码。