力扣224(java)-基本计算器（困难）

题目：

给你一个字符串表达式 s ，请你实现一个基本计算器来计算并返回它的值。

注意:不允许使用任何将字符串作为数学表达式计算的内置函数，比如 eval() 。

示例 1：

输入：s = "1 + 1"
输出：2
示例 2：

输入：s = " 2-1 + 2 "
输出：3
示例 3：

输入：s = "(1+(4+5+2)-3)+(6+8)"
输出：23

提示：

• 1 <= s.length <= 3 * 105
• s 由数字、'+'、'-'、'('、')'、和 ' ' 组成
• s 表示一个有效的表达式
• '+' 不能用作一元运算(例如， "+1" 和 "+(2 + 3)" 无效)
• '-' 可以用作一元运算(即 "-1" 和 "-(2 + 3)" 是有效的)
• 输入中不存在两个连续的操作符
• 每个数字和运行的计算将适合于一个有符号的 32位 整数

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/basic-calculator
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路：

这道题对于现在的我还挺困难的参考三叶姐@宫水三叶的题解，梳理一下这道题的思路

利用双栈来解决：

• 使用栈nums:来存放所有的操作数
• 使用栈ops：来存放所有的操作符

将s中所有的空格去掉，并转换成字符数组，然后从前往后遍历字符，根据遇到的字符来分情况讨论:

• 遇到左括号 ( :就将其加入到ops中，等待与之匹配的右括号 );
• 遇到右括号  )：ops中操作符不为空时，就将栈中已有操作数和操作符进行计算，将计算结果放进nums中，直到遇到与之匹配的最近的左括号停止，弹出左括号；
• 遇到整数：将当前位置开始的连续整数取出，放入nums中；
• 有新的操作符入栈时，先将栈中已有同等级的操作符和操作数进行计算，计算结果放入nums，直到操作符为空或者遇到左括号时，再入栈，后续再进行计算剩下的。

注意点：

1.第一个数可能为负数（-6）：这样第一个操作符可能被认为 '减号',计算时没有前面的数与之计算，可以再最开始就加入一个0，变成 0-6这样结果也正好为-6;

2.为了防止括号内出现的首个字符为运算符，将 (- 替换成 ( 0-， (+ 替换成 (0+。

代码：

 1 class Solution {
 2     public int calculate(String s) {
 3         //定义两个栈，一个用来存放操作数，一个用来存放操作符
 4         Deque<Integer> nums = new ArrayDeque<>();
 5         Deque<Character> ops = new ArrayDeque<>();
 6         //为了防止第一个数出现负数,先将操作数栈中加入0
 7         nums.addLast(0);
 8         //将空格去掉
 9         s = s.replaceAll(" ", "");
10         //将s转换成一个字符数组
11         char[] cs = s.toCharArray();
12         int n = cs.length;
13         for(int i = 0; i < n; i++){
14             char c = cs[i];
15             //如果遇到左括号，就将操作符加入栈中
16             if(c == '('){
17                 ops.addLast(c);
18             }else if(c == ')'){
19                 while(!ops.isEmpty()){
20                     char op = ops.peekLast();
21                     //如果不是左括号，就将括号内的数和操作符进行计算
22                     if(op != '('){
23                         calc(nums, ops);
24                     }else{
25                         //如果是左括号，就将左括号弹出
26                         ops.pollLast();
27                         break;
28                     }
29                 }
30             }else{
31                 if(isNum(c)){
32                     //定义当前整数
33                     int num = 0;
34                     int j = i;
35                     //从i位开始后面的连续数字整体取出，加入到栈nums中
36                     while(j < n && isNum(cs[j])){
37                         num = num * 10 + (int)(cs[j++] - '0');
38                     }
39                     nums.addLast(num);
40                     i = j - 1;
41                 }else{
42                     //将（-和(+  替换成 (0-和(0+
43                     if(i > 0 && (cs[i-1] == '(' || cs[i-1] == '+' || cs[i-1] == '-')){
44                         nums.addLast(0);
45                     }
46                     //有新操作符入栈，先把栈内元素算出，直到没有操作符或遇到左括号，再入栈
47                     while(!ops.isEmpty() && ops.peekLast() != '('){
48                         calc(nums, ops);
49                     }
50                     ops.addLast(c);
51                 }
52             }
53         }
54             //算剩下的
55         while(!ops.isEmpty()){
56             calc(nums, ops);
57         }
58         return nums.peekLast();
59     }
60
61
62         //定义一个方法用于计算
63         void calc(Deque<Integer> nums, Deque<Character> ops){
64             //如果操作数不足以及无操作符，则无法计算
65             if(nums.isEmpty() || nums.size() < 2) return;
66             if(ops.isEmpty()) return;
67             //取出栈顶元素和操作符进行计算
68             int b = nums.pollLast(), a = nums.pollLast();
69             char op = ops.pollLast();
70             nums.addLast(op == '+' ? a+b : a-b);
71         }
72         //判断字符是否为数字
73         boolean isNum(char c){
74             return Character.isDigit(c);
75         }
76     }

一些注解：

 1 if(isNum(c)){
 2     //定义当前整数
 3      int num = 0;
 4      int j = i;
 5     //从i位开始后面的连续数字整体取出，加入到栈nums中
 6       while(j < n && isNum(cs[j])){
 7          num = num * 10 + (int)(cs[j++] - '0');
 8        }
 9       nums.addLast(num);
10       i = j - 1;

• num = num * 10 + (int)(cs[j++] - '0')：就像取出像23,569这种超过一位数的整数；
• i = j - 1：例如 56+,i从0开始（利用另一个变量j这里来替换一下i），当i为2时就已经不是数字了，整个for循环就结束了，for循环中就会i++,i == 3,就会跳过56后面的加号，所以if这里面就会将i回退一个指向6,后面for循环i++就会刚好到加号的位置。

1   //将（-和(+  替换成 (0-和(0+
2  if(i > 0 && (cs[i-1] == '(' || cs[i-1] == '+' || cs[i-1] == '-')){
3        nums.addLast(0);
4 }

为了规避一些 ‘不合法的计算表达式’，例如 (+5-6) 变成 (0+5-6)

小知识：

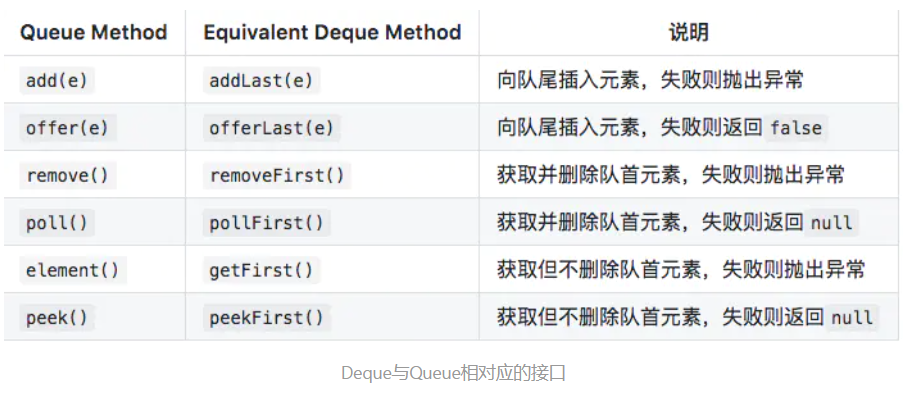
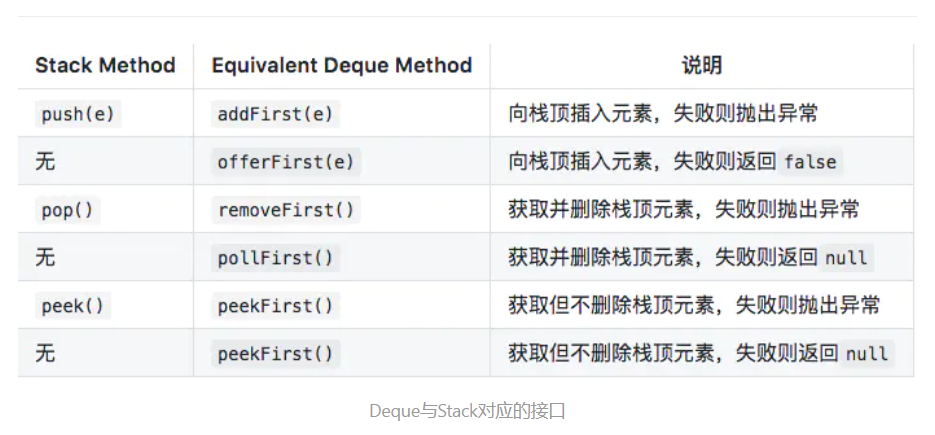
Deque双端队列这种数据结构很灵活，即可以满足队列的FIFO(先进先出)特性，又可以满足栈的LIFO(后进先出)特性，那么分别作为队列和栈，Deque类常用的方法：