Life Winner Bo HDU - 5754

Bo is a "Life Winner".He likes playing chessboard games with his girlfriend G. 

The size of the chessboard is N×MN×M.The top left corner is numbered(,)(,) and the lower right corner is numberd (N,M)(N,M). 

For each game,Bo and G take turns moving a chesspiece(Bo first).At first,the chesspiece is located at (,)(,).And the winner is the person who first moves the chesspiece to (N,M)(N,M).At one point,if the chess can't be moved and it isn't located at (N,M)(N,M),they end in a draw. 

In general,the chesspiece can only be moved right or down.Formally,suppose it is located at (x,y)(x,y),it can be moved to the next point (x′,y′)(x′,y′) only if x′≥xx′≥x and y′≥yy′≥y.Also it can't be moved to the outside of chessboard. 

Besides,There are four kinds of chess(They have movement rules respectively). 

.king. 

.rook(castle). 

.knight. 

.queen. 

(The movement rule is as same as the chess.) 

For each type of chess,you should find out that who will win the game if they both play in an optimal strategy. 

Print the winner's name("B" or "G") or "D" if nobody wins the game.
Input
In the first line,there is a number TT as a case number. 

In the next TT lines,there are three numbers type,NN and MM. 

"type" means the kind of the chess. 

T≤,≤N,M≤,≤type≤4T≤,≤N,M≤,≤type≤
Output
For each question,print the answer.
Sample Input

Sample Output
G
G
D
B

Problem Description

以下解释参考：

https://blog.csdn.net/xtulollipop/article/details/52046874

https://www.cnblogs.com/Ritchie/p/5708601.html

我也看了老半天，真是渣渣

问给一种棋子，两人轮流走，只能向右或下下走，最后到N,M的赢。
1、王（King）：横、直、斜都可以走，但每次限走一步
2、车（Rook）：横、竖均可走，不能斜走，格数不受限制，除王车易位的情况下，平时不能越子
3、马（Knight）：每步棋先横走或竖走一格，再斜走一格（或者横两格竖一格，竖两格横一格），可以越子
4、后（Queen）：横、竖、斜都可以走，格数不受限制，但不能越子

1.王   拿SG预处理一下

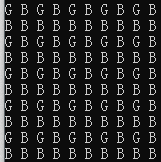
你也可以找出规律发现：当n和m全为奇数时，先手必败。

2.车   到达终点时总要走n行，m列。可以把他们看成Nim的两堆石子。Nim游戏 ，异或一下

3.马   因为我们只考虑必胜必败态，其他的可能赢或输的点，我总是不走过去，会使得这个是平局。。打表

观察图表：先n--，m--，把问题转化为(0,0)是终点，如果n+m不是3的倍数一定是平局；如果是3的倍数，如果nm相等，那么一定是必败的，先手减2减1，后手就减1减2，必败；如果nm不等且n=m+1或者m=n+1，那么先手必胜，因为可以一步走到必败点，必胜；其余情况都是平局，因为如果一方存在赢的情况，另一方可以不走那步，把小的数-2，大的数-1，往墙上靠，谁也赢不了肯定是平局。

4.后   和车一样考虑，就是可以拿任意堆任意个，或者拿两堆同时拿任意个，是一个标准的威佐夫博弈

AC Code：

1.

#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;

bool SG[][];
int SG3[][];
int a,n,m;

bool visit[];
void getSG1(){
    memset(SG,,sizeof(SG));
    for(int i=;i<=;i++){
        for(int j=;j<=;j++){
            memset(visit,,sizeof(visit));
            if(i->) visit[SG[i-][j]]=true;
            if(j->) visit[SG[i][j-]]=true;
            if(i->&&j->)visit[SG[i-][j-]]=true;
            for(int k=;;k++){
                if(visit[k]==){
                    SG[i][j]=k;
                    break;
                }
            }
        }
    }
}
void getSG3(){
    memset(SG3,-,sizeof(SG3));
    SG3[][]=;
    for(int i=;i<=;i=i+){
        SG3[i][i]=;
        SG3[i-][i-]=;
        SG3[i-][i-]=;
    }
}
int main(){
    int t;
    scanf("%d",&t);
    getSG1();
    getSG3();
    while(t--){
       scanf("%d %d %d",&a,&n,&m);
       if(n>m) swap(n,m);
       if(a==){
            if(SG[n][m]) printf("B\n");
            else printf("G\n");
       }
       else if(a==){
            if((n^m)) printf("B\n");
            else printf("G\n");
       }
       else if(a==){
            if(SG3[n][m]==) printf("B\n");
            else if(SG3[n][m]==-)printf("D\n");
            else printf("G\n");
       }
       else if(a==){
            n--;
            m--;
            if(n<m) swap(n,m);
            int k=n-m;
            n=(int)(k*(+sqrt())/2.0);
            if(n==m) printf("G\n");
            else printf("B\n");
       }
    }
    return ;
}

2.

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
int t,a,b,c;
void pra()
{
    puts("B");
}
void prb()
{
    puts("G");
}
void prc()
{
    puts("D");
}
void solve1()
{
    if((a&)&&(b&))
    prb();
    else
    pra();
}
void solve2()
{
    if((a^b)!=) pra();
    else prb();
}
void solve3()
{
    a--;
    b--;
    if((a+b)%!=)
    prc();
    else
    {
        if(a<b) swap(a,b);
        if(a==b) prb();
        else if((a-b)==) pra(); //()
        else prc();
    }
}
void solve4()
{
    a--;
    b--;
    if(a>b)
    swap(a,b);
    c=b-a;
    if(a==int((sqrt()+)/*c))
    prb();
    else
    pra();
}
int main()
{
    cin>>t;
    while(t--)
    {
        cin>>c>>a>>b;
        if(c==) solve1();
        else if(c==) solve2();
        else if(c==) solve3();
        else if(c==) solve4();
    }
    return ;
}