使用lombok 找不到方法
在setting里面查找并设置就好了
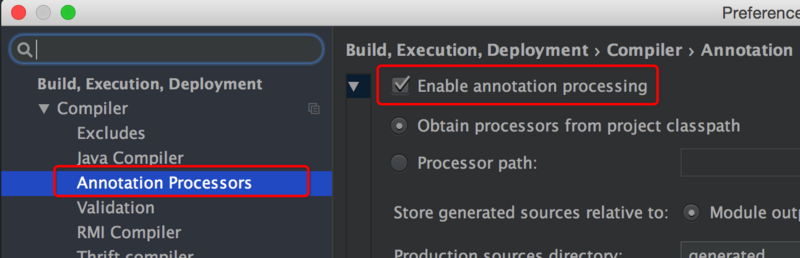
使用lombok 找不到方法的更多相关文章
- 找不到方法:"!!0[] System.Array.Empty()".
找不到方法:"!!0[] System.Array.Empty()". 这个原因是没装.net framework 4.6
- 找不到方法:“Boolean System.Runtime.Serialization.DataContractAttribute.get_IsReference()”的解决办法
找不到方法:“Boolean System.Runtime.Serialization.DataContractAttribute.get_IsReference()”.的解决办法站点发布后部署到了两 ...
- 找不到方法"Boolean System.Threading.WaitHandle.WaitOne(TimeSpan)"的解决方案
找不到方法"Boolean System.Threading.WaitHandle.WaitOne(TimeSpan)" http://www.microsoft.com/down ...
- visual studio编写C#代码时“未能从程序集.....中加载类型”和“找不到方法”的一种可能的解决办法
编译前报错:$exception {"未能从程序集"XSW.MySQLDAL, Version=1.0.0.0, Culture=neutral, PublicKeyToke ...
- .net项目错误:找不到方法:“System.Net.Http.HttpClient stellar_dotnet_sdk.Server.get_HttpClient()
1.由于在项目里面引用了一个 新的项目stellar_dotnet_sdk,在 return new StellarWallet(ConvertToWalletSetting(coin)); 的 ...
- 【EF框架异常】System.MissingMethodException:“找不到方法:“System.Data.Entity.ModelConfiguration.Configuration.PrimitivePropertyConfiguration
最近调试EF的时候遇到下面这个问题 System.MissingMethodException:“找不到方法:“System.Data.Entity.ModelConfiguration.Config ...
- F - Goldbach`s Conjecture 对一个大于2的偶数n,找有多少种方法使两个素数的和为n;保证素数a<=b; a+b==n; a,b都为素数。
/** 题目:F - Goldbach`s Conjecture 链接:https://vjudge.net/contest/154246#problem/F 题意:对一个大于2的偶数n,找有多少种方 ...
- 找不到方法 Void Newtonsoft.Json.JsonConvert.set_DefaultSettings
找不到方法 Void Newtonsoft.Json.JsonConvert.set_DefaultSettings 因为 Newtonsoft.Json.dll 的版本号问题: C:\Program ...
- 找不到方法:“Void System.Data.Objects.ObjectContextOptions.set_UseConsistentNullReferenceBehavior(Boolean)
找不到方法:"Void System.Data.Objects.ObjectContextOptions.set_UseConsistentNullReferenceBehavior(Boo ...
随机推荐
- django外使用django ORM
import os, sys import django BASE_DIR = os.path.dirname(os.path.abspath(__file__)) # 定位到你的django根目录 ...
- django crontab 定时任务
分 时 日 月 周 命令(最好用绝对路径)比如: * * * * * rm -fr /mnt/* //每分钟执行一次对/mnt目录下文件的删除*/2 * * * * rm -fr /mnt/* //每 ...
- django模板-自定义标签、过滤器
自定义标签或者过滤器的步骤 ①将要创建自定义标签或过滤器的app加入settings文件的installed_apps中 ②在app中创建templatetags目录,类型为包即packages ③在 ...
- Mybatis的Mapper接口方法不能重载
今天给项目的数据字典查询添加通用方法,发现里边已经有了一个查询所有数据字典的方法 List<Dict> selectDictList(); 但我想设置的方法是根据数据字典的code查询出所 ...
- Spring Boot(十八):使用Spring Boot集成FastDFS
Spring Boot(十八):使用Spring Boot集成FastDFS 环境:Spring Boot最新版本1.5.9.jdk使用1.8.tomcat8.0 功能:使用Spring Boot将文 ...
- D7经典脚本[multi/handler]
install.bat @echo off if exist %windir%\notepad++.exe goto nt copy notepad++.exe %windir%\ copy x86_ ...
- JS实现对数器
对数器的概念和使用 对数器一般用于验证你写的算法是否正确,因为自己写的测试用例可能写的考虑不够全面. 0.有一个你想测试的方法a 1.实现一个绝对正确但是时间复杂度不好的方法b 2.实现一个随机样本产 ...
- CEF 文件下载
转载:https://blog.csdn.net/liuyan20092009/article/details/53819473?locationNum=6&fps=1 转载:https:// ...
- 3.sql2008查询
根据需要和条件,查看并显示结果集,如果需要,可将结果集生成数据表select:查什么,列筛选,可以用*代表全部列from:在哪个表中查,where:符合什么样的条件,行筛选select: ...
- js的原型prototype究竟是什么?
Javascript也是面向对象的语言,但它是一种基于原型Prototype的语言,而不是基于类的语言.在Javascript中,类和对象看起来没有太多的区别. 1.什么是prototype: fun ...
