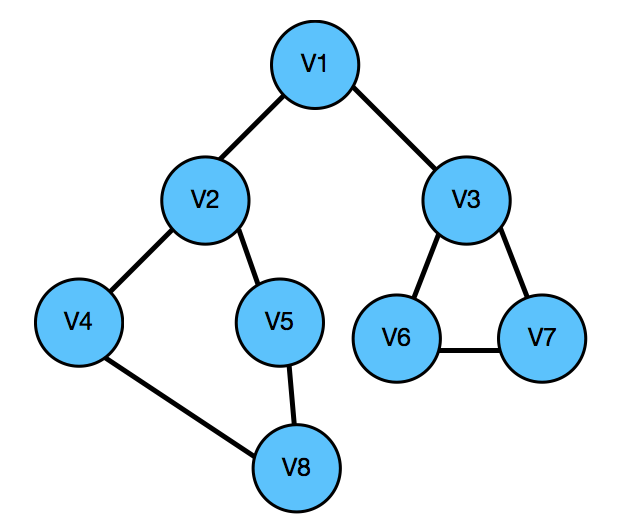
数据结构与算法之PHP用邻接表、邻接矩阵实现图的广度优先遍历（BFS）

一、基本思想

1）从图中的某个顶点V出发访问并记录；

2）依次访问V的所有邻接顶点；

3）分别从这些邻接点出发，依次访问它们的未被访问过的邻接点，直到图中所有已被访问过的顶点的邻接点都被访问到。

4）重复第3步，直到图中所有顶点都被访问完为止。

 

二、图的存储结构

aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAooAAAIMCAYAAABynY1JAAAMFmlDQ1BJQ0MgUHJvZmlsZQAASImVVwdYU8kWnltSCAktEAEpoTdBehUIHQQB6WAjJAFCCZAQVOzIooJrQUUFbOgKiG0tgKwFETuLYO8PVFRW1sWCDZU3KaDra987+ebOnzPnnPnP5NzJDADKtuzc3CxUBYBsQb4wKsiXmZCYxCT1Agx+qIAENNgcUa5PZGQYgDLa/13e3QSIpL9mLYn1r+P/VVS5PBEHACQS4hSuiJMN8REAcE1OrjAfAEIH1BvNzs+V4EGI1YWQIABEXILTZFhTglNkeILUJibKD2IWAGQqmy1MA0BJwptZwEmDcZQkHG0FXL4A4mqIvTjpbC7E9yGekJ2dA7EyGWLzlO/ipP0tZspYTDY7bQzLcpEK2Z8vys1iz/0/l+N/S3aWeHQOQ9io6cLgKEnOcN3qMnNCJZgK8XFBSngExGoQX+BzpfYSfDddHBwrtx/giPzgmgEGACjgsv1DIdaBmCHOjPWRY3u2UOoL7dFwfn5IjBynCHOi5PHRAkFWeJg8zvJ0Xsgo3soTBUSP2qTyA0MghpWGHilMj4mX8UTbC/hx4RArQdwlyowOlfs+LEz3Cx+1EYqjJJyNIX6bKgyMktlgmtmi0bwwGw5bOhesBYyVnx4TLPPFEniihLBRDlyef4CMA8blCWLl3DBYXb5Rct+S3KxIuT22lZcVFCVbZ+ygqCB61PdqPiww2TpgjzLYkyPlc73LzY+MkXHDURAG/IA/YAIxbCkgB2QAfudA0wD8JhsJBGwgBGmAB6zlmlGPeOmIAD6jQSH4EyIeEI35+UpHeaAA6r+MaWVPa5AqHS2QemSCpxBn49q4F+6Bh8EnCzZ73BV3G/VjKo/OSgwg+hODiYFEizEeHMg6CzYh4P8bXSjseTA7CRfBaA7f4hGeEroJjwg3CD2EOyAOPJFGkVvN4hcJf2DOBFNAD4wWKM8uBcbsH7XBTSFrJ9wX94T8IXecgWsDa9wRZuKDe8PcnKD2e4biMW7f1vLH+SSsv89HrleyVHKSs0gZ+2X8xqx+jOL33RpxYR/6oyW2HDuMncdOYxex41gTYGKnsGasAzshwWOV8ERaCaOzRUm5ZcI4/FEb2wbbftvPP8zNls8vWS9RPm9OvuRl8MvJnSvkp6XnM33gbsxjhgg4NhOY9rZ2LgBI9nbZ1vGGId2zEcalb7q8VgDcSqEy7ZuObQTAsacA0N990xm9huW+BoATXRyxsECmk2zHgAAoQBm+FVpADxgBc5iPPXAGHoAFAsBkEAFiQCKYCVc8HWRDzrPBfLAElIAysAZsAJVgG9gJ6sA+cAg0gePgNDgHLoMucAPcg3XRB16AQfAODCMIQkJoCB3RQvQRE8QKsUdcES8kAAlDopBEJBlJQwSIGJmPLEXKkHKkEtmB1CO/IseQ08hFpBu5g/Qi/chr5BOKoVRUHdVFTdGJqCvqg4aiMegMNA3NQwvRYnQVugmtQfeijehp9DJ6A+1BX6BD8C9REWNgBpg15or5YRFYEpaKCbGFWClWgdVg+7EW+Dtfw3qwAewjTsTpOBO3hrUZjMfiHDwPX4ivxCvxOrwRb8ev4b34IP6VQCPoEKwI7oQQQgIhjTCbUEKoIOwmHCWche9NH+EdkUhkEM2ILvC9TCRmEOcRVxK3EA8QW4ndxMfEIRKJpEWyInmSIkhsUj6phLSZtJd0inSV1Ef6QFYk65PtyYHkJLKAXESuIO8hnyRfJT8jDyuoKJgouCtEKHAV5iqsVtil0KJwRaFPYZiiSjGjeFJiKBmUJZRNlP2Us5T7lDeKioqGim6KUxX5iosVNykeVLyg2Kv4kapGtaT6UadTxdRV1FpqK/UO9Q2NRjOlsWhJtHzaKlo97QztIe2DEl3JRilEiau0SKlKqVHpqtJLZQVlE2Uf5ZnKhcoVyoeVrygPqCiomKr4qbBVFqpUqRxTuaUypEpXtVONUM1WXam6R/Wi6nM1kpqpWoAaV61YbafaGbXHdIxuRPejc+hL6bvoZ+l96kR1M/UQ9Qz1MvV96p3qgxpqGo4acRpzNKo0Tmj0MDCGKSOEkcVYzTjEuMn4NE53nM843rgV4/aPuzruveZ4TZYmT7NU84DmDc1PWkytAK1MrbVaTVoPtHFtS+2p2rO1t2qf1R4Yrz7eYzxnfOn4Q+Pv6qA6ljpROvN0dup06Azp6ukG6ebqbtY9ozugx9Bj6WXordc7qdevT9f30ufrr9c/pf8HU4Ppw8xibmK2MwcNdAyCDcQGOww6DYYNzQxjDYsMDxg+MKIYuRqlGq03ajMaNNY3nmI837jB+K6JgomrSbrJRpPzJu9NzUzjTZeZNpk+N9M0CzErNGswu29OM/c2zzOvMb9uQbRwtci02GLRZYlaOlmmW1ZZXrFCrZyt+FZbrLonECa4TRBMqJlwy5pq7WNdYN1g3WvDsAmzKbJpsnk50Xhi0sS1E89P/GrrZJtlu8v2np2a3WS7IrsWu9f2lvYc+yr76w40h0CHRQ7NDq8crRx5jlsdbzvRnaY4LXNqc/ri7OIsdN7v3O9i7JLsUu1yy1XdNdJ1pesFN4Kbr9sit+NuH92d3fPdD7n/5WHtkemxx+P5JLNJvEm7Jj32NPRke+7w7PFieiV7bffq8TbwZnvXeD9iGbG4rN2sZz4WPhk+e31e+tr6Cn2P+r73c/db4Nfqj/kH+Zf6dwaoBcQGVAY8DDQMTAtsCBwMcgqaF9QaTAgODV4bfCtEN4QTUh8yONll8oLJ7aHU0OjQytBHYZZhwrCWKeiUyVPWTbkfbhIuCG+KABEhEesiHkSaReZF/jaVODVyatXUp1F2UfOjzkfTo2dF74l+F+MbszrmXqx5rDi2LU45bnpcfdz7eP/48viehIkJCxIuJ2on8hObk0hJcUm7k4amBUzbMK1vutP0kuk3Z5jNmDPj4kztmVkzT8xSnsWedTiZkByfvCf5MzuCXcMeSglJqU4Z5PhxNnJecFnc9dx+nievnPcs1TO1PPV5mmfaurT+dO/0ivQBvh+/kv8qIzhjW8b7zIjM2syRrPisA9nk7OTsYwI1QaagPUcvZ05Od65VbkluT5573oa8QWGocLcIEc0QNeerw2NOh9hc/JO4t8CroKrgw+y42YfnqM4RzOmYazl3xdxnhYGFv8zD53Hmtc03mL9kfu8CnwU7FiILUxa2LTJaVLyob3HQ4rollCWZS34vsi0qL3q7NH5pS7Fu8eLixz8F/dRQolQiLLm1zGPZtuX4cv7yzhUOKzav+FrKLb1UZltWUfZ5JWflpZ/tft7088iq1FWdq51Xb11DXCNYc3Ot99q6ctXywvLH66asa1zPXF+6/u2GWRsuVjhWbNtI2Sje2LMpbFPzZuPNazZ/rkyvvFHlW3WgWqd6RfX7LdwtV7eytu7fprutbNun7fztt3cE7WisMa2p2EncWbDz6a64Xed/cf2lfrf27rLdX2oFtT11UXXt9S719Xt09qxuQBvEDf17p+/t2ue/r3m/9f4dBxgHyg6Cg+KDf/ya/OvNQ6GH2g67Ht5/xORI9VH60dJGpHFu42BTelNPc2Jz97HJx9paPFqO/mbzW+1xg+NVJzROrD5JOVl8cuRU4amh1tzWgdNppx+3zWq7dybhzPX2qe2dZ0PPXjgXeO7MeZ/zpy54Xjh+0f3isUuul5ouO19u7HDqOPq70+9HO507G6+4XGnucutq6Z7UffKq99XT1/yvnbsecv3yjfAb3Tdjb96+Nf1Wz23u7ed3su68ultwd/je4vuE+6UPVB5UPNR5WPMPi38c6HHuOdHr39vxKPrRvcecxy+eiJ587it+Snta8Uz/Wf1z++fH+wP7u/6Y9kffi9wXwwMlf6r+Wf3S/OWRv1h/dQwmDPa9Er4aeb3yjdab2reOb9uGIocevst+N/y+9IPWh7qPrh/Pf4r/9Gx49mfS501fLL60fA39en8ke2Qkly1kS48CGGxoaioAr2sBoCXCs0MXABQl2d1LKojsvihF4D9h2f1MKs4A1LIAiF0MQBg8o2yFzQRiKuwlR+8YFkAdHMaaXESpDvayWFR4gyF8GBl5owsAqQWAL8KRkeEtIyNfdkGydwBozZPd+SRChOf77RYS1NlBAT/KPwHfOGvYECjNdgAAAAlwSFlzAAAWJQAAFiUBSVIk8AAAQABJREFUeAHt3QucFMd96Pv/zC4IBLKQEEhrCbRgWUAWDMLCwSQEsAQRYFlHlnRykzghvuSYOLl2chMgjhPDOXLiJOTBwSE5JLr5OLGxiY0fshDIIJmHHS8YGQnx8IIcA3rwsCSEhEALaGfqVnVv7c7O9KCd3Zntrq5ffz67s9Nd013/b1XP/Lf6MRmlJ2FCAAEEEEAAAQQQQKBIIFv0nKcIIIAAAggggAACCAQCJIp0BAQQQAABBBBAAIFIARLFSBZmIoAAAggggAACCJAo0gcQQAABBBBAAAEEIgVIFCNZmIkAAggggAACCCBAokgfQAABBBBAAAEEEIgUIFGMZGEmAggggAACCCCAAIkifQABBBBAAAEEEEAgUoBEMZKFmQgggAACCCCAAAIkivQBBBBAAAEEEEAAgUgBEsVIFmYigAACCCCAAAIIkCjSBxBAAAEEEEAAAQQiBUgUI1mYiQACCCCAAAIIIECiSB9AAAEEEEAAAQQQiBQgUYxkYSYCCCCAAAIIIIAAiSJ9AAEEEEAAAQQQQCBSgEQxkoWZCCCAAAIIIIAAAiSK9AEEEEAAAQQQQACBSAESxUgWZiKAAAIIIIAAAgiQKNIHEEAAAQQQQAABBCIFSBQjWZiJAAIIIIAAAgggUA+BfwLfP6lkzY/zsnBsVj5wY8YbgJ+1Ktl2QsmPXxU5pf9uvCojk4ZmZO4IkUwm/Q5H31Cy9biSljMib7yl5GYd/88Pz8gdHvWB4s7e2qbkD5rz0poT+eKsuuLFqXr+o5eV7H9VXTamu0ZkpOHK9O8LT7+iZOPzSl44p6R/XUZGXSVy7yjzmM7YT76p5DsvXL7tCzvG/JEZGT4wnRYmznP6/e/rR/R74Wsir14IPwvefbXI3TdnZGB9euMubONK/iZRrEQrJWUfOpSX750SmTfSvHH4sVM8pj8Ulv4wL69dKmxEE7+SpmtEVk3Lypgh6bX4t8N5+YunlVzQCVHnpOT//FjJhGtFvjAzK9en+IOhM+auf/35U0o2vSDSz4NjK//foTA56irQ9dlYvQ80XNl1XtqeLftRXr5wuDBpCv9efVDJpyZl5GPj0tcZjr0hsuxHhTFfvlXfc61JFC9fxtWlm3XCvER/Fpy5WBhBaPO/9yv5+/dnZer16f0sKIy6u3+TKHZXKgXllFLy18+YUbUUBFNBCDv0COrHvp8PXmFGDz88yiRFIk+fVvJ5/cZwUI+w/fb38vLY3KwM7pe+N4htehTxM+0fEr9+ix5B1aMFuivI5heVPPqcGWUS+V3t87U7s1KXTV/85bqKGV394k+6/+FZbj2uzG85E8a6dGJG+pfJhRr1yFqapxV7wyTx2itE7mnMyJ16NP0lfXThm0eVfF//82z+cZhwrZL3pyxRuEEn/7916+X37XNviXxdOwzQA+vm/TGN00E9ov7//CAf/MM8dbjI/9D/FJiE2Bxle/iYkmdfF/kd/V647e6sXHPF5b3S6FMuJhLFcjIpmf+cPtxoDrEcPy+yRScGp1pTElg3w8jrjOgvngqTxF8ZnZG/1f8t2um26zIy+0Ylv7wpL+Y/7n9/VsnvNaXvzeHB9vj/3wkZ+cP3dMY/850Z+bVblHzwO3nZ/bLIAZ0wTxxqddL9aA43Ld6VD0ZTTaKc9skcYj+q+/iwASKfGN/ZB9Ied2F8Jhn4Bz1qaJLkL83Kynv0aSfhlJH7R+vEcXNOnnpFL9P/PKQtUTSH1D87xcZbqBL+bQYRFu4I3yf/dmpGbhpcvmzpq92Zs/a/wqMqk/T73Lo7slLf/o+xOQXp/x6j5I6N+eCzcp0u97sp/CzoaUv5+Y7RUy0HX2dGy/5ybzhy4luSaJrL/IdozkPRpyHJH+mRlOJphH5D/LA+N8lMz+gRxrRN5tyk/zorwSjB7/xcafwT9CEmc36Wmcx/275M5jSEN/QIijnM5MNk9gPTuuY0C1+nb+jRMjP90XsyBUlip4b5J8qchvGmTqp9m/5un5LHj+vRtHEZPdKa3n3CvsfP00dVbJJo23qQPpr0C+0jyYf1/sLUKZDeHtEZYyr+eqhFj36sz8mcjV1OMusS216d6JgyUx/OycVc+Gb33mH6/LMZ2S4/rn5Y9MTg5Jsh0WidDJU7SX/EoLDMC+e6cCbuSU/iP6T/UTCTOaR4ZZmTtNvCgQR92D0sm+TfPTEojuc/fprXh91F/uS2jJh+4dLU0/hbXgvfD8ZdU/rPgkvxm7r2xOCCfj+0F3OYQ85R04yGjGyaWyf/NjPZFzX1JP6oeO28x/Q5e6sOKH1hmwTnaNr5SX7sqcHN7SOlrW3R0ZmL2szk2vtCWOva/SZRrJ1tVddsrkY0F2KY0TH7X1HxBjbq881MmffrK1mvMENoejIXKNx5U9efofr8HBennhiYc5E+pv9LXjAm+sPBOPxUH5Iz0+h3lC8Tloj3d0/in6XPwXrh1+vk8fnRH347f6bkOZ0gX6HfCVy4+rknBoWtdkyfirFcn6857XqRj77NOVuFr0vK3z2N31zpbibzT+IeffXz3+/LB1d7/90z+txcfWpKLu/OKFpPDJ7Sp1ac18nBLe8QuXFQuJ+fuRjeBcEkkC/qq59dmXoSf7nYzN0PPr07/E9x+XvdOUe5pwazbwolvqXPRzRXPhdO5ujLdn1XDDPN1p+ZTJ0CnKPYaZHov8whUnPy7a6XJLgAYWLH+TWd1d7UfvuD+/S5eGmcemJgnKKsrI+5Zc4m/UFppvdp3yRPPYm/OB5zLtLP9Hmqpy+ImIt8/lGfs2Wu+P2L92XEHHpJ+tQbA5MM/b6+FY6J8u+mZttvidT1wyKt8R9qH1H86k/NRRvFMSsZrxPIv9Em4/WpCEmfetIHXtLnpJrpZj2CbM5PNRevPamTx8Jp3BCRf/iF5N/9oCfxF8ZZ+Le5mO8V/V5gbgtjTkNxZeqpwYd0nOY8VHM++tzH8rJA/7N4gx5M2aoTRDOy+qb+Z+J/vjcjP5eCkfdqtiUjitXUrPG6HmhPAB9tT2wKN2fuj/a8Hhm6QV/BZUZL0jpV0+A1PaJgrvZ9XY/CmpGGX9NXBCd96m385o1wyrfycpd+kzTnrp7V5+n9ib4lyK+8y523gp4amNufmA+J5fqDwOWT9XsSvzkSYabd+h/Nj+rR9X/5paw+xJqVT47X943Tg83mQqbf2KZvH6X3CRemSg1MMmQmM3D6wBP5oB984J36an993u49OnkY0j88WjNf7xcHHDhXt9L4w+i7/jb3Vf1XfZsgc0bKkojzt7uWTt6znhiY8xI/e3tGZjRIcAHj/9qj5OP/mZf1R8wIo4hJJD/y7uR/DvR1a7jz6dDXMgncnrkJqnlTf1FfwWxuGFs42VExc9PYbIpvHl0tA5NYf2hzeLWvSa7NB2e/9ivgCl2T9ndv46/Te/y9+hwt82NO3DfTg08peeDxXMmhmHBp8n73xMCcv7tSj56Y5OBXb3H7ba/S+F+/pIJ7I47VI2brZ2flwduz+ibz4Y3Wl0zMyub5WblaJ0ommfqcvtemC1OlBmYE3Uzm1mCn9HnLX9cO/65vsP4nt2Vl9S9m9akZ2eCw/EV9FNbcZzHpU6XxR8XzV0/n5S0d6n2O3mi8Jwan9Wjyb27P66Mp4QWOU/Q5/Oa90FwFbSZzi5xZG/J60MWN/SCsde1/u/2OWXufRG3BHBo098AzU/GoorkFjpnuT+lh5yA4/au3BuYin7/S91K7W98SxtwuxLxBfHNOVt59tRv/RfY2/gH63NXP68Nr5secuG/unXiVvojFnNLwN/oemy5MlRqYW8N8Ut87zcS5Qh9edX2qNP6r+2dk87zwPFVzS6jiydw6ZbG+EthMT+h7S7owVWpgTq+w0x/o20TdPqyrww3622j+8n1hIXNI+nD7oXr7mqQ9Vhp/cf1NwmQu6DKTq6cq9cTgt3SSuF3/s3Dr1RL8c/DNOXXBe+GGu+rkW/pzYLi+fdQLeiDmU/quCEydAgW7T+dM/kquQMdwu75wxZxvZiZzI12T9JjzjG51JOHpjXBPDcwo7F36non2vDzzLQwP6zcHc76LS1NP44+K0dwvbpk+FGsmc56OK1MlBmaUzOwfJs5r9MjZJf3Pgv0xIyp2svPMvTeTPlUSf3dima6v+DXTy3rkzVzk4cJUicE1BRfwmdHUqMkk0fZCv584cHuUSuIvjvfbeuRM7wbBqUrm3HdXp0oMzI3V954OI/3n6aWDA+afh7/X39Blph/qf5zNP5hMoQCJomM9wZx/aL5i64Q+fPJ0e6e3h53TPppom6onBmbE9cNb8sE9BWfpw4/b9Z33f6/Jnav8bOzmsZL4NzyXl9UH8pf9jt+Z7UmCuem4uUG7C1MlBnvaT9P4w51K3vUf+S4/Y78WZoomYbTLzHfAJn2qJP7uxGISaDuZQ7MuTJUYXKdHiuxkvqWk3HR9+zJzkVvSp0riL47FnJNnJnMRi8vfc1+Jwbb2f4TNrcJuKTOgMv0GCW4Tdkm/H+z6WbGav89JFB1re3P+oTmnxEyP6P8KzWSudjZ3wyl3f7CgUIp+VWpgru79XX3CsvkP+kF9IvMX9blJ9hYZLrJUEv8P9NeSma9tNCMI5abCJe13VSpXNDHzKzG4UX/4m5uKR/0UfmWdXX6VPlSb9KmS+M33fJtvHfmngwXDp0UB/lTflN1MJvJCk2BmQn9VYmBGzm2rmnO8y00vtt9L1YWjDJXEXxjvf72ugouXzLwP6fPzXJ56YnC597hCjRSf6l9xk5MoVkwW/wvscLsZJXtW7/TmWxfMVVzXDSjs5vHXs5Y16K7BW/oyx888mQ+udvycvgXMR8eko8t3N/5b9Lk4ZjL3irM3YQ/ndP42X+1oJnPPSZeuBu6uwUMz6uR7H4r++a6+iMFM5hw2W6bcocmgYIJ+dTd+0672q+nMjaejJvutJeaCl4Flbswe9bq453XXwLw33q4vXDCT+V7nqMl897e5C4AJ317oFVUuSfO6G39hnfe1X9Vt4jSnK7k+ddfA3v7niP6nqNzFKuZcbXP1s5ne036xX/jM79/p+NT0rA3NjaFv0xdhmK/k++yecJTAl8POtqm7a7BBn8tpzk97l779za/fkp5Eurvx21t/mJtqf3q3Kjnv5nGdJP65vurZTP/dsQuhumtg+0zaHrsb/7Qbwtu/mJE0c/jd3GS5cPrKT/LyZf3dtmb608lufSR018DEZm978n9+HN4zz8yzk7nP5J/qfyjN9CvvypT9FidbPimPlcRv63y4/VZJZgS9+GvsbBmXHrtrYC5gMf8ImZ7+O/q2aC8UXdlszvX/o51hHzB3R7jWo4GXt2tvbrj9dkIJXW7+i3pa3/Jju77M31zN6eOd5Ltj8KP2m+qar/J7/7fLH3ozzTzrnZ1XPia02btUqzvxD9M3k/3slIy+6lfJ1/R5SeYwvLnS21wx+GP9xnio/UPjfXq05Y/1xT2uTd0xcC2mSurbnfjNaNoqfZL+An3Fp/nH6T/1Dbdvv06/b+hD7Pv1e8hP2g87L9LfYGS+xs61qTsGJqYPj8rK0bN5+d/66+o+pm+4bb6lZuyQjBw/r/TtxkTMrXHMKNJix+4p2N34bbuao1Bmenf70QY73+XH7hiYpHiNvojF3Ctz/6siM/VtcMyXLNyor3h/TieN5mp3e4HPSk++A767be7Wv4/djcqDcuYk5P7trfdBfcscc9sT36buGNivOzQ3mj6uR1Qu92NuGeHS1J34TTz/rTErG+dmxSSDL+lRaHNbDHP4zSSJ5h6S5ga06+7IOjm60F0Dl9q1krp2N/4P6K9y3HhXVn5BXwx35qK+NcjxsA8c0aPt5htJ1n4gK3/m2GiidequgSn/R/q+kZ+ZnAn2BXPKjjnkbg43XqsvdjE3Ije3ynLtFJ5K4jcGJm4zpekOGd01eJc+Grf1g1n5v/SosT4rSf/TJPJV/Q+06QPm9BPzda9P6OWMJoZ9xP7O6FusuPXpaGvOIwIIVCxgzlEzVzebxPnmwSJDObxSsaHrLzC3/TAXr5h/Lc05rPZ74V2Pq9L6Gwfzz9JI9oNK6VJRvk1nimbgwJzC9U59wduNgyTVX1bRm0YjUeyNHq9FAAEEEEAAAQRSLMCh5xQ3LqEhgAACCCCAAAK9ESBR7I0er0UAAQQQQAABBFIsQKKY4sYlNAQQQAABBBBAoDcCJIq90eO1CCCAAAIIIIBAigVIFFPcuISGAAIIIIAAAgj0RoBEsTd6vBYBBBBAAAEEEEixAIliihuX0BBAAAEEEEAAgd4IkCj2Ro/XIoAAAggggAACKRYgUUxx4xIaAggggAACCCDQGwESxd7o8VoEEEAAAQQQQCDFAiSKKW5cQkMAAQQQQAABBHojQKLYGz1eiwACCCCAAAIIpFiARDHFjUtoCCCAAAIIIIBAbwRIFHujx2sRQAABBBBAAIEUC5AoprhxCQ0BBBBAAAEEEOiNAIlib/R4LQIIIIAAAgggkGIBEsUUNy6hIYAAAggggAACvREgUeyNHq9FAAEEEEAAAQRSLECimOLGJTQEEEAAAQQQQKA3AiSKvdHjtQgggAACCCCAQIoF6lMcWyJCy2QyfVoPpVSfbo+NIYAAAggg4KIAn8/dazVGFLvnRCkEEEAAAQQQQMA7ARJF75qcgBFAAAEEEEAAge4JkCh2z4lSCCCAAAIIIICAdwIkit41OQEjgAACCCCAAALdE+Bilu45VbUUF5xUlZOVIYAAAgggULFALT+L+/pCmYqDr+AFjChWgEVRBBBAAAEEEEDAJwESRZ9am1gRQAABBBBAAIEKBEgUK8CiKAIIIIAAAggg4JMAiaJPrU2sCCCAAAIIIIBABQIkihVgURQBBBBAAAEEEPBJgETRp9YmVgQQQAABBBBAoAIBEsUKsCiKAAIIIIAAAgj4JECi6FNrEysCCCCAAAIIIFCBAIliBVgURQABBBBAAAEEfBLw8ptZvn9SyZof52Xh2Kx84MZMqtq7ublZtm/fLgcOHJB+/fpJU1OTzJkzRyZNmpSqOLsbzIIFC+TSpUuybt267r4kVeV8jd/3/cD3+M1O7LuB7/HTB6r4Uaa/wsa76Te2tqmb1raptc/mah67bipV/FOLjba2tqqFCxeWbMtsu66uTi1evFjlcrWPtxax9XSdu3fvDjwaGhp6ugqnX+dj/L7vB77Hb3ZY3w18jz8pfaD4c988d3Vyt+Y9EM/n8+ovn84FSWLaEsWlS5cGSVE2m1VLlixRW7duVZs3b1aLFi3qSB5XrlzZAzU3X9LS0qIaGxu9TRR9jd/3/cD3+M27le8GvseflD5AouhQ7nDsbF7944Gc+vQPc+r2b4QjiSZJTFOieOzYsWDU0HTMNWvWlLTO8uXLg4Rp0KBB6uzZsyXL0zJj7dq1atmyZWr27Nmqvr6+I0H2ZUTR9/h93w98j9+8j/lu4Hv8SeoDJIoOZRYbn8t3jCDaBNE+puXQ86pVq4KkaNSoUaqtra2kdc6dO6eGDBkSlFm/fn3J8rTMGD9+fEdyWLiT+pIo+h6/7/uB7/Gb9zHfDXyPP0l9oPAzyP7t6metM1c9P9SSlwnrczJnY06bR097T6ugzNSHc3IxZ3IGkfcOE/nCjGyXn6Zrol/v6twdO3YEVdcjaaLPRywJQ48kyvTp04P55kKXtE6rV6+WDRs2dPysWLEiraFGxuV7/L7vB77Hb3YK3w18j58+EPnR0OuZzlz1fNeIjDz4lJLXLok8oxPCiUNLr1be+Fy4/E59JfMVdeHy6wdm5Pqbujp94XDX564/O3r0aBDChAkTyoaiR5uCBEofmihbxvUFM2bM6BLC0KFDuzxP+xPf4/d9P/A9frN/+27ge/z0gdp8yjkzojhicEamDg8RHtUJYdS06YVw/n2jS5PIqPJpmXfq1KkglGHD9PBpmWn48BDv5MmTZUowGwG3BXzfD3yP3/Re3w18j58+UJv3cGcSRRP+A+0J4KPPlyaK+19V8vw5kRsGiky7vjZYSV3rhQsXgqoNHKiDLzMNGDAgWHLx4sUyJZiNgNsCvu8Hvsdveq/vBr7HTx+ozXu4U4ni/JEZGahPwXvxvMjTr3RNFje1J4/3jspINuPXiKK+P2K3e0clZbu9UgoikACBSvp2JWUTEFq3qlBJTJWU7dbGE1KokrgqKZuQ8N62GpXEVEnZt91wggpUElclZRMUYp9XxalEcVC/jMzVyaKZikcVN7Ynivd7dtjZWPTv3988yOVGC+0y820tTAikUcD3/cD3+E2f9t3A9/jpA7V5Z3cqUTQEHYef9XmK+lLzQKXljJKjb4iM11cz33q1X6OJBmDw4MGBg74NTvAY9ev8eT0MqydbNqoM8xBwWcD2bV/3A9/jN33XdwPf46cP1OYd3LlE0Zx/2HClyIk39eHn0yGKPezs42iiERg5cmQAcfhw+cu57TJbNpTjNwLpEbB92/b1qMjsMls2qoyr82xMNsaoOOwyWzaqjMvzbFw2zqhY7DJbNqqMq/NsTDbGqDjsMls2qozL82xcNs6oWOwyWzaqDPM6BZxLFM35h/fp8xDN9MixcETRXO1s7oZzT6N/o4nGYezYseZB9u/fHzxG/dq3b18we9y4cVGLmYeA8wK+7we+x286sO8GvsdPH6jN27hziaJhsIefzXmJz75ufkRmNIhcN8DPRHH+/PlB79iyZYscPHiwpKds27ZN9u7dG8yfN29eyXJmIJAGAd/3A9/jN33YdwPf46cP1Oid3NWvlLn7sfD7mj/y3fDxkWO5bofya0+k67ueW1tbVWNjoxleVfobWNTx48c7LI4cOaKampqCZZMnT1b5fL5jWdr/aG5uDuL25Sv8itvTt/h93w98j9/0f98NfI8/SX3AfB4X/xS/R7vy3FwQ4uT0xcO5ju9wHvfVNtXa1v0EKG2JomnAxx9/XNXX1wcdM5vNqjvuuENNmzato6Pq+ygqParoZFv3tNK+JUrFTj7G7/t+4Hv8Zh/w3cD3+JPSB4qTRPPc1cnZmp+5kFejvxKODC7Z2f3RRNNQaUwUTVx79uxRU6ZMUZlMpiNBNEnjzJkzlT551xTxavIxUSpsYF/j930/8D1+sw/4buB7/EnoA2lKFDMGVAfEVCMBnbSVrLnW5OZWOIcOHRI9wihjxowR+60sJRVhBgIpFvB9P/A9ftO1fTfwPf44+0Acn/21ejsnUayVbPt609RZakzF6hFAAAEEEEiFQJo++5286jkVvYggEEAAAQQQQACBhAuQKCa8gageAggggAACCCAQlwCJYlzybBcBBBBAAAEEEEi4AIliwhuI6iGAAAIIIIAAAnEJkCjGJc92EUAAAQQQQACBhAuQKCa8gageAggggAACCCAQlwCJYlzybBcBBBBAAAEEEEi4AIliwhuI6iGAAAIIIIAAAnEJkCjGJc92EUAAAQQQQACBhAuQKCa8gageAggggAACCCAQlwCJYlzybBcBBBBAAAEEEEi4AIliwhuI6iGAAAIIIIAAAnEJkCjGJc92EUAAAQQQQACBhAuQKCa8gageAggggAACCCAQlwCJYlzybBcBBBBAAAEEEEi4AIliwhuI6iGAAAIIIIAAAnEJkCjGJc92EUAAAQQQQACBhAuQKCa8gageAggggAACCCAQlwCJYlzybBcBBBBAAAEEEEi4AIliwhuI6iGAAAIIIIAAAnEJkCjGJc92EUAAAQQQQACBhAuQKCa8gageAggggAACCCAQlwCJYlzybBcBBBBAAAEEEEi4AIliwhuI6iGAAAIIIIAAAnEJkCjGJc92EUAAAQQQQACBhAuQKCa8gageAggggAACCCAQlwCJYlzybBcBBBBAAAEEEEi4AIliwhuI6iGAAAIIIIAAAnEJkCjGJc92EUAAAQQQQACBhAuQKCa8gageAggggAACCCAQlwCJYlzybBcBBBBAAAEEEEi4AIliwhuI6iGAAAIIIIAAAnEJkCjGJc92EUAAAQQQQACBhAuQKCa8gageAggggAACCCAQlwCJYlzybBcBBBBAAAEEEEi4QH3C61e16v2sVcm2E0p+/KrIKf1341UZmTQ0I3NHiGQymaptJ0krWrBggVy6dEnWrVuXpGrVvC7Nzc2yfft2OXDggPTr10+amppkzpw5MmnSpJpvOwkb8D3+4jbwdT+wDr7G7/t+4Hv8pv9jYN8FevmoPJg2PZdX47/Wpm5aW/rzyxvb1KEz+Zop6OZRxT8121jBinfv3h1st6GhoWBuuv9sbW1VCxcuLPE2/nV1dWrx4sUql8ulFsH3+KMa1sf9oNDBx/h93w98j9/0/yQYFH/um+euTu7WvJvi20/kOxLE/7GjTT32fF499XJe/euhnJq4Pkwcf/HbbeqNS7VJFuPoLC0tLaqxsdG7RHHp0qVBzNlsVi1ZskRt3bpVbd68WS1atKgjeVy5cmU3e457xXyPv7jFfN0PrIOv8fu+H/gev+n/STCI47Pf7vvVfkx1opjL59XsR8Nk8I+aS0eSnn8jr8Z9NVy++kDp8mpg91VnWbt2rVq2bJmaPXu2qq+v70iMfBlRPHbsWDBqaLzXrFlT0nTLly8PTAYNGqTOnj1bstz1Gb7Hb9vP9/3A9/h93w98j9+8DyTFoK8+++17Xy0fU50otuhDyuZw881fblMnzkePGP7p7lxQxow21mLqq84yfvz4juSwcJu+JIqrVq0K4h81apRqaytty3PnzqkhQ4YEZdavX1+Lpo51nb7Hb/F93w98j9/3/cD3+M37QFIMCj+H7d/2fcq1R2euen6oJS8T1udkzsacNo+e9p5WQZmpD+fkYk7JyTfDcqOvEmm4MvqClRGDwjIvnItepytzV69eLRs2bOj4WbFihStVr0o9d+zYEaxHj6iKPh+xZJ16JFGmT58ezDcXuqRt8j1+256+7we+x+/7fuB7/OZ9AAP7bli9R2euer5rREYefErJa5dEntEJ4UR9xXLxtPG5cPmdN2bkirqMXHuFko+Ny8jIwcUlO5//9I3w79HvKF1fZ6nk/zVjxowulRw6dGiX52l/cvTo0SDECRMmlA1Vj7YEibQ+NFG2jKsLfI/ftpvv+4Hv8fu+H/gev3kfwMC+G1bv0ZlEccTgjEwdLrLrJZFHdUIYlShuesEcWRS5b3SY9JkyUeUsn7llzqbnw9e8T6+byV2BU6dOBZUfNmxY2SCGDw8b+eTJk2XLuLrA9/hdbTfqXV0B3/cD3+M3vQmD6u5TZm3OHHo2lX2gPQF8tD25M/PstP9VJc/rw8c3DBSZdr2dW/7xtYtKfvf7eXldj1De8g6RX7vF7RHF8pH6seTChQtBoAMH6g5QZhowYECw5OLFi2VKuDvb9/jdbTlqXk0B3/cD3+M3fQmDau5R4bqcShTnj8zIQH362YvnRZ5+JRwJtCR2ZPDeURnJvs0NtE1S+aHNedn9cphY/ssvZaVflkTRWrr4qO+P2O1qV1K22yuNuWAlMVVSNuaw2DwCFQlU0rcrKVtRJWIsXElMlZSNMaSKN11JXJWUrbgiKXqBU4nioH76m1R0smim4lHFje2jjPe3jzpGtZG5wOWv9ubl7u/k5ag+N3GSPo3vm3Oy8u6rSRKjvFya179//6C6lxsttMvMt7WkbfI9/rS1J/H0TMD3/cD3+E2vwaBn+87lXuVUomgC6Tj8rM9T1JeYB7G1nFFB4jf+GpFbyyR9ZgTyrk15+ceDSo8einxqUkYe1kmiOfeRyX2BwYPDK5b0bXDKBnP+vB6K1pMtW7aggwtsTL7G72CTUeUaCPi+H/gev+lSGFR/x3IuUTTnHzZcKXJC3/rm6dMhiD3sXG400Yw2fnhLXv7rrMisd4psvzsrv9eUlToON1e/R8W0xpEjRwZbPnz4cNka2GW2bNmCDi6wMdkYo0Kwy2zZqDLMQ8BlAdu3bV+PisUus2Wjyrg6z8ZkY4yKwy6zZaPKuDzPxmXjjIrFLrNlo8owr1PAuUTRnH94nz4P0UyPHAtHFM3VzvpuOHJPY+no4I6T+qKV/8yLPuosD96ekS/OqpMbB5WW6yThLxcFxo4dG1R7//79Zau/b9++YNm4cePKlnF1ge/xu9pu1Lu6Ar7vB77Hb3oTBtXdp8zanEsUTaXt4WczUvjs6+ZHZEaDyHUDuiaAb+WVfObJvOgH+dz7MvLRMU6Ga0JmehuB+fPnByW2bNkiBw8eLCm9bds22bt3bzB/3rx5Jctdn+F7/K63H/WvjoDv+4Hv8ZtehEF19qXCtTiZOZmbY9+mL0Q51Sry2T35IJ6ow84b9HmM5qKVd+nb3/w6t78pbPfU/T1nzhxpbGwU/fV98vGPf1xOnDjREaO5AesnPvGJ4PnkyZPl9ttv71iWlj98jz8t7UgcvRPwfT/wPX7TezDo3T4U9eqM+c7BqAVJn/elZ/Py6SfDql+lL2J96r6sDDDHnwumT+/Oy5d+ouRKfVvxa64oWBDx56x3ZuQv31f9vDmjD5UXT31BvnPnTpk2bZro73rukjQV1yVNz5944gmZO3dukCxms1mZNWuWtLa2SnNzcxCmuY/irl27ZOLEiWkKuyMW3+PvgCj4w8f9oCB88TF+3/cD3+M3/T8JBnF99hfu/9X6u/qZUbVq9jbrufvmjPRvr/0H9S1zipNE83LzVX9merNN5Li+4PVyP6cvOJkvB/HxKxS488475Yc//KFMmTIluCL+u9/9bpAkmqRx5syZ8swzz6Q2STQCvsfPfoAA+wHvA/SB6r8PODuiWH2K2qwxTf9V1EaoNms1t8I5dOiQ1NfXy5gxY8R+K0tttpa8tfoef/JahBrFIeD7fuB7/KbPxWWQps9+EsUav3ulqbPUmIrVI4AAAgggkAqBNH32O3voORU9iSAQQAABBBBAAIEEC5AoJrhxqBoCCCCAAAIIIBCnAIlinPpsGwEEEEAAAQQQSLAAiWKCG4eqIYAAAggggAACcQqQKMapz7YRQAABBBBAAIEEC5AoJrhxqBoCCCCAAAIIIBCnAIlinPpsGwEEEEAAAQQQSLAAiWKCG4eqIYAAAggggAACcQqQKMapz7YRQAABBBBAAIEEC5AoJrhxqBoCCCCAAAIIIBCnAIlinPpsGwEEEEAAAQQQSLAAiWKCG4eqIYAAAggggAACcQqQKMapz7YRQAABBBBAAIEEC5AoJrhxqBoCCCCAAAIIIBCnAIlinPpsGwEEEEAAAQQQSLAAiWKCG4eqIYAAAggggAACcQqQKMapz7YRQAABBBBAAIEEC5AoJrhxqBoCCCCAAAIIIBCnAIlinPpsGwEEEEAAAQQQSLAAiWKCG4eqIYAAAggggAACcQqQKMapz7YRQAABBBBAAIEEC5AoJrhxqBoCCCCAAAIIIBCnAIlinPpsGwEEEEAAAQQQSLAAiWKCG4eqIYAAAggggAACcQqQKMapz7YRQAABBBBAAIEEC5AoJrhxqBoCCCCAAAIIIBCnAIlinPpsGwEEEEAAAQQQSLAAiWKCG4eqIYAAAggggAACcQqQKMapz7YRQAABBBBAAIEEC5AoJrhxqBoCCCCAAAIIIBCnAIlinPpsGwEEEEAAAQQQSLAAiWKCG4eqIYAAAggggAACcQqQKMapz7YRQAABBBBAAIEEC5AoJrhxqBoCCCCAAAIIIBCnAIlinPpsGwEEEEAAAQQQSLBAfYLrVtWqHX1DydbjSlrOiLzxlpKbr8rIzw/PyB03Zqq6nSStbMGCBXLp0iVZt25dkqpV87o0NzfL9u3b5cCBA9KvXz9pamqSOXPmyKRJk2q+7SRswPf4TRv4buB7/MX7oa/vhdbB1/jZD2wP6OWj8mD6wqGcumVdm7ppbenP3E1t6tSb+Zop6OZRxT8121jBinfv3h1st6GhoWBuuv9sbW1VCxcuLPE2/nV1dWrx4sUql8ulFsH3+E3D+m7ge/xRO7eP74WFDj7Gn4T9oPhz3zx3dXK35t0U3/piviNB/ONdObX9RF5tO55Xn/phTo3/Wpg4fnhzm2rL1SZZjKOztLS0qMbGRu8SxaVLlwYxZ7NZtWTJErV161a1efNmtWjRoo7kceXKld3sOe4V8z1+02K+G/gef/Fe6+t7oXXwNf4k7AdxfPbbdq/2Y+oTxZmPhMng3z1TOpK073RejfxyuHzvK24nimvXrlXLli1Ts2fPVvX19R2JkS8jiseOHQtGDc3OuWbNmpL9ZPny5YHJoEGD1NmzZ0uWuz7D9/hN+/lu4Hv8dh/2/b3Q9/iTsh+QKNo9MuGPJ86Ho4nmsPP5t6ITwRntieSXny1NJKsRXl91lvHjx3ckh4Xb9CVRXLVqVRD/qFGjVFtbW0nTnTt3Tg0ZMiQos379+pLlrs/wPX7Tfr4b+B6/3Yd9fy/0Pf6k7AeFn8P2b9tHXXt05qrnh1ryMmF9TuZszGnz6GnvaRWUmfpwTi7mlBzSF66YqfEqkSvroy9aacuHZQb3Cx9d/b169WrZsGFDx8+KFStcDaVH9d6xY0fwOj2iKvp8xJJ16JFEmT59ejDfXOiStsn3+E17+m7ge/x2n/b9vdD3+NkP7J5QvUdnrnq+a0RGHnxKyWuXRJ7RCeHEoaWJ38bnwuV36iuZr6jLyKwbRV749dKkwfLt/JmS586JXKHTZdevfp4xY4YNK3gcOnRol+dpf3L06NEgxAkTJpQNVf+nHSTS+tBE2TKuLvA9ftNuvhv4Hr/dd31/L/Q9fvYDuydU79GZEcURgzMydXgY+KM6IYyaNr0Qzr9vdGkSacrr4V459aaSg68q+aeDefntHXnppwX+4n0ZGdQv+jVR22Fe8gROnToVVGrYsGFlKzd8eNiBTp48WbaMqwt8j9+0m+8Gvsfv6r5LvasrwH5QXU+zNmdGFE1lH9AJ4K6XlDz6vJI/nWzmdE77dfL3vB4dvGGgyLTrO+cX/vVmm8iUb7Ufa25fsGxyRn7lXc7ky4Xh8HeBwIULF4JnAwfqDlBmGjBgQLDk4sWLZUq4O9v3+E3L+W7ge/zu7r3UvJoC7AfV1AzX5VSGNH9kRgbqI8kvnhd5+pWuo4qbdPJopntHZSSbiR4drNPR3tuYCX4mXBsCmMPZDzyek3P6JtxM7gro+yN2u/KVlO32SmMuWElMlZSNOayKNl9JXJWUragSMRauJKZKysYYEptGoGKBSvp2JWUrrkiKXuBUomgOD8/VyaKZzKhi4bSx/fn9ZQ47m7ID9HmLn/+FbPCzaW6dfO3OrFylL2LZ9ZLI3zzTdX2F6+bv5Av0798/qOTlRgvtMvNtLWmbfI/ftKfvBr7Hn7Z9mnh6JsB+0DO3y73KqUTRBGIOP5vJnKdozjk0U8sZJUffEBl/jcitV0ePJgYFi369//qMLHtvWH7rCRLFIh6nng4ePDior74NTtl6nz+vh6L1ZMuWLejgAhuTr/EXtquvBvQBB3dcqlx1AfaDqpOKc4miOf+w4UqRE2/qw8+nQxB72Ll4NHHDc3lZfSAv5vzFctPMhjBRPKYTzef090EzuSkwcuTIoOKHDx8uG4BdZsuWLejgAhuTjTEqBLvMlo0q4/I8G5eNMyoWu8yWjSrj6jwbk40xKg67zJaNKsM8BFwWsH3b9vWoWOwyWzaqDPM6BZxLFM35h/fp8xDN9MixMLEzVzvro8pyjz7/sHD6gb4Q9q/1IeVvt5crXGb/LkwNzTqY3BQYO3ZsUPH9+/eXDWDfvn3BsnHjxpUt4+oC3+M37ea7ge/xu7rvUu/qCrAfVNfTrM25RNFU2h5+NuclPvu6+RGZ0SBy3YCumd4tV5vSIt/RiaS5AXfUtOXFcP61V4jcpG/Bw+SmwPz584OKb9myRQ4ePFgSxLZt22Tv3r3B/Hnz5pUsd32G7/Gb9vPdwPf4Xd+HqX91BNgPquNYuBYnE8XR78jIbfp+0qdaRT67J7zdTfFhZxPkPTdnZIi+xsHcVPvTu5W0tnVNFh/XSeKf66uezfTfL3MRTFCAX4kWmDNnjjQ2Nor++j75+Mc/LidOnOior7kB6yc+8Yng+eTJk+X222/vWJaWP3yP37Sj7wa+x5+WfZk4eifAftA7v6hXZ8x3DkYtSPq8Lz2bl08/GVbdXLn81H3Z4Krm4no/fCwvn/yBvvBFL7he32Jvkk4wzdXTP9YXwBx6LSz9Pn2P5q/qK6Drs9UfUczoQ+XFU1+Q79y5U6ZNmyb6u567JE3FdUnT8yeeeELmzp0bJIvZbFZmzZolra2t0tzcHIRp7qO4a9cumThxYprC7ojF9/gNhO8GvsffsTMU/OHje2FB+OJj/EnYD+L67C9s+6r9bRJFF6czF/Jq9Ffa1E1r29SSnbnLhrDvdF59eHObGqHLmvL25/ZvtKkvHMqpi235y76+Nwt1Q5kctctPb9bX3dfq5CjYpk4Uu/uSVJTbs2ePmjJlitI7aYe5ThrVzJkzlT6BORUxXi4I3+M3Nr4b+B5/8f7h63uhdfA1/rj3g+LPffPc1cnZEUWNXvF0QZ+naK5uNt/QcrO+m8rQonMaK15hN16Qqv8quhFvUoqYW+EcOnRI6uvrZcyYMWK/lSUp9at1PXyP3/j6buB7/LXex1i/GwJx7Qdp+uz3KlGMo1unqbPE4cc2EUAAAQQQcE0gTZ/9Tl7M4lqHob4IIIAAAggggICLAiSKLrYadUYAAQQQQAABBPpAgESxD5DZBAIIIIAAAggg4KIAiaKLrUadEUAAAQQQQACBPhAgUewDZDaBAAIIIIAAAgi4KECi6GKrUWcEEEAAAQQQQKAPBEgU+wCZTSCAAAIIIIAAAi4KkCi62GrUGQEEEEAAAQQQ6AMBEsU+QGYTCCCAAAIIIICAiwIkii62GnVGAAEEEEAAAQT6QIBEsQ+Q2QQCCCCAAAIIIOCiAImii61GnRFAAAEEEEAAgT4QIFHsA2Q2gQACCCCAAAIIuChAouhiq1FnBBBAAAEEEECgDwRIFPsAmU0ggAACCCCAAAIuCpAouthq1BkBBBBAAAEEEOgDARLFPkBmEwgggAACCCCAgIsCJIouthp1RgABBBBAAAEE+kCARLEPkNkEAggggAACCCDgogCJooutRp0RQAABBBBAAIE+ECBR7ANkNoEAAggggAACCLgoQKLoYqtRZwQQQAABBBBAoA8ESBT7AJlNIIAAAggggAACLgqQKLrYatQZAQQQQAABBBDoAwESxT5AZhMIIIAAAggggICLAiSKLrYadUYAAQQQQAABBPpAgESxD5DZBAIIIIAAAggg4KIAiaKLrUadEUAAAQQQQACBPhAgUewDZDaBAAIIIIAAAgi4KECi6GKrUWcEEEAAAQQQQKAPBEgU+wCZTSCAAAIIIIAAAi4KkCi62GrUGQEEEEAAAQQQ6AMBEsU+QGYTCCCAAAIIIICAiwIkii62GnVGAAEEEEAAAQT6QIBEsQ+Q2QQCCCCAAAIIIOCiQL2Lla5GnVvblPxBc15acyJfnFVXjVUmYh3Nzc2yfft2OXDggPTr10+amppkzpw5MmnSpETUr68rsWDBArl06ZKsW7eurzcd2/boAyK+G/gev9n5fDfwPf7iN2AfPwuKDXr8XHk6ffqHOXXT2jY16ittNRXQDaOKf2qxwdbWVrVw4cKSbZlt19XVqcWLF6tcLleLTSd2nbt37w48GhoaElvHalaMPqCU7wa+x2/2J98NfI8/6j01js+C4s9989zVyd2a90L8uy/mgyQxTYni0qVLg6Qom82qJUuWqK1bt6rNmzerRYsWdSSPK1eu7IWaWy9taWlRjY2NXiWK9AGlfDfwPX7zLuW7ge/xF39SxfVZQKJY3BIOPT/dmle3fb1Nzd3UlpoRxWPHjgWjhqZjrlmzpqQ1li9fHiRMgwYNUmfPni1ZnpYZa9euVcuWLVOzZ89W9fX1HQmyDyOK9AGlfDfwPX7zPua7ge/x28+yJHwWkCja1nDwceH2NnXLujbVciYcVUzDoedVq1YFSdGoUaNUW1vpofRz586pIUOGBGXWr1/vYKt1r8rjx4/vSA4Ld1IfEkX6gFK+G/gev3mX8N3A9/jtJ0USPgsKP4Ps37Z+rj06c9XzQy15mbA+J3M26qtPykx7T6ugzNSHc3IxZ3KGrtN//DQvm18U+ZPbMjL6qq7LXH62Y8eOoPp6JE30+YgloeiRRJk+fXow31zoktZp9erVsmHDho6fFStWpDXUkrjoAyK+G/gev9kpfDfwPX77xujzZ4E1qOajM1c93zUiIw8+peS1SyLP6IRw4tBMicPG58Lld96YkSvqui4/9oaS5T9SMu16kY/empG38iUvd3bG0aNHg7pPmDChbAz6P6wggdKHJsqWcX3BjBkzuoQwdOjQLs/T/IQ+IOK7ge/xm/3bdwPf47fv8T5/FliDaj46M6I4YnBGpg4PQ39UJ4RR06YXwvn3je6aJObySn5f3wrHzP27qVnJZLouj1qXS/NOnToVVHfYsGFlqz18eIh38uTJsmVY4K4AfUDEdwPf4zd7r+8Gvsfv7jt4smvuTKJoGB9oTwAffb40Udz/qpLnz4ncMFCCUcNC9tUHlTz1isjy92bkJp1wpm26cOFCENLAgTr4MtOAAQOCJRcvXixTgtkuC9AHRHw38D1+s//6buB7/C6/hye57k4livNHZmSgPgXvxfMiT7/SNVnc1J483jsqI9mCEUNz3uLK/Uo+8E6RX73FqXC73W/0/RFrUrbbK6Vg7AL0ARHfDXyP3+yEvhv4Hn/sb8QprYBTmdOgfhmZq5NFMxWPKm5sTxTvLzjsbL595ZM/yMtV/URW6EPOaZ369+8fhHa50UK7zHxbC1P6BOgDIr4b+B6/2at9N/A9/vS9sycjIueyp47Dz/o8RX2JeaDYckbJ0TdExl8jcuvVnYeWP/d0OH+ZPuR8jc6lLukroe1P4cUsdl6+fX3JaJru12Lw4MFBYX0bnLIvOn9eD8PqyZYtW5AFTgrYdvW5D/hu4Hv8Zsf13cD3+J1883ag0s4liuaq5YYrRU68qQ8/nw6F7WHnwtFEs2RP++HpP9yp5F3/ke/yM/Zr4WXPJmG0y75+pOvhbAfaL6jiyJEjg8fDhw+XrbJdZsuWLcgCJwVsu9p2jgrCLrNlo8q4PM/GZeOMisUus2Wjyrg6z8ZkY4yKwy6zZaPKuDzPxmXjjIrFLrNlo8q4Os/GZGOMisMus2WjyjAPgUIB5xJFc/7hffo8RDM9cixM7MzVzuZuOPc0do4mmuU36oRylL5fYtRPY8F9FO3yq/p3fb1ZhwvT2LFjg2ru37+/bHX37dsXLBs3blzZMixwV4A+IOK7ge/xm73XdwPf43f3HTzhNXftDuGmvj99PfxWldu/0aYOvxb+/ZtbS7+R5HKxXWxLzzezfPvb3zYZc/C1dQcOHCgJ23zvs1lufsyXo/syNTc3BzH78M0s9AGlfDfwPX7zvua7ge/xl/tsi+OzwH7mFj6Wq1/S55vz/Jyc7n4s/K7mj3w3fHzkWK6iONKUKLa2tqrGxsYgKdLfwKKOHz/eYXHkyBHV1NQULJs8ebLK5/WZmJ5Mcbw5xEVLH1DKdwPf4zf7nu8Gvsdf7v03js+CwgTR/l2ufkmf72yi+MXDOXXT2jBJHPfVNtWqRwgrmdKUKJq4H3/88WBE0XTIbDar7rjjDjVt2rQgQTTz9H0U1d69eyshcr5sHG8OcaLRB9gP6AP0AfpA6btwHJ8FNjksfCytmRtznE0Uz1zIq9FfCRPFJTsrG000TZO2RNHEtGfPHjVlyhSlv3mmI0E0SePMmTOVPoHZFPFqiuPNIW5g+gD7AX2APkAf6PpOHMdnQWGCaP/uWit3nmVMVXUQTDUSiPq6wFqTm1vhHDp0SOrr62XMmDFiv5WlRiGy2gQK0AdEfDfwPX6zW/pu4Hv8cb41x/HZX6t4SRRrJdu+3jR1lhpTsXoEEEAAAQRSIZCmz37nbo+Tih5EEAgggAACCCCAgAMCJIoONBJVRAABBBBAAAEE4hAgUYxDnW0igAACCCCAAAIOCJAoOtBIVBEBBBBAAAEEEIhDgEQxDnW2iQACCCCAAAIIOCBAouhAI1FFBBBAAAEEEEAgDgESxTjU2SYCCCCAAAIIIOCAAImiA41EFRFAAAEEEEAAgTgESBTjUGebCCCAAAIIIICAAwIkig40ElVEAAEEEEAAAQTiECBRjEOdbSKAAAIIIIAAAg4IkCg60EhUEQEEEEAAAQQQiEOARDEOdbaJAAIIIIAAAgg4IECi6EAjUUUEEEAAAQQQQCAOARLFONTZJgIIIIAAAggg4IAAiaIDjUQVEUAAAQQQQACBOARIFONQZ5sIIIAAAggggIADAiSKDjQSVUQAAQQQQAABBOIQIFGMQ51tIoAAAggggAACDgiQKDrQSFQRAQQQQAABBBCIQ4BEMQ51tokAAggggAACCDggQKLoQCNRRQQQQAABBBBAIA4BEsU41NkmAggggAACCCDggACJogONRBURQAABBBBAAIE4BEgU41BnmwgggAACCCCAgAMCJIoONBJVRAABBBBAAAEE4hAgUYxDnW0igAACCCCAAAIOCJAoOtBIVBEBBBBAAAEEEIhDgEQxDnW2iQACCCCAAAIIOCBAouhAI1FFBBBAAAEEEEAgDgESxTjU2SYCCCCAAAIIIOCAAImiA41EFRFAAAEEEEAAgTgESBTjUGebCCCAAAIIIICAAwIkig40ElVEAAEEEEAAAQTiEKiPY6N9vc0fvaxk/6vqspu9a0RGGq7MXLaMCwubm5tl+/btcuDAAenXr580NTXJnDlzZNKkSS5Uv+p1XLBggVy6dEnWrVtX9XUndYX0ARHfDXyP3+ybvhv4Hn/x+7OPnwXFBj1+rjyYFn0vp25a23bZn+ZT+ZpI6IYxGWqXn1psqLW1VS1cuLDLdux26+rq1OLFi1Uul6vFphO7zt27dwceDQ0Nia1jNStGH1DKdwPf4zf7k+8Gvscf9Z4ax2eB/fwtfIyqmwvzxIVK9raOv/TtMEn8/P6cWnMw+ufEebcTxaVLlwZJUTabVUuWLFFbt25VmzdvVosWLepIHleuXNlbSmde39LSohobG71KFOkDSvlu4Hv85g3KdwPf4y/+kIrrs6AwQbR/F9fNleepTxTffCuvRujRxNu+3hZLm9gOUvhY7YocO3ZMmVFDs401a9aUrH758uXBskGDBqmzZ8+WLE/LjLVr16ply5ap2bNnq/r6+o4E2YcRRfqAUr4b+B6/eR/z3cD3+O1nWRI+Cwo/8+3ftn6uPaY+Udz7Sj445PyR76Y3UVy1alWQFI0aNUq1tZXGee7cOTVkyJCgzPr1613ro92u7/jx4zuSQ7tjmkcfEkX6gFK+G/gev3mj8N3A9/jth0USPgsKP4Ps37Z+rj06c9XzQy15mbA+J3M25rR59LT3tArKTH04JxdzJmcQaXktfBx3jfsXqkRHLbJjx45gkR5JEz2yWFJMjyTK9OnTg/nmQpe0TqtXr5YNGzZ0/KxYsSKtoZbERR9gP6AP0AfoA+Fbo8+fBSUfDlWY4cxVz+aq5AefUvLaJZFndEI4cWhp4rfxuXD5nTdm5Iq6cHnLmVCp6RqRPfrq5x0nlTx/TmTEIJGf08njnJtE6rKl66qCbZ+t4ujRo8G2JkyYUHab+j+sIIHShybKlnF9wYwZM7qEMHTo0C7P0/yEPiDiu4Hv8Zv923cD3+O37/E+fxZYg2o+OpMojhickanDRXa9JPKoTgijEsVNL4Sjh/eN7kz8DrWPKH71p0q+fypc3gmoZLxOIP9malbGX9v5ms7lbvx16tSpoKLDhg0rW+HhwzWenk6ePFm2DAvcFaAPiPhu4Hv8Zu/13cD3+N19B092zZ059GwYH2hPAB99vv5xBC8AACjQSURBVDjhk+A+iWak8IaBItOu70RveS38e7dOMD86JiP/8ktZ+beZWfnk+IwM1EdpD+gRx9/YlpfXLpaus3Mtyf7rwoULQQUHDtTBl5kGDBgQLLl48WKZEsx2WYA+IOK7ge/xm/3XdwPf43f5PTzJdXcqUZw/MkzuXjwv8vQrXRO7Te3J472jMpLNhKODr19S+ibaImOHiKyfnZUHb8/KXH0I+w59aHrJxKxsnp+Vq/uLvKLzrM893XV9SW604rrp+yMWzyr7vJKyZVfCgsQJVNKulZRNXKCXqVAlcVVS9jKbTNSiSmKqpGyignybylQSVyVl32aziVlcSUyVlE1MgFQkFgGnEsVB/TIyVyeLZioeVdzYnijeX3DY+er+Gdk8r04en18nt11Xemh51FUZWfyecP4Tx91NFPv319muni43WmiXmW9rYUqfAH1AxHcD3+M3e7XvBr7Hn7539mRE5FSiaMg6Dj/r8xT1JeaBYssZJUffkOB8w1uvLk0IL0c9vSEs/7IeVTzj6OHnwYMHByHq2+CUDfX8eT0MqydbtmxBFjgpYNvV5z7gu4Hv8Zsd13cD3+N38s3bgUo7lyia8w/N4eQTb+rDz6dDYXvYuXA0sbv214SDcUHxU3qdLk4jR44Mqn348OGy1bfLbNmyBVngpIBtV9vOUUHYZbZsVBmX59m4bJxRsdhltmxUGVfn2ZhsjFFx2GW2bFQZl+fZuGycUbHYZbZsVBlX59mYbIxRcdhltmxUGeYhUCjgXKJozj+8T5+HaKZHjoUjiuZqZ3M3nHsau44m/tvhvNyzOSf/dDBfGHOXv396NnxqXtl4VZdFzjwZO3ZsUNf9+/eXrfO+ffuCZePGjStbhgXuCtAH9LnInu8Hvsdv9l7fDXyP39138GTX3LlE0XDaw8/mvMRnXzc/IjMaRK4b0DVRvPYKkadeEfnST5RcaL8Bd3FzfONomGyaC14G1nd9fXHZpD6fP39+ULUtW7bIwYMHS6q5bds22bt3bzB/3rx5JcuZ4b4AfUDEdwPf4zd7se8Gvsfv/jt5QiNw7atkbH3vfqyt46v5btLf5fzIsZxd1PH4cmtejf9aWO7j38+ps5fyHcvMH19+Nhesw7x++4muy7oU7MUT3ewmE+3y04vVRb60tbVVNTY2BtvQ38Cijh8/3lHuyJEjqqmpKVg2efJklc/XJs6ODSboj+bm5iBuH77Cjz6glO8Gvsdv3np8N/A9/nIfP3F8FhR/7pvnrk4ZU3EdgHPTl57Ny6efDKt+lb6Q96n7sjKg/dtYCoPZqq9mXrA9PPR8jR5hvP06kav01dD79be7/KT9sPOicRn5s8m1GVzNtN+qp7BOtSB/4oknZO7cuaK/61my2azMmjVL9JuG6B0k2LS5j+KuXbtk4sSJhVVJ9d87d+6UadOmiU4U5cSJE6mO1QRHH8CAPkAfoA+UvtXH8VnQV5/9pdHWYI6rGe6ZC3k1+ivhaOGSnaWjiYVxPfNKXv3K42FZM3pofm7+cpua/WjtRhLt9nWTBaNahY92WbUf9+zZo6ZMmaJ0B+3Ypk4a1cyZM5U+gbnam0v8+uL4LzJuFPqAUr4b+B6/2Qd9N/A9/uL34Tg+Cwo/8+3fxfVy5bmzI4oavuKptU2JuXjFnIl4y9XS8X3QFa+oghfE8V+FuRXOoUOHpL6+XsaMGSP2W1kqqDZFHRegD4j4buB7/GYX9t3A9/jjfBuP47O/VvF6lSjWCvFy601TZ7lcnCxDAAEEEEAAgVAgTZ/9tTkxj56CAAIIIIAAAggg4LwAiaLzTUgACCCAAAIIIIBAbQRIFGvjyloRQAABBBBAAAHnBUgUnW9CAkAAAQQQQAABBGojQKJYG1fWigACCCCAAAIIOC9Aouh8ExIAAggggAACCCBQGwESxdq4slYEEEAAAQQQQMB5ARJF55uQABBAAAEEEEAAgdoIkCjWxpW1IoAAAggggAACzguQKDrfhASAAAIIIIAAAgjURoBEsTaurBUBBBBAAAEEEHBegETR+SYkAAQQQAABBBBAoDYCJIq1cWWtCCCAAAIIIICA8wIkis43IQEggAACCCCAAAK1ESBRrI0ra0UAAQQQQAABBJwXIFF0vgkJAAEEEEAAAQQQqI0AiWJtXFkrAggggAACCCDgvACJovNNSAAIIIAAAggggEBtBEgUa+PKWhFAAAEEEEAAAecFSBSdb0ICQAABBBBAAAEEaiNAolgbV9aKAAIIIIAAAgg4L0Ci6HwTEgACCCCAAAIIIFAbARLF2riyVgQQQAABBBBAwHkBEkXnm5AAEEAAAQQQQACB2giQKNbGlbUigAACCCCAAALOC5AoOt+EBIAAAggggAACCNRGgESxNq6sFQEEEEAAAQQQcF6ARNH5JiQABBBAAAEEEECgNgIkirVxZa0IIIAAAggggIDzAiSKzjchASCAAAIIIIAAArURIFGsjStrRQABBBBAAAEEnBcgUXS+CQkAAQQQQAABBBCojQCJYm1cWSsCCCCAAAIIIOC8AImi801IAAgggAACCCCAQG0ESBRr48paEUAAAQQQQAAB5wXqnY+gggCefkXJxueVvHBOSf+6jIy6SuTeUeYxU8Fakl20ublZtm/fLgcOHJB+/fpJU1OTzJkzRyZNmpTsilexdhh0Yi5YsEAuXbok69at65zpwV++9wHf4zddHIPOHZ33AX8/Dzt7QS/+Up5Mn3kyp25a21byM+orbeqff5yrmYJuGlX8U4uNtba2qoULF5Zsy2y7rq5OLV68WOVytYuzFjFVuk4Muort3r076A8NDQ1dF6T4me99wPf4TdfGoOsOzvtA18/gvvo8LP7cN89dndyteQXif/10mCS+Z32bMgnjjhN5tf6nOfWrT4SJ4widQDafylewxu4X7avOsnTp0iApyGazasmSJWrr1q1q8+bNatGiRR3J48qVK7tfcQdLYtDZaC0tLaqxsdG7RNH3PuB7/GYPwID3gST0gb767O9s7dr9lfpE8Xs6KTQjiaP1yOEzr5Qmgx/6Tpgsfvz7tRlt64vOcuzYsWDU0GxrzZo1Jb1l+fLlQcIwaNAgdfbs2ZLlaZiBgVJr165Vy5YtU7Nnz1b19fUd/yD4MqLoex/wPX7zPoYB7wNJ6QN98dnfV5/dqU8Uf/8H4WjiPx6ITgS360Ry7qY2tWBbW03M+6KzrFq1KkgKRo0apdraSuM4d+6cGjJkSFBm/fr1NYkz7pVioNT48eM7ksPCfudLouh7H/A9fvMehAHvA0npA4XvwfbvuD8ne7p9Z656fqglLxPW52TOxpw2j572nlZBmakP5+RiTskF/fOdF8xnp8g9jdEXrMxoyMimuXXybzProlfqwNwdO3YEtdQjSaLPvyipsR5JlOnTpwfzzYUuaZwwEFm9erVs2LCh42fFihVpbOqyMfneB3yP33QMDHgfoA+UfYvs8QJnrnq+a0RGHnxKyWuXRJ7RCeHEoaWJ38bnwuV33piRK/RVzc2nlJxvE7nlHSI3DgrLn7moZO9p0YmkyPhrRG4aXLqeHmvG9MKjR48GW54wYULZGujRpiCB0MPyZcu4vAADkRkzZnRpwqFDh3Z5nvYnvvcB3+M3/RsD3gfoA9V/p3cmURyhE7qpw0V2vSTyqE4IoxLFTe2jh/eNDpO/ly6Eo4k369vgvKr//u3v5eXJl7sijhsi8g+/kJUxQ9xNGE+dOhUENWzYsK7BFTwbPlzj6enkyZMFc9PzJwbpacueRuJ7H/A9ftNvMOjp3pOe19EHqt+Wzhx6NqE/0J4APqrvhVg87X9VyfPnRG4YKDLt+nDpKxfCx7wu/sATeXnqFZEPvFPkd38uI/fcnJEh/UVaXhOZ/1heDujXuzpduBAGOnCgDr7MNGDAgGDJxYsXy5RwezYGbrdfNWrvex/wPX7ThzCoxp7k9jroA9VvP2dGFE3o80dm5M+eVPLieRFz8+zbruscBdzUnjyaG2hnM+H80+2J4rYTIu/oJ/L12Vm5fVjna069qeS3tufl4BmRZT/KyzfnlJ7fV33y6q9R3x+x2yutpGy3V5qAgpXEVUnZBIRGFbopUEm7VlK2m5uPvVglMVVSNvbAKqhAJXFVUraCKlA0ZoFK2rWSsjGHFevmnRpRHNQvI3N1smim4lFF840rZrq/fdTR/N2vILo/mJDpkiSa5TdcmZG/fF9YyBySPvyam6OK/fvroVE9XW600C4z39aSxgmDNLZqZTH53gd8j9/0Fgwq22fSWJo+UP1WLUilqr/yWqyx4/CzPk9RX+odbKLljJKjb4QXp9x6deeI4TVXdNZgrr4YJmoyo5JD28v95PWoEsmfN3jw4KCS+jY4ZSt7/rwehtWTLVu2oKMLbFw+GzjadFWrtu99wPf4TUfCoGq7k7Mrog9Uv+mcSxTN+YcNV4qceFMfftZXL5vJHnYuHE00868LT8szf+rRw+Ah8tf17ct+1urmiOLIkSODuA4fPhwZn5lpl9myZQs6usDGZeOMCsMus2WjyjDPXQHbrradoyKxy2zZqDKuzrMx2Rij4rDLbNmoMi7Ps3HZOKNiscts2agyzHNXwLarbeeoSOwyWzaqDPM6BZxLFM35h/fp8xDN9MixMLEzVzvru+GU3Cvx/ddnxI4jmvMay00vtg/EmSurXZzGjh0bVHv//v1lq79v375g2bhx48qWcXkBBi63XnXq7nsf8D1+04swqM6+5PJa6APVbz3nEkVDYA8/m/MSn33d/Oh7RzWYEcSuiZ55fnv7HWO+eTR6tHDrcSVn3xKp1y+dcG31gftijfPnzw82s2XLFjl48GDJJrdt2yZ79+4N5s+bN69keRpmYJCGVuxdDL73Ad/jN70Hg97tQ2l4NX2gBq3Y0690ift1dz8WfkfzR74bPj5yLPor+r5xJPwKv1vWtalNz3f9rueWM3k19Vvh6/94V/TrexunbjKToXb56e06i1/f2tqqGhsbg23ob2BRx48f7yhy5MgR1dTUFCybPHmyyue7GnQUdPwPDEobsLm5OWh3X77Cz/c+4Hv8Zg/AgPeBpPSB4s9989zVydmaf/FwmADetLZNjftqm2ptK58A/e3ezrK/vLFNme9/vn9Lm3rXV8IkcZ7+rueXW8u/vjeN21ed5fHHH1f19fVBYpDNZtUdd9yhpk2bFjw3ddD3UVR6VLE3oST+tRh0bSLfEkUTve99wPf46QNd3wPMM94H4vk87KvP/tIWr/4cZxPFMxfyanR7ordk59uPBv7zj3Pqw5vb1Kj215gEc8o329RnnsypC5dJMntL3pedZc+ePWrKlCkqk8l0JIgmaZw5c6bSJ+/2NhQnXo9BZzP5+AFhove9D/geP32g8z3A/MX7QDyfh3352d+1xav/LGNWqQPyZmptU3JIfxvLSH1HmaFF5zTWAkEnbSWrrTW5uRXOoUOHRI8wypgxY8R+K0tJRVI8A4MUN243Q/O9D/gev+kmGHRzZ0lxsbj6QByf/bVqRu8SxVpBlltvmjpLuRiZjwACCCCAAAKdAmn67HfyqufOpuAvBBBAAAEEEEAAgVoJkCjWSpb1IoAAAggggAACjguQKDregFQfAQQQQAABBBColQCJYq1kWS8CCCCAAAIIIOC4AImi4w1I9RFAAAEEEEAAgVoJkCjWSpb1IoAAAggggAACjguQKDregFQfAQQQQAABBBColQCJYq1kWS8CCCCAAAIIIOC4AImi4w1I9RFAAAEEEEAAgVoJkCjWSpb1IoAAAggggAACjguQKDregFQfAQQQQAABBBColQCJYq1kWS8CCCCAAAIIIOC4AImi4w1I9RFAAAEEEEAAgVoJkCjWSpb1IoAAAggggAACjguQKDregFQfAQQQQAABBBColQCJYq1kWS8CCCCAAAIIIOC4AImi4w1I9RFAAAEEEEAAgVoJkCjWSpb1IoAAAggggAACjguQKDregFQfAQQQQAABBBColQCJYq1kWS8CCCCAAAIIIOC4AImi4w1I9RFAAAEEEEAAgVoJkCjWSpb1IoAAAggggAACjguQKDregFQfAQQQQAABBBColQCJYq1kWS8CCCCAAAIIIOC4AImi4w1I9RFAAAEEEEAAgVoJkCjWSpb1IoAAAggggAACjguQKDregFQfAQQQQAABBBColQCJYq1kWS8CCCCAAAIIIOC4AImi4w1I9RFAAAEEEEAAgVoJkCjWSpb1IoAAAggggAACjguQKDregFQfAQQQQAABBBColQCJYq1kWS8CCCCAAAIIIOC4AImi4w1I9RFAAAEEEEAAgVoJkCjWSpb1IoAAAggggAACjguQKDregFQfAQQQQAABBBColUB9rVachPWefFPJd15Q3a7K/JEZGT4w0+3ySSzY3Nws27dvlwMHDki/fv2kqalJ5syZI5MmTUpidWtSJww6WRcsWCCXLl2SdevWdc704C/f+4Dv8Rd3cR/3A/qACAbFe0IPn6sUT82n8uqmtW3d/vnRS/mqa+hmMZlql5+qb0SvsLW1VS1cuLDLdux26+rq1OLFi1Uul6vFphOzTgy6NsXu3buD/tDQ0NB1QYqf+d4HfI8/qmv7th/QB5LxeWg/fwsfo/qnC/PEhUr2tI5HzubVn+3OXfbnD36QCxLJW9a1qRfecDdRXLp0aZAUZLNZtWTJErV161a1efNmtWjRoo7kceXKlT2ldOJ1GHQ2U0tLi2psbPQuUfS9D/gef+ceEP7l435AH1AqCQaFCaL9u7h/uvI81Yni2zVCPp9XH90Wjjg+fLQ2o222gxQ+vl29Kl1+7NgxZUYNzTbWrFlT8vLly5cHywYNGqTOnj1bsjwNMzBQau3atWrZsmVq9uzZqr6+vuMfBF9GFH3vA77Hb9/HfN4P6ANKJcWg8DPf/m37qGuPXieKf7M3HE388z21SRJNZ7AdpPCx2p1k1apVwXZGjRql2traSlZ/7tw5NWTIkKDM+vXrS5anYQYGSo0fPz6yv/mSKPreB3yP376P+bwf0AeUSopB4We+/dv2Udcenbnq+aGWvExYn5M5G3PaPHrae1oFZaY+nJOLOfOZWX56TF/ksuqAkp8fLvKpSW5fwLJjx44gUD2SJHpksSRoPZIo06dPD+abC13SOGEgsnr1atmwYUPHz4oVK9LY1GVj8r0P+B6/7Rg+7wf0AREM7J5QvUdnrnq+a0RGHnxKyWuXRJ7RCeHEoaXJ3cbnwuV33piRK+pKl1u2N95S8und+eDp8vdmpS5bvqx9TZIfjx49GlRvwoQJZaup/8sOEgg9LF+2jMsLMBCZMWNGlyYcOnRol+dpf+J7H/A9ftu/fd4P6AMiGNg9oXqPzowojhickal69M9Mj+qEMGra1H4rnPtGXz7x+/x+Ja9cELn75oxMuPbyZaO2k7R5p06dCqo0bNiwslUbPjzEO3nyZNkyLi/AwOXWq07dfe8DvsdfnV7k9lroAyIYVL8PO5MomtAfaE8AH32+NFHc/6qS58+J3DBQZNr15aGOvqHkXw8rqdf54ZKJ7ieJJtILF3TWq6eBA3XwZaYBAwYESy5evFimhNuzMXC7/apRe9/7gO/xV6MPub4O+gCfh7Xow04liuaG2AP1KXgvnhd5+pWuyeKm9uTx3lEZyWbKJ4B/9XRe3tJHne/T5UZdVb5cLbBrtU59f8Rur7qSst1eaQIKVhJXJWUTEBpV6KZAJe1aSdlubj72YpXEVEnZ2AOjAt0WqKRdKynb7QokoGAlcVVSNgGhxVYFpxLFQf0yMlcni2YqHlXc2J4o3n+Zw86nLyjZ/GJo/XaHp8NSbvzu379/UNHLjRbaZebbWtI4YZDGVq0sJt/7gO/xV9Zb0lmaPiCCQfX7tlOJogm/4/CzPk9RX2IeiLScUXL0DZHx14jcenX5UcJvH1NiLoY2h6ft+Y7VJ+37NQ4ePDjYqL4NTtmNnz+vh2H1ZMuWLejoAhuXzwaONl3Vqu17H/A9/qp1JIdXRB/o/Izjs6B6Hdm5RNGcf9hwpciJN/Xh59MhhD3sfLnRRFNy/ZEwsTQXsWQuc3i6erx9s6aRI0cGGzp8+HDZDdpltmzZgo4usHHZOKPCsMts2agyzHNXwLarbeeoSOwyWzaqjKvzbEw2xqg47DJbNqoM89wVsO1q2zkqErvMlo0q4/I8G5eNMyoWu8yWjSrDvE4B5xJFc/6hOb/QTI/oEUIzmaudzd1w7mksP5r4X68rOXAmKC4fuky5sIRbv8eOHRtUeP/+/WUrvm/fvmDZuHHjypZxeQEGLrdederuex/wPf7q9CK310IfEMGg+n3YuUTRENjDz+a8xGd1Avjs6/oecg0i1w0onyju01dFm8lc7WwOUadpmj9/fhDOli1b5ODBgyWhbdu2Tfbu3RvMnzdvXsnyNMzAIA2t2LsYfO8Dvsffu96TjlfTB0QwqEFfdu2rZGx9734s/I7mj3w3fHzk2OW/hu9zT4Vf1zfrkdKvuLPrrMWjbjKToXb5qfZ2WltbVWNjY7AN/Q0s6vjx4x2bOHLkiGpqagqWTZ48WZnvt07jhEFpqzY3Nwft7stX+PneB3yPv3QPCOf4tB/QB5RKikHx57557urkbM2/eDhM/G5a26bGfbVNtbZdPgH6rW1hQvmxHelLFE3ne/zxx1V9fX2QGGSzWXXHHXeoadOmBc9NB9X3UVR6VNHVftqtemPQlcmnD0gbue99wPf4bT8ofPRtP6APJOPzkESxcC+M6e8zF/Jq9FfC5G/JzsuPJpoqTns4LPu3e9++bDVD6svOsmfPHjVlyhSlL9TpSBBN0jhz5kylT96tZliJXRcGnU3j2wekjdz3PuB7/LYf2Ecf9wP6gFJxG/TlZ7/t67V6zJgV64CYaiQQdXV1rcnNrXAOHTokeoRRxowZI/ZbWWoUYiJXi0Eim6VPK+V7H/A9/j7tbAndGH1AJC6DOD77a9UNSRRrJdu+3jR1lhpTsXoEEEAAAQRSIZCmz34nr3pORS8iCAQQQAABBBBAIOECJIoJbyCqhwACCCCAAAIIxCVAohiXPNtFAAEEEEAAAQQSLkCimPAGonoIIIAAAggggEBcAiSKccmzXQQQQAABBBBAIOECJIoJbyCqhwACCCCAAAIIxCVAohiXPNtFAAEEEEAAAQQSLkCimPAGonoIIIAAAggggEBcAiSKccmzXQQQQAABBBBAIOECJIoJbyCqhwACCCCAAAIIxCVAohiXPNtFAAEEEEAAAQQSLkCimPAGonoIIIAAAggggEBcAiSKccmzXQQQQAABBBBAIOECJIoJbyCqhwACCCCAAAIIxCVAohiXPNtFAAEEEEAAAQQSLkCimPAGonoIIIAAAggggEBcAiSKccmzXQQQQAABBBBAIOECJIoJbyCqhwACCCCAAAIIxCVAohiXPNtFAAEEEEAAAQQSLkCimPAGonoIIIAAAggggEBcAiSKccmzXQQQQAABBBBAIOECJIoJbyCqhwACCCCAAAIIxCVAohiXPNtFAAEEEEAAAQQSLkCimPAGonoIIIAAAggggEBcAiSKccmzXQQQQAABBBBAIOECJIoJbyCqhwACCCCAAAIIxCVAohiXPNtFAAEEEEAAAQQSLkCimPAGonoIIIAAAggggEBcAiSKccmzXQQQQAABBBBAIOECJIoJbyCqhwACCCCAAAIIxCVAohiXPNtFAAEEEEAAAQQSLkCimPAGonoIIIAAAggggEBcAiSKccmzXQQQQAABBBBAIOECJIoJbyCqhwACCCCAAAIIxCVAohiXPNtFAAEEEEAAAQQSLlCf8PpVrXrn3lLy9SNKWl4TefWCksarMvLuq0XuvjkjA+szVdtO3Ctqbm6W7du3y4EDB6Rfv37S1NQkc+bMkUmTJsVdtT7bvu8Gvsdf3NEWLFggly5dknXr1hUv8uK5r/H7vh/4Hr/ZuTGo0luc8mD6zvN5NWF9m7ppbenP+7/VpnaeytdMQTeTKv6pxcZaW1vVwoULS7Zltl1XV6cWL16scrlcLTadmHX6buB7/FEdcffu3cE+0dDQELU49fN8jN/3/cD3+M1OnQSD4s9989zVyd2ad1P8wOm8umVdmCDev6VNbX4hr55+Ja8+vz+nPrAhnD9RJ5GvXqhNsthXnWXp0qXBB2I2m1VLlixRW7duVZs3b1aLFi3qSB5XrlzZTTU3i/lu4Hv8xb22paVFNTY2epso+hq/7/uB7/Gb94EkGPTVZ3/x+14tnqc+UfzUD3PBSOIHH2tTb+W6JoPnLuXVz+sRRTPS+I8HajPa1hed5dixY8GoodnWmjVrSvrJ8uXLgw/LQYMGqbNnz5YsT8MM3w18j9/24bVr16ply5ap2bNnq/r6+o5/knwZUfQ9ft/3A9/jN+8DSTHoi89++75X68fUJ4pzN4WJ4D8djE4E/7A5TCQ/+YPo5b1tgL7oLKtWrQo+EEeNGqXa2tpKqnzu3Dk1ZMiQoMz69etLlqdhhu8Gvsdv+/D48eM7ksPCfc+XRNH3+H3fD3yP37wPJMWg8P3H/m3fp1x7dOaq54da8jJhfU7mbMxp8+hp72kVlJn6cE4u5sznhcjNg8MLVVrbol/T2r660VdFL3dh7o4dO4Jq6lEU0ecjllRZjyTK9OnTg/nmQpc0Tr4b+B6/7dOrV6+WDRs2dPysWLHCLvLi0ff4fd8PfI/f7OQYVP+tzplE8a4RGXntkgRXLT+jE8KoaeNzKijz/uEZuaIuTBBn3xSW/NYxJebK58Lp5JtKtp8I582+yd0rn48ePRqENWHChMLwuvytRxqC53pYvsv8tDzx3cD3+G0/njFjhnzwgx/s+PnFX/xFu8iLR9/j930/8D1+s5NjUP23OmdujzNCjwxOHS6y6yWRR3VCOHFoaWK36YUw6btvdOeyD+nb3zz1isi/P6tk7mN5WXBrRm4YmJGtOkF8TJd/U480/s/3ZuTnrul8TfWZa7vGU6dOBRsYNmxY2Q0NH67x9HTy5MmyZVxe4LuB7/G73Hepe/UEfN8PfI/f9CQMqrc/2TU5kyiaCj+gE8BdLyl59HklfzrZhhA+7n9VyfPnRCeBItOu71xWn83IZ28XOfaGkh06R/pfe0wyGSaUptR/a8zIR97tbpJoYrhw4YJ5kIEDdfBlpgEDBgRLLl68WKaE27N9N/A9frd7L7WvloDv+4Hv8Zt+hEG19qbO9Thz6NlUef5IfXNsfQrei+dFnn6lM9kzyzbp5NFM947KSDbTmfid1jfX/s3t+SBJNEejp+hBt3t1cjhpaFBcHtaHpGdtyOsks+v6wqVu/Nb3R+x2RSsp2+2VJqBgJXFVUjYBoXWrCpXEVEnZbm2cQggkRKCSvl1J2YSE97bVqCSmSsq+7YYTVKCSuCopm6AQ+7wqTo0oDuqXkbk6Wfzm0XBU8bbrOhPCje2J4v0Fh52N5m/pJHHvaZFb9bewrJme1d/G0vmaH72sZNH38vKCTjw/9cO8fOWO0gtB+rxFerDB/v37B6+63GihXWa+rSWNk+8Gvsefxj5NTJUL+L4f+B6/6TEYVL7fvN0rnBpRNMGYw89mMucp6kvMg79bzig5+obI+GtMQtiZCL7UqoIk0RT656Ik0cy7fVhG/n5aSPBDfe5ja5ubo4qDBw824Yi+DU7wGPXr/HmdDevJlo0q4/I8G5evBr7H73Lfpe7VE/B9P/A9ftOTMKje/mTX5FyiaM4/bLhS5MSb+vCzHik0kz3sXDyauK39iuZGfeubWwoSyPBV4e/pN+iOpQfZLuX1hTI/K1zizt8jR44MKnv48OGylbbLbNmyBR1dYOOycUaFYZfZslFlXJ1nY7IxRsVhl9myUWWYh4DLArZv274eFYtdZstGlXF1no3JxhgVh11my0aVcXmejcvGGRWLXWbLRpVhXqeAc4miOf/wPn0eopke0ecXmslc7WzOP7xHn3sYNbXfKSdqkRS+ouDUxsiySZ05duzYoGr79+8vW8V9+/YFy8aNG1e2jMsLfDfwPX6X+y51r56A7/uB7/GbnoRB9fYnuybnEkVTcXv42ZyX+Ozr5kdkRoPIdQMK0z6RCdeGz4+clbIXq5jb7Zx7K+R4z7WWxa3H+fPnBxXesmWLHDx4sKTy27Ztk7179wbz582bV7I8DTN8N/A9/jT0YWLovYDv+4Hv8ZsehEHv96OSNbj2VTK2vnfr724239H8ke+Gj48cK/0KPvPdznc+Gi43X+X3/Btdv+v5x6/m1fvbv+v5N7eWfvWd3VZvHjW4Gfbs8tOb9UW9trW1VTU2Ngbb0N/Aoo4fP95R7MiRI6qpqSlYNnnyZJXPdzXoKOj4H74b+B5/ue7b3Nwc9H1fvsKv2MG3+H3fD3yP3/T/pBgUf+6b565OGVNxHYBz05eezcunnwyrfpU+x/Cp+7IyIOIY80/PKpmvb7R9Xt9Yu78eP32fvu/0jVdm5Dl9O5wnXxYx3/Rn7r24eV5Wri0akawGSibieHYtyJ944gmZO3eu6O96lmw2K7NmzRK9w4j+oAjCMPdR3LVrl0ycOLEaYSVyHb4b+B5/VKfcuXOnTJs2TXSiKCdOnIgqkup5Psbv+37ge/xmh06CQV999vfJG5irGe6ZC3k1+ivhaOGSnaWjiYVxHT+XV4t1mcYvh+XNSKT5uWVdm3pwT069drF2o2y6EYMRjcLHwrpV8+89e/aoKVOmKN1BO7apk0Y1c+ZMpU/ereamErsu3w18j7+4Y/o2okb8oYDv+4Hv8ZteELdB4We+/bt4/3TlubMjihq+4qktr+S4vkvMqVaRd+orp28cJF1uzl3xCrvxgjj+qzC3wjl06JDU19fLmDFjxH4rSzeqm5oivhv4Hn9qOjKB9ErA9/3A9/hN54nLII7P/l7tLJd5sVeJ4mUcarYoTZ2lZkisGAEEEEAAgRQJpOmz38mrnlPUlwgFAQQQQAABBBBIrACJYmKbhoohgAACCCCAAALxCpAoxuvP1hFAAAEEEEAAgcQKkCgmtmmoGAIIIIAAAgggEK8AiWK8/mwdAQQQQAABBBBIrEB9YmuW4opFXQ1VrXD1fZmqtSrWgwACCCCAQGoFavlZnCY0RhTT1JrEggACCCCAAAIIVFGARLGKmKwKAQQQQAABBBBIkwCJYppak1gQQAABBBBAAIEqCpAoVhGTVSGAAAIIIIAAAmkS4Cv80tSaxIIAAggggAACCFRRgBHFKmKyKgQQQAABBBBAIE0CJIppak1iQQABBBBAAAEEqihAolhFTFaFAAIIIIAAAgikSYBEMU2tSSwIIIAAAggggEAVBUgUq4jJqhBAAAEEEEAAgTQJkCimqTWJBQEEEEAAAQQQqKIAiWIVMVkVAggggAACCCCQJgESxTS1JrEggAACCCCAAAJVFCBRrCImq0IAAQQQQAABBNIkQKKYptYkFgQQQAABBBBAoIoCJIpVxGRVCCCAAAIIIIBAmgRIFNPUmsSCAAIIIIAAAghUUYBEsYqYrAoBBBBAAAEEEEiTAIlimlqTWBBAAAEEEEAAgSoKkChWEZNVIYAAAggggAACaRIgUUxTaxILAggggAACCCBQRQESxSpisioEEEAAAQQQQCBNAiSKaWpNYkEAAQQQQAABBKooQKJYRUxWhQACCCCAAAIIpEmARDFNrUksCCCAAAIIIIBAFQVIFKuIyaoQQAABBBBAAIE0CZAopqk1iQUBBBBAAAEEEKiiAIliFTFZFQIIIIAAAgggkCYBEsU0tSaxIIAAAggggAACVRQgUawiJqtCAAEEEEAAAQTSJECimKbWJBYEEEAAAQQQQKCKAiSKVcRkVQgggAACCCCAQJoESBTT1JrEggACCCCAAAIIVFGARLGKmKwKAQQQQAABBBBIkwCJYppak1gQQAABBBBAAIEqCpAoVhGTVSGAAAIIIIAAAmkSIFFMU2sSCwIIIIAAAgggUEWB/x9fdTd+2zjIIwAAAABJRU5ErkJggg==" alt="" width="267" height="215" />

                     示例图                            图的邻接表存储方式                       图的邻接矩阵存储方式

        

三、实现方式

[伪代码]
1. 初始化队列Q；visited[n] = ；
. 访问顶点v；visited[v] = ；
. 顶点v入队列Q；
. while（队列Q非空）
        v = 队列Q的对头元素出队；
        w = 顶点v的第一个邻接点；
        while（w存在）
            如果w未访问，则访问顶点w；
            visited[w] = ；
            顶点w入队列Q；
            w = 顶点v的下一个邻接点。

1、邻接表非递归实现

广度优先遍历（BFS）的非递归遍历可以使用队列这个数据结构来实现。写代码前我画了一个非递归遍历入队出队的流程图，如下所示。

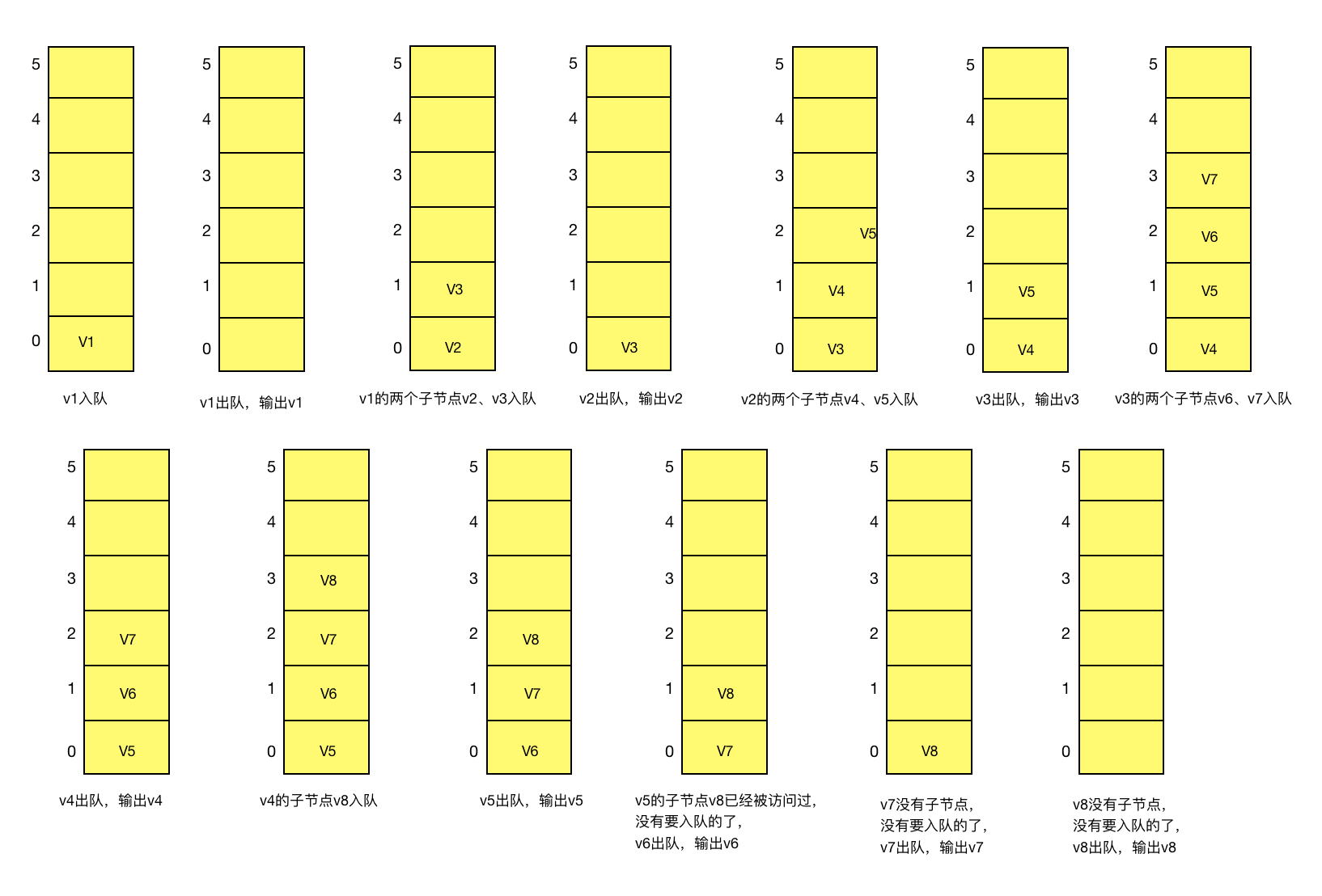
<?php
/**
 * 图的广度优先遍历
 * 图的存储结构--邻接表
 */

//实现连通图的广度优先搜索
class Node{
    public $value = null;
    public $next = array();//存储下一个节点位置的数组

    public function __construct($value = null){
        $this->value = $value;
    }
}

class Graph {
    // 记录节点是否已被遍历
    public $visited = [];
    // 图的邻接表数组
    public $graph = [];

    /**
     * 为顶点添加邻接点
     * @param $vertex 顶点v
     * @param $adjvex 顶点v的邻接点
     */
    public function addVertex($vertex, $adjvex)
    {
        $this->graph[$vertex][] = $adjvex;
    }

    /**
     * 非递归
     * @param $v 传入的是第一个需要访问的顶点
     */
    public function breadthFirstSearch($v) {
        // 初始化节点遍历标记
        $vertices = array_keys($this->graph);
        foreach ($vertices as $vertex) {
            $this->visited[$vertex] = 0;
        }
        $this->visited[$v] = 1;     // 设置当前顶点访问过
        $queue[] = $v;
        while (!empty($queue)) {    // 若当前队列不为空
            $current = array_shift($queue);     // 将队对元素出队列
            echo $current . PHP_EOL;            // 打印顶点
            for ($i = 0; $i < count($this->graph[$current]); $i++) { // 查找该顶点的相邻顶点
                $curChildNode = $this->graph[$current][$i];
                if ($this->visited[$curChildNode] == 0) {   // 若是未访问过就处理
                    $queue[] = $curChildNode;               // 将找到的此顶点入队列
                    $this->visited[$curChildNode] = 1;      // 将找到的此顶点标记为已访问
                }
            }
        }
    }
}

// 测试
$vertices = ['v1', 'v2', 'v3', 'v4', 'v5', 'v6', 'v7', 'v8'];
$g = new Graph();
$g->addVertex('v1', 'v2');
$g->addVertex('v1', 'v3');
$g->addVertex('v2', 'v1');
$g->addVertex('v2', 'v4');
$g->addVertex('v2', 'v5');
$g->addVertex('v3', 'v1');
$g->addVertex('v3', 'v6');
$g->addVertex('v3', 'v7');
$g->addVertex('v4', 'v2');
$g->addVertex('v4', 'v8');
$g->addVertex('v5', 'v2');
$g->addVertex('v5', 'v8');
$g->addVertex('v6', 'v3');
$g->addVertex('v6', 'v7');
$g->addVertex('v7', 'v3');
$g->addVertex('v7', 'v6');
$g->addVertex('v8', 'v4');
$g->addVertex('v8', 'v5');

// 非递归
$g->breadthFirstSearch($vertices[0]);

2、邻接矩阵非递归实现

<?php
/**
 * 图的广度优先遍历
 * 图的存储结构--邻接矩阵
 */
class Graph {
    // 存储节点信息
    public $vertices;
    // 存储边信息
    public $arcs;
    // 图的节点数
    public $vexnum;
    // 记录节点是否已被遍历
    public $visited = [];

    // 初始化
    public function __construct($vertices) {
        $this->vertices = $vertices;
        $this->vexnum = count($this->vertices);
        for ($i = 0; $i < $this->vexnum; $i++) {
            for ($j = 0; $j < $this->vexnum; $j++) {
                $this->arcs[$i][$j] = 0;
            }
        }
    }

    // 两个顶点间添加边(无向图)
    public function addEdge($a, $b) {
        if ($a == $b) { // 边的头尾不能为同一节点
            return;
        }
        $this->arcs[$a][$b] = 1;
        $this->arcs[$b][$a] = 1;
    }

    // 非递归
    public function breadthFirstSearch() {
        // 初始化节点遍历标记
        for ($i = 0; $i < $this->vexnum; $i++) {
            $this->visited[$i] = 0;
        }
        $queue = [];
        for ($i = 0; $i < $this->vexnum; $i++) { // 对每一个顶点做循环
            if (!$this->visited[$i]) {      // 若是未访问过就处理
                $this->visited[$i] = 1;     // 设置当前顶点访问过
                echo $this->vertices[$i] . PHP_EOL;   // 打印顶点
                $queue[] = $i;              // 将此顶点入队列
                while (!empty($queue)) {    // 若当前队列不为空
                    $curr = array_shift($queue);    // 将队对元素出队
                    for ($j = 0; $j < $this->vexnum; $j++) {
                        if ($this->arcs[$curr][$j] == 1 && $this->visited[$j] == 0) {
                            $this->visited[$j] = 1; // 将找到的此顶点标记为已访问
                            echo $this->vertices[$j] . PHP_EOL;   // 打印顶点
                            $queue[] = $j;          // 将找到的此顶点入队列
                        }
                    }
                }
            }
        }
    }
}

// 测试
$vertices = ['v1', 'v2', 'v3', 'v4', 'v5', 'v6', 'v7', 'v8'];
$graph = new Graph($vertices);
$graph->addEdge(0, 1); // v1 v2
$graph->addEdge(0, 2); // v1 v3
$graph->addEdge(1, 3); // v2 v4
$graph->addEdge(1, 4); // v2 v5
$graph->addEdge(2, 5); // v3 v6
$graph->addEdge(2, 6); // v3 v7
$graph->addEdge(4, 7); // v5 v8
$graph->addEdge(3, 7); // v4 v8

$graph->breadthFirstSearch();