Luogu P5603 小C与桌游【贪心+拓扑排序】

【Description】https://www.luogu.com.cn/problem/P5603

\(\;\)

题意可以简化为：一个不保证联通，n个点，m条边的DAG（有向无环图），构造一个拓扑序S。

求：\(\sum_{i=1}^n f(i)\)的\(Max,Min\)

其中\(f(i)\)的定义：

\[f(i)=
\begin{cases}
1\;\;\;\;S(1\;to\;i-1)<S(i) \\
0\;\;\;\;other
\end{cases}
\]

【Sample Input】

3 2

1 2

1 3

【Sample Output】

3

2

\(\;\)

\(\;\)

先考虑\(Max\)？

假设现在所有入度为0的点组成的集合为\(\{S_1,S_2,\cdots,S_k \;\;\;\}\;(S_1<S_2<\cdots <S_k)\)

可以贪心地考虑，目前选择\(S_1\)是最优的。

感性证明？

假设我们选择了\(S_r\)，则\(S_1,\cdots,S_{r-1}\)在以后一定不会对答案产生贡献了。

而我们选择\(S_r\)唯一的好处就是：\(S_r\)可能是目前我们已选择中的最大值，会产生1的贡献

那我们完全可以先选择一个比\(S_r\)小的数\(S_p\)，这样\(S_p\)也有可能产生贡献，而对\(S_r\)的是否贡献没有影响，会更优。

用一个优先队列（小根堆）实现即可。

\(\;\)

\(\;\)

考虑\(Min\)

接着上面的思路？

选择\(S_k\)是不是最优的？

举个反例：



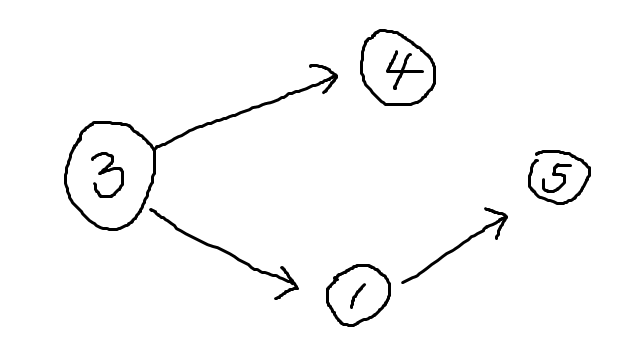
在这个例子中，按照原先的思路是3-4-1-5，答案为3。

而选择3-1-5-4，答案为2。显然更优。

所以我们得到一个新的思路，只要有小于目前最大值的，就选，否则选最大的那一个。

感性证明？

因为小于目前最大值的点不管什么时候，都不会对答案产生贡献了，所以我们先把它们选了再说。

而这样的好处就是：可以扩展出更多的点，这样就更容易创造一个更优的方法。

例子中：选了1后，我们扩展到了5这个点，就可以使4不产生贡献。

否则如果我们不选1的话，只能选择4，这样可能导致不是最优解。

\(\;\)

\(Code:\)

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
const int N=500010;
int n,m,ind[N],bind[N];
vector<int> g[N];
priority_queue<int> q;
priority_queue<int,vector<int>,greater<int> > Q;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        g[u].push_back(v);
        ind[v]++;
    }
    for(int i=1;i<=n;i++)
    {
    	bind[i]=ind[i];
        if(!ind[i])
        {
            Q.push(i);
        }
    }
    int maxn=0,res1=0,res2=0;
    while(!Q.empty())
    {
        int u=Q.top(); Q.pop();
        if(u>maxn)
        {
            res1++;
            maxn=u;
        }
        for(int i=0;i<g[u].size();i++)
        {
            int v=g[u][i];
            if(!(--ind[v]))
            {
                Q.push(v);
            }
        }
    }
    printf("%d\n",res1);

    for(int i=1;i<=n;i++)
    {
    	if(!bind[i])
    	{
    	    q.push(i);
	}
    }
    while(!q.empty())
    {
	while(!q.empty())
	{
	    int u=q.top();
	    q.pop();
	    if(u>maxn)
	    {
		res2++;
		maxn=u;
	    }
	    tt.push(u);
	}
	while(!tt.empty())
	{
	    int u=tt.front();
	    tt.pop();
            for(int i=0;i<g[u].size();i++)
	    {
		int v=g[u][i];
		if(!(--bind[v]))
		{
		    if(v<maxn)
		    {
		        tt.push(v);
		    }
		    else q.push(v);
		}
	    }
        }
    }
    printf("%d",res2);
    return 0;
}