洛谷 P3808 【模板】AC自动机（简单版） 题解

原题链接

前置知识：

字典树。（会 \(\texttt{KMP}\) 就更好）

显然呢，本题用 字典树 和 \(\texttt{KMP}\) 无法解决问题。

所以我们发明了一个东西： \(\texttt{AC}\) 自动机！

自动AC就算了吧

首先，我们给这些串建字典树。

建完之后，我们求 失配指针 。

这是干嘛的？求完再说。

它表示以 \(i\) 节点为 结尾 的串的 后缀 有最大公共长度的 前缀的 结尾 编号.

可能有点绕，但是字符串匹配算法，一开始就是雾里云里，后来就是拨云见雾。

引用一张洛谷题解上的图吧。

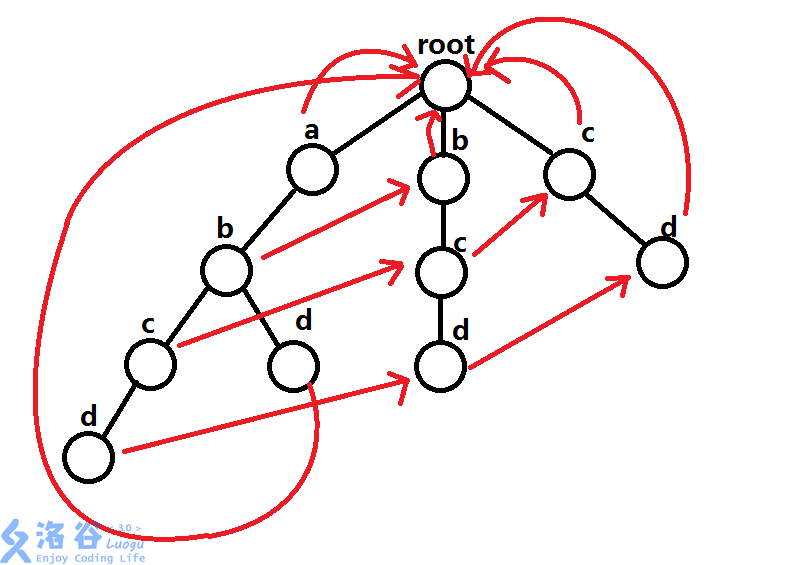
然后，比方说第 \(3\) 层的 \(c\).

首先，以它结尾的后缀有： \(\texttt{c}\),\(\texttt{bc}\),\(\texttt{abc}\).

显然，从根开始的前缀（不含根）找不到 \(\texttt{abc}\).

但是，我们找到了 \(\texttt{bc}\).

所以，就指向了 \(\texttt{bc}\) 中的 结尾 编号的 \(c\) 的位置。

余下同理，读者自行推理。

下面，我们假设这个图的只有每个叶子节点都是一个单词的末尾。那么，假设我们要找在 \(\texttt{abcde}\) 中的次数，一开始 \(ans = 0\).流程为：

首先一路往下，到 \(d\) 之后发现 \(e\) 没了。这时 \(ans \gets ans+1\)，即 \(ans = 1\).

这时我们创建一个空的 \(e\). 并且，对每个 \(e\) 也求一下 失配指针 ：

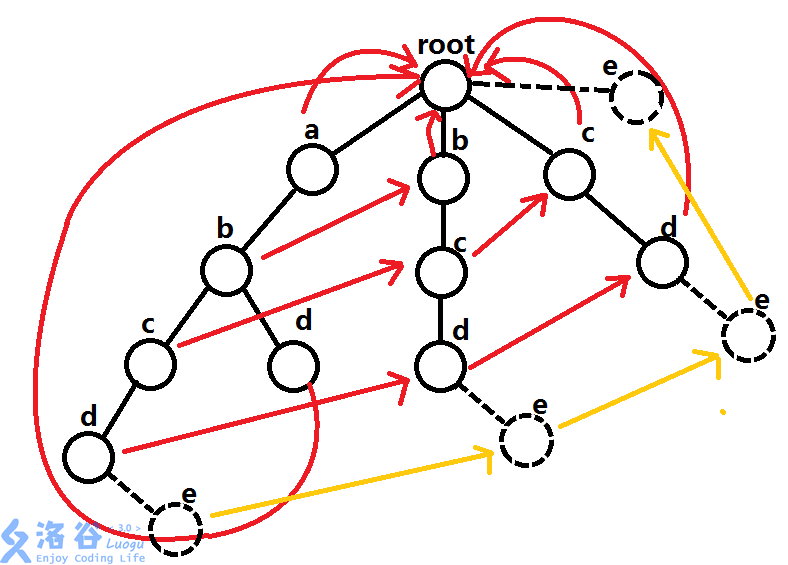
然后，你走到了第二叉的“空节点” \(e\).

然后，你发现：由于失配指针的性质， \(e\) 上面这一段肯定在 \(\texttt{abcd}\) 中出现过（因为后缀和前缀匹配，而长度递减），所以也在原串中出现过。

然后， \(ans \gets ans+1\)，即 \(ans = 2\).

接着，你又走到第三叉的“空节点” \(e\).

同样的道理，\(ans \gets ans+1\)，即 \(ans = 3\).

接着，你发现当前的 \(e\) 指向根，于是迫不及待地走向了根。

然后你发现当前节点编号是 \(0\)，结束。

\(ans = 3\)，没有一点毛病，不得不承认这个算法很妙。

可是怎么求 \(\texttt{Fail}\) （失配指针） 呢？

显然，如果父亲节点有了失配指针，你只需比较 你自己 和 父亲失配指针的那一位 ，相同则指过去，不然呢就指根。

这是因为，父亲节点以上全部匹配，如果你自己也匹配就完事了；否则呢，就不匹配了。

你会发现，第 \(i\) 层的所有指针需要 \(i-1\) 层。所以宽搜！

时间复杂度：\(O(n)\).（常数较大，需要提高效率）

实际得分：\(100pts\).

#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;

const int N=1e6+1;

inline int read(){char ch=getchar();int f=1;while(ch<'0' || ch>'9') {if(ch=='-') f=-f; ch=getchar();}
	int x=0;while(ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;}

struct tree {
	int fail,end; //失配指针，单词个数
	int nxt[26];
};
tree t[N];
int cnt=0;

inline void build_tree(string s) {
	int p=0;
	for(int i=0,tt;i<s.length();i++) {
		tt=s[i]-'a';
		if(!t[p].nxt[tt]) t[p].nxt[tt]=++cnt;
		p=t[p].nxt[tt];
	} t[p].end++;
} //建树

queue<int>q;
inline void getFail() {
	for(int i=0;i<26;i++)
		if(t[0].nxt[i]) {
			t[t[0].nxt[i]].fail=0;
			q.push(t[0].nxt[i]);
		} //根节点的儿子直接标记
	while(!q.empty()) {
		int now=q.front(); q.pop();
		for(int i=0;i<26;i++)
			if(t[now].nxt[i]) {
				t[t[now].nxt[i]].fail=t[t[now].fail].nxt[i];
				q.push(t[now].nxt[i]);
			} else t[now].nxt[i]=t[t[now].fail].nxt[i];
	}	//宽搜
}

inline int AC(string s) {
	int p=0,ans=0;
	for(int i=0,tt;i<s.length();i++) {
		tt=s[i]-'a'; p=t[p].nxt[tt];
		for(int j=p;j && t[j].end!=-1;j=t[j].fail) {
			ans+=t[j].end;
			t[j].end=-1; //为了防止一个子树被走多次
		} //只要不为空，就一直记录
	} return ans;
}

int main(){
	int n=read(); string s;
	while(n--) {
		cin>>s;
		build_tree(s);
	} t[0].fail=0; //初始化
	getFail();
	cin>>s; int x=AC(s);
	printf("%d\n",x);
	return 0;
}