Andrew Ng机器学习公开课笔记 -- Generative Learning algorithms

网易公开课，第5课
notes，http://cs229.stanford.edu/notes/cs229-notes2.pdf

学习算法有两种，一种是前面一直看到的，直接对p(y|x; θ)进行建模，比如前面说的线性回归或逻辑回归，这种称为判别学习算法（discriminative learning algorithms）

另外一种思路，就是这里要谈的，称为生成学习算法（generative learning algorithms），区别在于不会直接对p(y|x; θ)进行建模，而是对p(x|y) (and p(y))进行建模，然后用bayes定理算出p(y|x)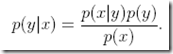
 
不像判别方法，给定x就能通过训练的模型算出结果
比如逻辑回归中，通过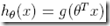

而生成学习算法的思路是这样的，由于需要对p(x|y)进行建模，x是连续的，但对于分类问题y是离散的，比如取值0或1
我们做的是，分别对每种y的情况进行建模，比如判断垃圾邮件，那么分别对垃圾和正常邮件进行建模，得到
p(x|y = 0) models 和 p(x|y = 1) models
而p(y) (called the class priors)往往是比较容易算出的
当来一个新的x时，需要计算每个y的p(y|x)，并且取概率最大的那个y
这里由于只需要比较大小，p(x)对于大家都是一样的，不需要算

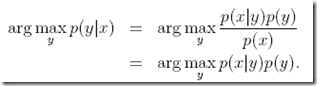
所以对于任意生成学习算法，关键就是要学习出
p(x|y = 0) models 和 p(x|y = 1) models

 

Gaussian discriminant analysis

首先学习的一个生成算法就是GDA，高斯判别分析
不解为何生成算法要叫判别。。。

多项高斯分布
对于这个算法，首先要假设p(x|y)符合多项高斯分布（multivariate normal distribution），区别于一般的高斯分布，参数μ是一维的，而多项高斯分布参数是n维的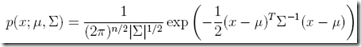

其中，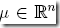
，mean vector，是个n维的向量
，covariance matrix，是个n×n的矩阵
关于这个分布，课件里面讲的很详细，还有很多图，参考课件吧
其实只要知道这个分布也是一个bell-shape curve，μ会影响bell的位置（平移）
而covariance matrix会影响bell的高矮，扁圆的形状

The Gaussian Discriminant Analysis model
继续讲这个模型
前面说了对于生成学习算法，关键就是要找出p(x|y = 0)，p(x|y = 1)和p(y)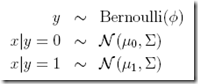
 
好理解吗，y取值0或1，一定是伯努利分布，而p(x|y)根据前面假设一定是符合多项高斯分布，所以有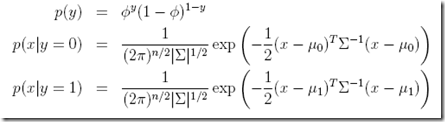

现在问题是要根据训练集，学习出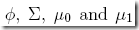

怎么学？最大似然估计

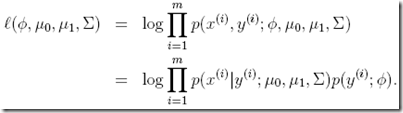
这里和判别学习算法不同，
判别学习算法，对p(y|x; θ)进行建模，所以称为conditional似然估计
而生成学习算法，是对于p(x|y)*p(y)，即p(x,y)进行建模，所以称为joint似然估计

使用最优化算法计算maximizing ℓ，得到参数如下（计算过程略去）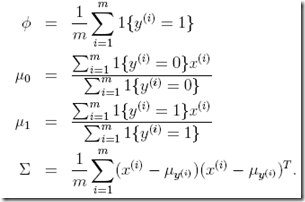

虽然没有写计算过程，但是得到的这个结果是reasonable的
φ就是y=1的概率，算出的结果就是在训练集中y=1的比例
μ0，μ1，结果是训练集中y=0（或y=1）时x的均值，都很合理

计算出这些参数，我们就得到p(x|y = 0)，p(x|y = 1)和p(y)，然后可以使用上面的方法就行预测

Discussion: GDA and logistic regression
这里有个很有趣的结论

We just argued that if p(x|y) is multivariate gaussian (with shared ), then p(y|x) necessarily follows a logistic function. The converse, however, is not true;

当p(x|y)满足multivariate gaussian的时候，p(y|x)一定是logistic function，但反之不成立。
使用视频中的截图，更容易理解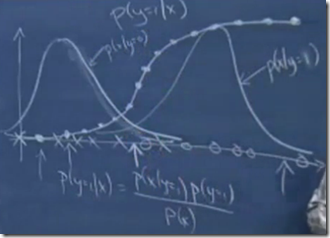

图中，叉表示y=0的点，圈表示y=1的点
所以对于y=0和y=1分别建模，就得到两边的两个bell-shaped的高斯曲线
这时如果要画出p(y=1|x)，就得到中间的sigmod曲线
越靠左y=1的概率越小，越靠右y=1的概率越接近1，在中间两个曲线交界的地方，y=1的概率为0.5
非常形象的说明为什么p(y|x)会是一个logistic function

更酷的是，这个结论可以推广到任何指数族分布，即任何广义线性模型的分布

那么这里产生的问题就是，我们为什么需要GDA，直接使用逻辑回归不可以吗？
两者区别在于，
GDA比逻辑回归做出更强的假设，因为前面的结论是不可逆的
所以当数据p(x|y)确实或近似符合高斯分布时，GDA更有效，并且需要更少的训练数据就可以达到很好的效果
但是在实际中，其实你很难确定这点，
这时逻辑回归有更好的鲁棒性，比如如果p(x|y)符合泊松分布，而你误认为符合高斯分布，而使用GDA，那么效果就会不太好
而逻辑回归，对数据做出的假设比较少，只要p(x|y)指数族分布，都会有比较好的效果，当然逻辑回归需要的训练数据也是比较多的

这里其实就是一个balance
模型假设强弱和训练数据量之间的权衡
如果你明确知道符合高斯分布，那么用比较少的训练数据，使用GDA就很好
如果不确定，就使用逻辑回归，用比较多的训练数据