【bzoj1502】月下柠檬树

Portal -->bzoj1502

Solution

　　额其实说实在这题我一开始卡在了。。这个阴影长啥样上QwQ

　　首先因为是平行光线然后投影到了一个水平面上所以这个投影一定是。。若干个圆再加上这些圆的边界这样组成的

　　额或者说是这样：

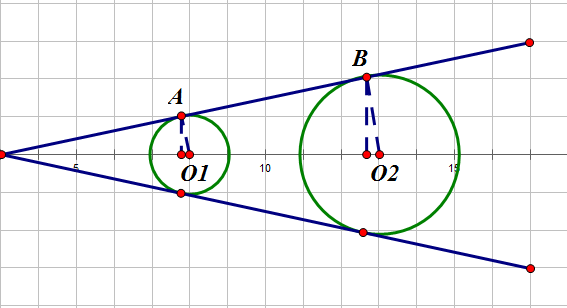
　　就是一些圆和相邻圆的切线组成的边界

　　然后因为这个是。。一段连续的曲线嘛然后的话浮动应该不会太太太太大所以有一种相对简单的方法就是用Simpson积分直接爆搞（虽然说。。如果你特意构造一下数据的话还是可能会被卡掉的qwq）

　　

　　注意到这个图形是对称的所以我们可以先只看一半，然后最后输出的时候乘\(2\)就好了

​　　然后这个边界的话我们可以将它看成一个函数\(f\)，如果要用Simpson积分的话我们需要快速求这个函数在某个点的取值，我们记当前查询\(f(x)\)，那么这个可以分成两种情况：

​　　1、点\((x,f(x))\)在某个圆上，这种时候\(f(x)=\sqrt {r^2-(x-x_O)^2}\)，其中\(x_O\)是这个圆的圆心的横坐标，\(r\)是这个圆的半径

​　　2、点\((x,f(x))\)在某条切线上，那这个时候直接把\(x\)带进这条切线的解析式里面就可以得到\(f(x)\)了

　　然而实际上在实现的时候，并不需要特别分类讨论，只要返回两种算的方法的最大值就好了

　　

　　

　　那么剩下来的问题，就是如何求两个圆的切线

​　　首先我们需要预处理一下，把被包含的圆去掉

　　然后接下来我们只讨论不包含的情况

　　还是用回这张图，我们只看\(x\)轴的上半部分

​　　其中\(A,B\)均为切点，记\(l_{AB}\)与\(x\)轴的夹角为\(\theta\)，\(L=O_1O_2\)，第一个圆的半径为\(r\)，第二个圆的半径为\(R\)

　　由相似我们可以得到\(sin\theta=\frac{R-r}{L}\)，进而我们可以得到\(cos\theta\)

　　然后知道了\(sin\theta\)和\(cos\theta\)之后，我们就可以知道\(A\)和\(B\)的坐标了：

\[\begin{aligned}
A&=(x_{O_1}-sin\theta\cdot r,cos\theta \cdot r)\\
B&=(x_{O_2}-sin\theta\cdot R,cos\theta\cdot R)\\
\end{aligned}
\]

　　然后我们就可以直接求一下\(l_{AB}\)的解析式了，这里不需要担心\(l_{AB}\)的斜率是否存在，因为这个图形保证了不会出现这种情况

　　然后就很愉快滴做完啦ovo

　　

　　代码大概长这个样子（额貌似eps要开到1e-6才不会出锅qwq）：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
const int N=510;
const double eps=1e-6,inf=2147483647;
double h[N],r[N],O[N],k[N],b[N];
double lx[N],rx[N],ly[N],ry[N];
int have[N];
int n,m;
double alpha,L,R;
double val(double x);
double simpson(double l,double r);
void prework();
void calc(int x);
bool in(int x,int y){return fabs(O[x]-O[y])<=fabs(r[x]-r[y]);}
double sqr(double x){return x*x;}
double solve(double l,double r);

int main(){
#ifndef ONLINE_JUDGE
	freopen("a.in","r",stdin);
#endif
	scanf("%d%lf\n",&n,&alpha);
	++n;
	for (int i=1;i<=n;++i){
		scanf("%lf",h+i);
		O[i]=h[i]/tan(alpha)+O[i-1];
	}
	L=inf,R=-inf;
	for (int i=1;i<n;++i) scanf("%lf",r+i);
	for (int i=1;i<=n;++i)
		L=min(O[i]-r[i],L),R=max(O[i]+r[i],R);

	prework();

	printf("%.2lf\n",solve(L,R)*2.0);
}

double solve(double l,double r){
	double mid=(l+r)*0.5,h=simpson(l,r),hmid=simpson(l,mid)+simpson(mid,r);
	if (fabs(r-l)<=eps||(fabs(h-hmid)<=eps)) return hmid;
	return solve(l,mid)+solve(mid,r);
}

double simpson(double l,double r){
	double hl=val(l),hr=val(r),hmid=val((l+r)*0.5);
	return (r-l)*(hl+hr+hmid*4.0)/6.0;
}

double val(double x){
	double ret=0;
	for (int i=1;i<=n;++i)
		if (fabs(x-O[i])<=r[i])
			ret=max(ret,sqrt(sqr(r[i])-sqr(x-O[i])));
	for (int i=1;i<n;++i){
		if (have[i]) continue;
		if (lx[i]<=x&&x<=rx[i])
			ret=max(ret,k[i]*x+b[i]);
	}
	return ret;
}

void prework(){
	for (int i=1;i<n;++i){
		have[i]=in(i,i+1);
		if (have[i]) continue;
		calc(i);
	}
}

void calc(int x){
	double l=(O[x+1]-O[x]);
	double theta=asin((r[x+1]-r[x])/l);
	double x1,y1,x2,y2;
	x1=O[x]-sin(theta)*r[x]; y1=cos(theta)*r[x];
	x2=O[x+1]-sin(theta)*r[x+1]; y2=cos(theta)*r[x+1];
	lx[x]=x1; ly[x]=y1;
	rx[x]=x2; ry[x]=y2;

	k[x]=(y2-y1)/(x2-x1);
	b[x]=y1-k[x]*x1;
}