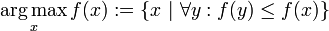符号arg含义
argument of the maximum/minimum
arg max f(x): 当f(x)取最大值时,x的取值
arg min f(x):当f(x)取最小值时,x的取值
表示使目标函数取最小值时的变量值
From Wikipedia
In mathematics, arg max (or argmax) stands for the argument of the maximum, that is to say, the set of points of the given argument for which the value of the given expression attains its maximum value:[note 1]
In other words,
is the set of values of x for which f(x) has the largest value M. For example, if f(x) is 1−|x|, then it attains its maximum value of 1 at x = 0 and only there, so 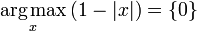 .
.
Equivalently, if M is the maximum of f, then the arg max is the level set of the maximum:
If the maximum is reached at a single value, then one refers to the point as the arg max, meaning we define the arg max as a point, not a set of points. So, for example,
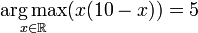 //只有一个值使函数取最大值,则arg为该值
//只有一个值使函数取最大值,则arg为该值
(rather than the singleton set {5}), since the maximum value of x(10 − x) is 25, which happens when x = 5.[note 2]
However, in case the maximum is reached at many values, arg max is a set of points.
Then, we have for example
 //若多个值使函数取最大值,则arg为集合
//若多个值使函数取最大值,则arg为集合
since the maximum value of cos(x) is 1, which happens on this interval when x = 0, 2π or 4π. On the whole real line, the arg max is 
arg min (or argmin) is defined analogously.
Note also that functions do not in general attain a maximum value, and hence will in general not have an arg max: 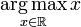 is undefined, as x is unbounded on the real line. However, by the extreme value theorem (or the classical compactness argument), a continuous function on a compact interval has a maximum, and thus an arg max. //若无法取到最大值,无定义
is undefined, as x is unbounded on the real line. However, by the extreme value theorem (or the classical compactness argument), a continuous function on a compact interval has a maximum, and thus an arg max. //若无法取到最大值,无定义
符号arg含义的更多相关文章
- 数学符号arg含义
argument of the maximum/minimum arg max f(x): 当f(x)取最大值时,x的取值 arg min f(x):当f(x)取最小值时,x的取值 表示使目标函数取最 ...
- 压缩感知中的数学知识:稀疏、范数、符号arg min
转自:http://blog.csdn.net/jbb0523/article/details/40262629 1.稀疏:什么是K稀疏呢? 在压缩感知里经常提到 "K稀疏" 的概 ...
- SVN版本控制器中各符号的含义
SVN符号的含义 项目开发过程中,随着学习的不断深入,开始慢慢接触到版本管理控制工具,其实这个工具主要用于团队开发之中,但对于个人项目的备份也有好处,可以避免在电脑出现不可预知的故障时,最大化的保护自 ...
- Linux Shell中的特殊符号和含义简明总结(包含了绝大部份)
case语句适用于需要进行多重分支的应用情况. case分支语句的格式如下: case $变量名 in 模式1) 命令序列1 ;; 模式2) 命令序列2 ;; *) 默认执行的命令序列 ...
- bash 特殊符号的含义
bash常见特殊符号及含义 linux中shell变量的含义解释
- makefile中一些符号的含义
关于gnu make的详细介绍参看http://www.gnu.org/software/make/manual/make.html 规则 让我们先来粗略地看一看Makefile的规则. targ ...
- shell 中的特殊符号的含义
来源:http://blog.sina.com.cn/s/blog_62a151be0100x9rn.html 第四章 基本功 - 特殊符号 学习撰写 script 最迅速的捷径是观摩别人的 scri ...
- linux中的特殊符号及其含义梳理
1. 重定向符号及含义 注意:箭头流向即是数据的流向. 数字0:标准输入(standard input,简写stdin),数据从右往左方向流动 数字1:标准正确输出(standard output,简 ...
- scala中的=>符号的含义
[声明]本帖的内容是copy来的,来源为stack overflow. It has several meanings in Scala, all related to its mathematica ...
随机推荐
- Python max() 方法
描述 Python max() 方法返回字符串中最大的字母(26个字母中最大的是Z). 语法 max() 方法语法: max(S) 参数 S -- 字符串. 返回值 返回字符串中最大的字母. 实例 以 ...
- app hybrid
package com.note.testcases; /** * * The MIT License (MIT) * * Copyright (c) 2016 Alejandro Gómez Mor ...
- mac eclipse 执行adb 命令,提示command not fount
java执行命令: p = Runtime.getRuntime().exec(commandStr); [INFO ] 执行命令结果:nullbash: adb: command not found ...
- mysql 5.6 grant授权的时候出现问题
mysql> grant select on huamu_licai.* to 'read'@'%' identified by password 'Abcd1234';ERROR 1827 ( ...
- iOS学习笔记(八)——iOS网络通信http之NSURLConnection
转自:http://blog.csdn.net/xyz_lmn/article/details/8968182 移动互联网时代,网络通信已是手机终端必不可少的功能.我们的应用中也必不可少的使用了网络通 ...
- BestCoder Round #4 Miaomiao's Geometry (暴力)
Problem Description There are N point on X-axis . Miaomiao would like to cover them ALL by using seg ...
- Azure Redis
https://azure.microsoft.com/en-us/blog/mvc-movie-app-with-azure-redis-cache-in-15-minutes/ https://a ...
- maven(4)------maven核心pom.xml文件常用元素分析
在maven项目中,pom文件是核心文件 pom.xml: <?xml version="1.0" encoding="UTF-8"?> <p ...
- dubbo的一些默认变量
dubbo默认变量表 变量名 描述 默认值 用途 DEFAULT_IO_THREADS 默认IO线程 Math.min(Runtime.getRuntime().availableProcessors ...
- VC++ 知识点
1.寻找文件时,CFileFind类的使用. 2.寻找目录时使用BROWSEINFO,其中包含了用户选中目录的重要信息. 3.LPITEMIDLIST类 4.目录选择对话框的使用SHBrowseFor ...