2012Noip提高组Day1 T3 开车旅行

题目描述

小 A 和小 B 决定利用假期外出旅行，他们将想去的城市从 1 到 N 编号，且编号较小的

城市在编号较大的城市的西边，已知各个城市的海拔高度互不相同，记城市 i 的海拔高度为

Hi，城市 i 和城市 j 之间的距离 d[i,j]恰好是这两个城市海拔高度之差的绝对值，即

d[i,j] = |Hi− Hj|。

旅行过程中，小 A 和小 B 轮流开车，第一天小 A 开车，之后每天轮换一次。他们计划

选择一个城市 S 作为起点，一直向东行驶，并且最多行驶 X 公里就结束旅行。小 A 和小 B

的驾驶风格不同，小 B 总是沿着前进方向选择一个最近的城市作为目的地，而小 A 总是沿

着前进方向选择第二近的城市作为目的地（注意：本题中如果当前城市到两个城市的距离

相同，则认为离海拔低的那个城市更近）。如果其中任何一人无法按照自己的原则选择目的

城市，或者到达目的地会使行驶的总距离超出 X 公里，他们就会结束旅行。

在启程之前，小 A 想知道两个问题：

1．对于一个给定的 X=X0，从哪一个城市出发，小 A 开车行驶的路程总数与小 B 行驶

的路程总数的比值最小（如果小 B 的行驶路程为 0，此时的比值可视为无穷大，且两个无穷大视为相等）。如果从多个城市出发，小 A 开车行驶的路程总数与小 B 行驶的路程总数的比

值都最小，则输出海拔最高的那个城市。

1. 对任意给定的 X=Xi和出发城市 Si，小 A 开车行驶的路程总数以及小 B 行驶的路程

总数。

输入输出格式

输入格式：

第一行包含一个整数 N，表示城市的数目。

第二行有 N 个整数，每两个整数之间用一个空格隔开，依次表示城市 1 到城市 N 的海

拔高度，即 H1，H2，……，Hn，且每个 Hi都是不同的。

第三行包含一个整数 X0。

第四行为一个整数 M，表示给定 M 组 Si和 Xi。

接下来的 M 行，每行包含 2 个整数 Si和 Xi，表示从城市 Si出发，最多行驶 Xi公里。

输出格式：

输出共 M+1 行。

第一行包含一个整数 S0，表示对于给定的 X0，从编号为 S0的城市出发，小 A 开车行驶

的路程总数与小 B 行驶的路程总数的比值最小。

接下来的 M 行，每行包含 2 个整数，之间用一个空格隔开，依次表示在给定的 Si和

Xi下小 A 行驶的里程总数和小 B 行驶的里程总数。

输入输出样例

输入样例#1：

drive1
4
2 3 1 4
3
4
1 3
2 3
3 3
4 3

drive2
 10
4 5 6 1 2 3 7 8 9 10
7
10
1 7
2 7
3 7
4 7
5 7
6 7
7 7
8 7
9 7
10 7

输出样例#1：

drive1
1
1 1
2 0
0 0
0 0 

drive2
2
3 2
2 4
2 1
2 4
5 1
5 1
2 1
2 0
0 0
0 0

说明

【输入输出样例 1 说明】

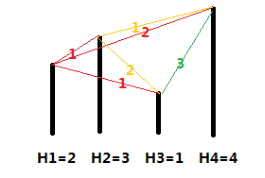
各个城市的海拔高度以及两个城市间的距离如上图所示。

如果从城市 1 出发，可以到达的城市为 2,3,4，这几个城市与城市 1 的距离分别为 1,1,2，

但是由于城市 3 的海拔高度低于城市 2，所以我们认为城市 3 离城市 1 最近，城市 2 离城市

1 第二近，所以小 A 会走到城市 2。到达城市 2 后，前面可以到达的城市为 3,4，这两个城

市与城市 2 的距离分别为 2,1，所以城市 4 离城市 2 最近，因此小 B 会走到城市 4。到达城

市 4 后，前面已没有可到达的城市，所以旅行结束。

如果从城市 2 出发，可以到达的城市为 3,4，这两个城市与城市 2 的距离分别为 2,1，由

于城市 3 离城市 2 第二近，所以小 A 会走到城市 3。到达城市 3 后，前面尚未旅行的城市为

4，所以城市 4 离城市 3 最近，但是如果要到达城市 4，则总路程为 2+3=5>3，所以小 B 会

直接在城市 3 结束旅行。

如果从城市 3 出发，可以到达的城市为 4，由于没有离城市 3 第二近的城市，因此旅行

还未开始就结束了。

如果从城市 4 出发，没有可以到达的城市，因此旅行还未开始就结束了。

【输入输出样例 2 说明】

当 X=7 时，

如果从城市 1 出发，则路线为 1 -> 2 -> 3 -> 8 -> 9，小 A 走的距离为 1+2=3，小 B 走的

距离为 1+1=2。（在城市 1 时，距离小 A 最近的城市是 2 和 6，但是城市 2 的海拔更高，视

为与城市 1 第二近的城市，所以小 A 最终选择城市 2；走到 9 后，小 A 只有城市 10 可以走，

没有第 2 选择可以选，所以没法做出选择，结束旅行）

如果从城市 2 出发，则路线为 2 -> 6 -> 7 ，小 A 和小 B 走的距离分别为 2，4。

如果从城市 3 出发，则路线为 3 -> 8 -> 9，小 A 和小 B 走的距离分别为 2，1。

如果从城市 4 出发，则路线为 4 -> 6 -> 7，小 A 和小 B 走的距离分别为 2，4。

如果从城市 5 出发，则路线为 5 -> 7 -> 8 ，小 A 和小 B 走的距离分别为 5，1。

如果从城市 6 出发，则路线为 6 -> 8 -> 9，小 A 和小 B 走的距离分别为 5，1。

如果从城市 7 出发，则路线为 7 -> 9 -> 10，小 A 和小 B 走的距离分别为 2，1。

如果从城市 8 出发，则路线为 8 -> 10，小 A 和小 B 走的距离分别为 2，0。

如果从城市 9 出发，则路线为 9，小 A 和小 B 走的距离分别为 0，0（旅行一开始就结

束了）。

如果从城市 10 出发，则路线为 10，小 A 和小 B 走的距离分别为 0，0。

从城市 2 或者城市 4 出发小 A 行驶的路程总数与小 B 行驶的路程总数的比值都最小，

但是城市 2 的海拔更高，所以输出第一行为 2。

【数据范围】

对于 30%的数据，有 1≤N≤20，1≤M≤20；

对于 40%的数据，有 1≤N≤100，1≤M≤100；

对于 50%的数据，有 1≤N≤100，1≤M≤1,000；

对于 70%的数据，有 1≤N≤1,000，1≤M≤10,000；

对于100%的数据，有1≤N≤100,000，1≤M≤10,000，-1,000,000,000≤Hi≤1,000,000,000，

0≤X0≤1,000,000,000，1≤Si≤N，0≤Xi≤1,000,000,000，数据保证 Hi互不相同。

很显然我们需要一个比n^2暴力找最近第二近城市的更优的算法。

我们可以用链表，把城市按高度从低到高排序，然后相邻的城市连起来，然后我们从原来城市编号里，从第一个城市开始寻找，很明显对于原来标号为i的城市，在排序后里面，它的最近和第二近的城市就是它排序后所在位置向左两个(i-1,i-2)到向右两个(i+1,i+2)这四个城市中的两个，找完之后这个城市i就可以删掉了（因为开车要一路向东，编号是递增的，所以可以删掉已经找完的），然后再把i-1和i+1连起来就可以了。

之后我们还可以发现其实对于一个起点来说，它怎么走是已经确定了的，相比我们一步一步模拟地走，我们可以采取倍增的方法，多步多步地走就可以更优了。

我们可以把A，B各行动一次作为一次行动，然后最后再判一次A能不能再走一次就可以了。

 #include <cstring>
 #include <cstdio>
 #include <iostream>
 #include <algorithm>
 #define N 100005
 using namespace std;
 struct data{
     int hi,sign;
 }city[N];
 int n,m,x,y,num,x0,f[N][],pre[N],next[N],fir[N],sec[N],head[N];
 double qwq,ans;
 long long a[N][],b[N][];
 bool cmp(const struct data a,const struct data b){
     return (a.hi<b.hi);
 }
 void solve(int x){
     fir[x]=(pre[x]&&(city[x].hi-city[pre[x]].hi<=city[next[x]].hi-city[x].hi||!next[x]))?pre[x]:next[x];
     if (fir[x]==pre[x])
         sec[x]=(pre[pre[x]]&&(city[x].hi-city[pre[pre[x]]].hi<=city[next[x]].hi-city[x].hi||!next[x]))?pre[pre[x]]:next[x];
     else sec[x]=(pre[x]&&(city[x].hi-city[pre[x]].hi<=city[next[next[x]]].hi-city[x].hi||!next[next[x]]))?pre[x]:next[next[x]];
     pre[next[x]]=pre[x];
     next[pre[x]]=next[x];
 }
 void work(int u,int x0){
     for (int i=;i>=;i--)
         if ((f[u][i])&&(x0-a[u][i]-b[u][i]>=)){
             x+=a[u][i];
             y+=b[u][i];
             x0=x0-a[u][i]-b[u][i];
             u=f[u][i];
         }
     if ((x0-a[u][]>=)&&(sec[u])){
         x+=a[u][];
         u=sec[u];
     }
 }
 int main(){
     scanf("%d",&n);
     for (int i=;i<=n;++i){
         scanf("%d",&city[i].hi);
         city[i].sign=i;
     }
     sort(city+,city++n,cmp);
     for (int i=;i<=n;++i){
         head[city[i].sign]=i;
         pre[i]=i-;
         next[i]=i+;
         if (i==n) next[i]=;
     }
     for (int i=;i<=n;i++)
      solve(head[i]);
     for (int i=;i<=n;++i){
         f[i][]=fir[sec[i]];
         a[i][]=abs(city[i].hi-city[sec[i]].hi);
         b[i][]=abs(city[sec[i]].hi-city[fir[sec[i]]].hi);
     }
     for (int j=;j<=;++j)
      for (int i=;i<=n;++i){
         f[i][j]=f[f[i][j-]][j-];
         a[i][j]=a[i][j-]+a[f[i][j-]][j-];
         b[i][j]=b[i][j-]+b[f[i][j-]][j-];
     }
     scanf("%d",&x0);
     ans=<<;num=;
     for (int i=;i<=n;++i){
         x=y=qwq=;
         work(head[i],x0);
         if (y==) qwq=<<-;
         else qwq=(double)x/(double)y;
         if ((ans>qwq)||(ans==qwq&&city[head[num]].hi<city[i].hi)){
             ans=qwq;
             num=i;
         }
     }
     printf("%d\n",num);
     scanf("%d",&m);
     int qaq;
     while (m--){
         x=y=;
         scanf("%d%d",&qaq,&x0);
         work(head[qaq],x0);
         printf("%d %d\n",x,y);
     }
     return ;
 }

开车旅行

n^2暴力预处理最近第二近的然后暴力跑跑什么的也有50、70分也好良心啊.......