K：二叉查找树(BST)
相关介绍:
二叉查找树（英语：Binary Search Tree），也称二叉搜索树、有序二叉树（英语：ordered binary tree），排序二叉树（英语：sorted binary tree），二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。
二叉查找树的定义：
二叉查找树或者是一棵空树，或者是一棵具有以下性质的二叉树:
当左子树不为空，则左子树上所有节点的值均小于根节点的值
当右子树不为空，则右子树上所有节点的值均大于根节点的值
它的左右子树也都是二叉查找树
下图显示的二叉树便是一棵二叉查找树：
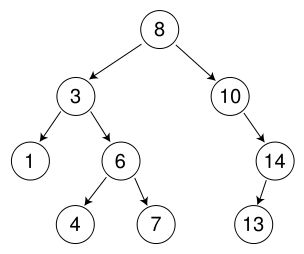
有趣的是，对二叉查找树进行中序遍历，得到的结果，其是一个按照关键字有序的记录序列
二叉查找树的相关知识点：
对于二叉查找树，其主要的方法是查找、插入、删除相关的节点，以下介绍其相关的操作过程及给出相应的代码，在给出相关的操作之前，给出相关节点类的代码描述
二叉查找树的节点类：
/**
* 二叉查找树的相关节点类
* @author 学徒
*
*/
class BinarySearchTreeNode
{
//节点的左子树指针
BinarySearchTreeNode left;
//节点的右子树指针
BinarySearchTreeNode right;
//关键字值
Comparable key;
//该节点的相关数据
Object data;
public BinarySearchTreeNode(BinarySearchTreeNode left,BinarySearchTreeNode right,Comparable key,Object data)
{
this.left=left;
this.right=right;
this.key=key;
this.data=data;
}
public BinarySearchTreeNode(Comparable key,Object data)
{
this(null,null,key,data);
}
}
二叉查找树的查找过程：
若将查找表组织为一棵二叉查找树，则根据二叉查找树的特点，查找过程的主要步骤归纳如下：
- 若查找树为空，则查找失败
- 若查找树非空，则
- 若给定值k等于根节点的关键字值，则查找成功，结束查找过程，否则转步骤2
- 若给定值k小于根节点的关键字值，则继续在根节点的左子树上进行，否则转3
- 若给定值k大于根节点的关键字值，则继续在根节点的右子树上进行
相关代码：
/**
* 二叉查找树的查找操作
* @param data 需要进行查找的相关数据
* @return 查找到的相关的结果，当查找失败时，返回null
*/
public Object search(Comparable key)
{
if(key==null)
{
return null;
}
return toSearch(root,key);
}
/**
* 在二叉查找树中进行递归的查找的方法
* @param data 需要进行查找的数据
* @param node 二叉树中某个子树的根节点
* @return 查找的节点类的结果
*/
private Object toSearch(BinarySearchTreeNode node,Comparable key)
{
if(node==null)
{
return null;
}
//与根节点的相关值进行比较并选择合适的分支
int compara=node.key.compareTo(key);
if(compara==0)
return node.data;
else if(compara<0)
return toSearch(node.right,key);
else
return toSearch(node.left,key);
}
二叉查找树的插入操作：
二叉查找树中，插入一个新节点的过程为，假设待插入节点的关键字值为key，为了将其插入到表中，先要将它放入二叉排序树中进行查找，若查找成功，则按二叉查找树的定义，待插入节点已经存在，不必插入；否则，将新节点插入到表中。因此，新插入的节点一定是作为叶子节点添加到表中去的。其相关示例代码如下：
相关代码：
/**
* 用于往二叉树中插入一个新的节点
* @param key 该节点的关键字
* @param data 该节点的相关数据
* @return 插入的结果，返回false有两种情况，一种是节点本身已存在，一种是需要插入的节点的关键字值为null
*/
public boolean insert(Comparable key,Object data)
{
if(key==null)
return false;
if(root==null)
{
root=new BinarySearchTreeNode(key,data);
return true;
}
else
return insertNode(root,key,data);
}
/**
* 往二叉查找树中插入相关的节点
* @param key 节点的关键字值
* @param data 节点的相关数据
* @param node 需要进行插入的子树的根节点
* @return 插入的结果
*/
public boolean insertNode(BinarySearchTreeNode node,Comparable key,Object data)
{
int compare=key.compareTo(node.key);
//已存在节点时，返回false
if(compare==0)
return false;
//要进行插入的节点比根节点的关键字值小的时候
else if(compare<0)
{
//左子树为空则插入左子树
if(node.left==null)
{
node.left=new BinarySearchTreeNode(key,data);
return true;
}
//非空则继续递归的查找
else
return insertNode(node.left,key,data);
}
else
{
if(node.right==null)
{
node.right=new BinarySearchTreeNode(key,data);
return true;
}
else
return insertNode(node.right,key,data);
}
}
二叉树的删除操作：
与在二叉树上进行插入操作的要求相同，从二叉查找树中删除一个节点，要保证删除后仍然是一棵二叉查找树。根据二叉查找树的结构特征，删除操作可分为4种情况来考虑：
若待删除的节点是叶子节点，则直接删除该节点即可。若该节点同时也是根节点，则删除后二叉查找树变为空树
若待删除的节点只有左子树，没有右子树，则根据二叉排序树的特点，可以直接将其左子树的根节点替代被删除节点的位置，即若被删除的节点为其双亲节点的左孩子，则将被删除节点的唯一左孩子收为其双亲节点的左孩子；否则收其为双亲节点的右孩子
待删除的节点只有右子树，而无左子树。则可以直接将其右子树的根节点替代被删除节点的位置，即若被删除的节点为其双亲节点的左孩子，则将被删除节点的唯一右孩子收其为双亲节点的左孩子；否则收为其双亲节点的右孩子
待删除节点既有左子树，又有右子树。根据二叉查找树的特点，可以用被删除节点的中序遍历序列下的前驱节点(或者中序遍历序列下的后继节点)替代被删除节点，同时删除其中序遍历序列下的前驱节点(或中序遍历序列下的后继节点)。而被删除节点(指的是新的删除节点)在中序遍历下的前驱无右子树(被删除节点在中序遍历下的无后继左子树)因而问题转化为情况2或者情况3
以下代码中，当其删除节点的左右子树均存在的时候，考虑的是选择其中序遍历序列下的后继节点替代被删除节点
相关代码：
/**
* 用于删除操作
* @param key 删除的节点的关键字
* @return 返回所删除节点所对应的数据，当不存在关键字时返回null
*/
public Object delete(Comparable key)
{
if(key==null)
return null;
else
return remove(root,key,null);
}
/**
* 用于删除操作所调用的一个方法，在以node为根的二叉查找树中删除关键字值为key的节点，parent为node的父节点，采用递归的方式
* @param node 以此节点为根的二叉树
* @param key 需要进行删除节点的关键字
* @param parent 以node节点为根的二叉树的node节点的父节点
* @return 所删除节点的数据
*/
public Object remove(BinarySearchTreeNode node,Comparable key,BinarySearchTreeNode parent)
{
if(node!=null)
{
int compare =key.compareTo(node.key);
//从左子树中进行删除
if(compare<0)
{
return remove(node.left,key,node);
}
//从右子树中进行删除
else if(compare>0)
{
return remove(node.right,key,node);
}
//当前节点即为要进行删除的节点
else
{
//当前要进行删除的节点的数据
Object result=node.data;
//当前要进行删除的节点的左右子树均存在
if(node.left!=null&&node.right!=null)
{
//寻找要进行删除节点的替换节点
BinarySearchTreeNode innext=node.right;
//进行进行替换的节点的父节点
BinarySearchTreeNode innextParent=node;
//寻找右子树下的最左孩子节点
while(innext.left!=null)
{
innextParent=innext;
innext=innext.left;
}
//改变删除节点的相关数据
node.data=innext.data;
node.key=innext.key;
//递归的从二叉查找树中删除要进行替换的节点
remove(node.right,innext.key,node);
}
//以下考虑的情况均当前删除节点缺少左子树或者右子树的情况
else
{
//当前要进行删除的节点不为根节点的时候
if(parent!=null)
{
//当左子树不为空的时候
if(node.left!=null&&node.right==null)
{
//当前节点为其左子树节点的时候
if(node==parent.left)
{
parent.left=node.left;
}
//当前节点为其右子树节点的时候
else
{
parent.right=node.left;
}
}
//当右子树不为空的时候
else if(node.left==null&&node.right!=null)
{
//当前节点为其左子树节点的时候
if(node==parent.left)
{
parent.left=node.right;
}
//当前节点为其右子树节点的时候
else
{
parent.right=node.right;
}
}
}
//当前删除的节点为根节点的时候
else
{
if(node.left!=null)
root=node.left;
else
root=node.right;
}
}
//返回其进行删除的节点的值
return result;
}
}
return null;
}
其完整代码如下：
package all_in_tree;
/**
* 该类用于演示二叉查找树相关的操作
* @author 学徒
*
*/
public class BinarySearchTree
{
//用于指向一棵二叉查找树的根节点的指针
private BinarySearchTreeNode root;
/**
* 二叉查找树的查找操作
* @param data 需要进行查找的相关数据
* @return 查找到的相关的结果，当查找失败时，返回null
*/
public Object search(Comparable key)
{
if(key==null)
{
return null;
}
return toSearch(root,key);
}
/**
* 在二叉查找树中进行递归的查找的方法
* @param data 需要进行查找的数据
* @param node 二叉树中某个子树的根节点
* @return 查找的节点类的结果
*/
private Object toSearch(BinarySearchTreeNode node,Comparable key)
{
if(node==null)
{
return null;
}
//与根节点的相关值进行比较并选择合适的分支
int compara=node.key.compareTo(key);
if(compara==0)
return node.data;
else if(compara<0)
return toSearch(node.right,key);
else
return toSearch(node.left,key);
}
/**
* 用于往二叉树中插入一个新的节点
* @param key 该节点的关键字
* @param data 该节点的相关数据
* @return 插入的结果，返回false有两种情况，一种是节点本身已存在，一种是需要插入的节点的关键字值为null
*/
public boolean insert(Comparable key,Object data)
{
if(key==null)
return false;
if(root==null)
{
root=new BinarySearchTreeNode(key,data);
return true;
}
else
return insertNode(root,key,data);
}
/**
* 往二叉查找树中插入相关的节点
* @param key 节点的关键字值
* @param data 节点的相关数据
* @param node 需要进行插入的子树的根节点
* @return 插入的结果
*/
public boolean insertNode(BinarySearchTreeNode node,Comparable key,Object data)
{
int compare=key.compareTo(node.key);
//已存在节点时，返回false
if(compare==0)
return false;
//要进行插入的节点比根节点的关键字值小的时候
else if(compare<0)
{
//左子树为空则插入左子树
if(node.left==null)
{
node.left=new BinarySearchTreeNode(key,data);
return true;
}
//非空则继续递归的查找
else
return insertNode(node.left,key,data);
}
else
{
if(node.right==null)
{
node.right=new BinarySearchTreeNode(key,data);
return true;
}
else
return insertNode(node.right,key,data);
}
}
/**
* 用于删除操作
* @param key 删除的节点的关键字
* @return 返回所删除节点所对应的数据，当不存在关键字时返回null
*/
public Object delete(Comparable key)
{
if(key==null)
return null;
else
return remove(root,key,null);
}
/**
* 用于删除操作所调用的一个方法，在以node为根的二叉查找树中删除关键字值为key的节点，parent为node的父节点，采用递归的方式
* @param node 以此节点为根的二叉树
* @param key 需要进行删除节点的关键字
* @param parent 以node节点为根的二叉树的node节点的父节点
* @return 所删除节点的数据
*/
public Object remove(BinarySearchTreeNode node,Comparable key,BinarySearchTreeNode parent)
{
if(node!=null)
{
int compare =key.compareTo(node.key);
//从左子树中进行删除
if(compare<0)
{
return remove(node.left,key,node);
}
//从右子树中进行删除
else if(compare>0)
{
return remove(node.right,key,node);
}
//当前节点即为要进行删除的节点
else
{
//当前要进行删除的节点的数据
Object result=node.data;
//当前要进行删除的节点的左右子树均存在
if(node.left!=null&&node.right!=null)
{
//寻找要进行删除节点的替换节点
BinarySearchTreeNode innext=node.right;
//进行进行替换的节点的父节点
BinarySearchTreeNode innextParent=node;
//寻找右子树下的最左孩子节点
while(innext.left!=null)
{
innextParent=innext;
innext=innext.left;
}
//从二叉查找树中删除该要进行替换的节点即节点innext
innextParent.left=null;
//改变删除节点的相关数据
node.data=innext.data;
node.key=innext.key;
}
//以下考虑的情况均当前删除节点缺少左子树或者右子树的情况
else
{
//当前要进行删除的节点不为根节点的时候
if(parent!=null)
{
//当左子树不为空的时候
if(node.left!=null&&node.right==null)
{
//当前节点为其左子树节点的时候
if(node==parent.left)
{
parent.left=node.left;
}
//当前节点为其右子树节点的时候
else
{
parent.right=node.left;
}
}
//当右子树不为空或者删除节点为叶子节点的时候
else
{
//当前节点为其左子树节点的时候
if(node==parent.left)
{
parent.left=node.right;
}
//当前节点为其右子树节点的时候
else
{
parent.right=node.right;
}
}
}
//当前删除的节点为根节点的时候
else
{
if(node.left!=null)
root=node.left;
else
root=node.right;
}
}
//返回其进行删除的节点的值
return result;
}
}
return null;
}
}
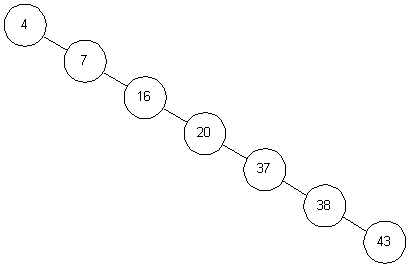
分析：对于二叉查找树，其树结构是在插入和删除节点中动态进行生成的，为此，其查找树的深度依赖于插入节点的顺序。为此，其可能出现如下图所示的一种情况。当插入节点的顺序为有序的时候(节点关键字为有序的)其可能会出现严重“偏拐”的现象而导致其插入和删除的效率均变为O（n）。而平衡二叉树的提出便是为了解决这个问题。详情请点击查看相关博文K：平衡二叉树(AVL)
K：二叉查找树(BST)的更多相关文章
- 【查找结构 2】二叉查找树 [BST]
当所有的静态查找结构添加和删除一个数据的时候,整个结构都需要重建.这对于常常需要在查找过程中动态改变数据而言,是灾难性的.因此人们就必须去寻找高效的动态查找结构,我们在这讨论一个非常常用的动态查找树— ...
- 查找系列合集-二叉查找树BST
一. 二叉树 1. 什么是二叉树? 在计算机科学中,二叉树是每个结点最多有两个子树的树结构. 通常子树被称作“左子树”(left subtree)和“右子树”(right subtree). 二叉树常 ...
- 二叉查找树BST 模板
二叉查找树BST 就是二叉搜索树 二叉排序树. 就是满足 左儿子<父节点<右儿子 的一颗树,插入和查询复杂度最好情况都是logN的,写起来很简单. 根据BST的性质可以很好的解决这些东 ...
- 二叉查找树(BST)
二叉查找树(BST):使用中序遍历可以得到一个有序的序列
- [学习笔记] 二叉查找树/BST
平衡树前传之BST 二叉查找树(\(BST\)),是一个类似于堆的数据结构, 并且,它也是平衡树的基础. 因此,让我们来了解一下二叉查找树吧. (其实本篇是作为放在平衡树前的前置知识的,但为了避免重复 ...
- 二叉查找树(BST)的实现
一.二叉树介绍 二叉查找树(Binary Search Tree,BST),又称二叉排序树,也称二叉搜索树,它或者是一颗空树,或者具有如下性质的树:若它的左子树不为空,则左子树上所有节点的值都小于根节 ...
- 3.2 符号表之二叉查找树BST
一.插入和查找 1.二叉查找树(Binary Search Tree)是一棵二叉树,并且每个结点都含有一个Comparable的键,保证每个结点的键都大于其左子树中任意结点的键而小于其右子树的任意结点 ...
- 从一段简单算法题来谈二叉查找树(BST)的基础算法
先给出一道很简单,喜闻乐见的二叉树算法题: 给出一个二叉查找树和一个目标值,如果其中有两个元素的和等于目标值则返回真,否则返回假. 例如: Input: 5 / \ 3 6 / \ \ 2 4 7 T ...
- 二叉查找树BST
每棵子树头节点的值都比各自左子树上所有节点值要大,也都比各自右子树上所有节点值要小. 二叉查找树的中序遍历序列一定是从小到大排列的. 一个节点的后继节点是指,这个节点在中序遍历序列中的下一个节点.相应 ...
随机推荐
- jvm学习笔记（一）
一.java的运行原理 开发人员编写java代码(.java文件) 编译器将.java文件编译成字节码文件(.class文件) 字节码被装入内存,当字节码被装入内存之后,它就会被解释器解释执行或是被即 ...
- Leetcode 102 二叉树的层次遍历 Python
二叉树的层次遍历 给定一个二叉树,返回其按层次遍历的节点值. (即逐层地,从左到右访问所有节点). 例如: 给定二叉树: [3,9,20,null,null,15,7], 3 / \ 9 20 ...
- Flink学习笔记-新一代Flink计算引擎
说明:本文为<Flink大数据项目实战>学习笔记,想通过视频系统学习Flink这个最火爆的大数据计算框架的同学,推荐学习课程: Flink大数据项目实战:http://t.cn/EJtKh ...
- django 运行报错汇总
记录自己在使用django开发过程中遇到的问题,不间断更新. (1) 独立运行普通Python脚本调用django中定义的类报错 报错信息: django.core.exceptions.Improp ...
- php 逐行读取文本文件
在读取文本时,我们要注意一个事情,那就是换行符,应为我们在写文档时会手动换行,这个换行符需不需要保存就要看自己的需求了. 这里封装了两个方法,一个保留换行,一个不保留.$path为文件路径+文件名 1 ...
- 简单创建一个完整的struts2框架小程序
要完成一个struts2框架的搭建, 1.首先应该从官网上下载最新的jar包,网络连接:http://struts.apache.org/download.cgi#struts2514.1,选择下载F ...
- 设计简单登录界面（Java web）
程序设计思想: 在Input.jsp中创建一个表格里边分别是课程名称,任课老师,教学地点,并分别用三个文本框来接受输入的三个属性, 并传到另外的Jsp页面中,又来接受三个数据,并判断传来的教师,与教室 ...
- 【Quartz】工作原理
本文参考至http://www.cnblogs.com/davidwang456/p/4205237.html和https://blog.csdn.net/guolong1983811/article ...
- Spark构成
RDD Spark基本的数据结构叫弹性分布式数据集(Resilient Distributed Datasets,简称RDD). 概念: 一个分布于集群节点的只读数据集合,并以容错的.并行的方式进行维 ...
- User类 新增共有属性Current ID
一.题目描述 每个用户有用户编号(id),用户名(name),密码(passwd)三个属性.其中: 用户编号(id)由系统自动顺序编号,用户名和密码都是字母.数字.符合的组合,新用户密码,默认“111 ...