DNA Sequence POJ - 2778 （ac自动机 + 快速幂）

题意：

　　给出患病的DNA序列，问序列长度为n的，且不包含患病的DNA序列有多少种

解析：

　　以给出的患病DNA序列建trie树  患病结点要用flag标记

对于长度为n的序列 位置i有四种 情况A  C  T  G， buid的时候是从祖结点0开始的四种选择，如果tri树中存在某种选择，则顺着走下去，因为要防止恰好选择了患病DNA序列

若trie树中不存在某种选择，则指向0 即祖结点，因为这个点中断了患病DNA序列的生成

偷个图：https://blog.csdn.net/morgan_xww/article/details/7834801

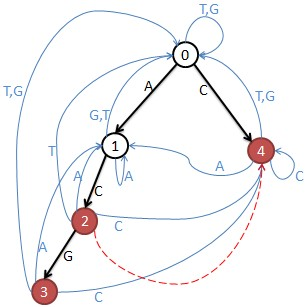
危险结点要去掉，结点3和4是单词结尾所以危险，结点2的fail指针指向4，当匹配”AC”时也就匹配了”C”，所以2也是危险的。

解释一下为什么要去掉单词结尾

因为选择单词 结尾时必定是顺着树走下来的  比如说 如果选择了3  必定上一个是2  上上个是1

比如这次选择了3 而上一个是1  这种是不存在的  因为选了1后 这次想选3  而1在trie中 没有一步通向3的路  所以指向0结点 从0结点选

就是如果一个选择中断了患病DNA序列的生成  指向0就好了

矩阵i行j列的权值是结点i转移到结点j的方案数

而进行k次转移，从结点i转移到结点j的方案数是这个矩阵的k次幂

为什么？

首先解决这个问题：给定一个有向图，问从A点恰好走k步（允许重复经过边）到达B点的方案数mod p的值

把给定的图转为邻接矩阵，即A(i,j)=1当且仅当存在一条边i->j。令C=A*A，那么C(i,j)=ΣA(i,k)*A(k,j)，实际上就等于从点i到点j恰好经过2条边的路径数（枚举k为中转点）。类似地，C*A的第i行第j列就表示从i到j经过3条边的路径数。同理，如果要求经过k步的路径数，我们只需要二分求出A^k即可。

所以最后累加

    LL ret = ;
    for(int i=; i<=tot; i++)
    {
        ret = (ret + A.v[][i]) % MOD;
    }

枚举最后的节点是哪一个  因为起始节点肯定为0，而终止结点可以为0-tot的任何一个，所以累加从0到所有结点的方案数，即包含了所有情况

吐槽。。emm。。为什么函数的矩阵快速幂板子 结果是错了。。。。

#include <iostream>
#include <cstdio>
#include <sstream>
#include <cstring>
#include <map>
#include <set>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
#include <cmath>
#define rap(i, a, n) for(int i=a; i<=n; i++)
#define rep(i, a, n) for(int i=a; i<n; i++)
#define lap(i, a, n) for(int i=n; i>=a; i--)
#define lep(i, a, n) for(int i=n; i>a; i--)
#define MOD 100000
#define LL long long
#define ULL unsigned long long
#define Pair pair<int, int>
#define mem(a, b) memset(a, b, sizeof(a))
#define _  ios_base::sync_with_stdio(0),cin.tie(0)
//freopen("1.txt", "r", stdin);
using namespace std;
const int maxn = , maxm = , INF = 0x7fffffff;
int idx[];
int tot;
queue<int> q;

struct Matrix
{
    __int64 v[][];
    Matrix()
    {
        memset(v, , sizeof(v));
    }
    Matrix operator *(const Matrix B)    // 重载的速度比写独立的函数慢点。
    {
        int i, j, k;
        Matrix C;
        for(i = ; i <= tot; i ++)
            for(j = ; j <= tot; j ++)
                for(k = ; k <= tot; k ++)
                {
                    C.v[i][j] = (C.v[i][j] + v[i][k] * B.v[k][j]) % MOD;
                }
        return C;
    }
};

struct state
{
    int next[];
    int fail, flag;
}trie[];

void init()
{
    while(!q.empty()) q.pop();
    for(int i=; i<maxm; i++)
    {
        mem(trie[i].next, );
        trie[i].fail = trie[i].flag = ;
    }
    tot = ;
}

void insert(char *s)
{
    int  n = strlen(s);
    int rt = ;
    for(int i=;i<n; i++)
    {
        int x = idx[s[i]];
        if(!trie[rt].next[x])
        {
            trie[rt].next[x] = ++tot;
       //     cout<< tot <<endl;
        }
        rt = trie[rt].next[x];
    }
    trie[rt].flag = ;
}

void build()
{
    trie[].fail= -;
    q.push();
    while(!q.empty())
    {
        int u = q.front(); q.pop();
        for(int i=; i<; i++)
        {
            if(trie[u].next[i] == )
            {
                if(u == ) trie[u].next[i] = ;
                else trie[u].next[i] = trie[trie[u].fail].next[i];
            }
            else
            {
                if(u == ) trie[trie[u].next[i]].fail  = ;
                else{
                    int v = trie[u].fail;
                    while(v != -)
                    {
                        if(trie[v].next[i])
                        {
                            trie[trie[u].next[i]].fail = trie[v].next[i];
                            trie[trie[u].next[i]].flag |= trie[trie[v].next[i]].flag;
                            break;
                        }
                        v = trie[v].fail;
                    }
                    if(v == -) trie[trie[u].next[i]].fail = ;
                }
                q.push(trie[u].next[i]);
            }
        }
    }
}

Matrix mtPow(Matrix A, int k)           // 用位运算代替递归求 A^k。
{
    int i;
    Matrix B;
    for(i = ; i <= tot; i ++)
    {
        B.v[i][i] = ;
    }
    while(k)
    {
        if(k & ) B = B * A;
        A = A * A;
        k >>= ;
    }
    return B;
}

int m, n;
char s[];
int main()
{
    init();
    idx['A']=; idx['C']=; idx['T']=; idx['G']=;
    scanf("%d%d", &m, &n);
    rap(i, , m)
    {
        scanf("%s", s);
        insert(s);
     //   cout<< 111 <<endl;
    }
    build();
    Matrix A;
   // for(int i=0; i<=tot; i++) mat[i][i] = 1;
    for(int i=; i<=tot; i++)
    {
        if(trie[i].flag) continue;
        for(int j=; j<; j++)
        {
            if(trie[trie[i].next[j]].flag) continue;
            ++A.v[i][trie[i].next[j]];
        }
    }
    A = mtPow(A, n);

    LL ret = ;
    for(int i=; i<=tot; i++)
    {
        ret = (ret + A.v[][i]) % MOD;
      //  cout<< ans <<endl;
    }
    printf("%lld\n", ret);

    return ;
}