数据压缩之经典——哈夫曼编码(Huffman)

(笔记图片截图自课程Image and video processing: From Mars to Hollywood with a stop at the hospital的教学视频，使用时请注意版权要求。)

JPEG用哈夫曼编码(Huffman Encoder)作为其符号编码。哈弗曼编码是压缩算法中的经典，它理论上可以将数据编成平均长度最小的无前缀码(Prefix-Free Code)。

为什么要进行编码？

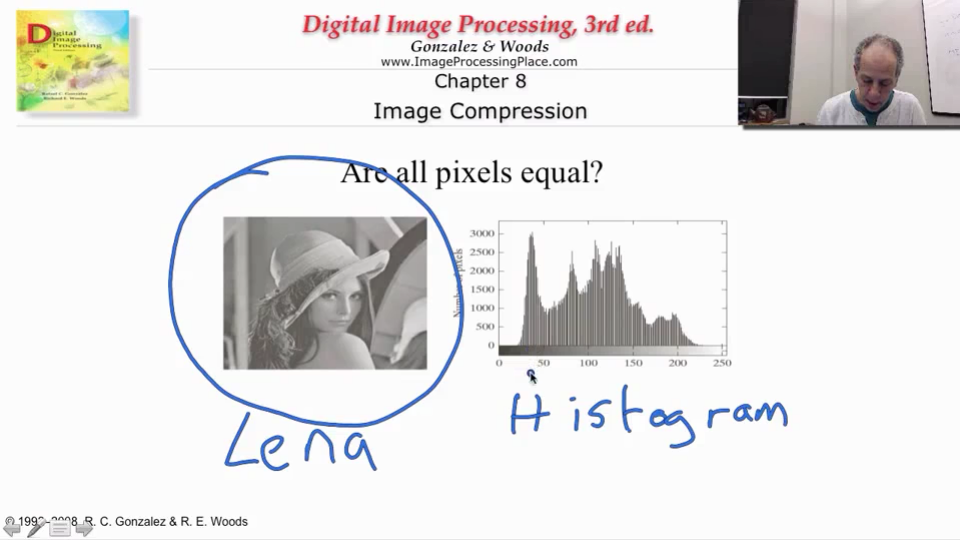
关于Lena：莱娜图（Lenna）是指刊于1972年11月号《花花公子》（Playboy）杂志上的一张裸体插图照片的一部分，是一张大小为512x512像素的标准测试图。该图在数位影像处里学习与研究中颇为知名，常被用作数位影像处里各种实验（例如资料压缩和降噪）及科学出版物的例图。(几乎每一本图像处理相关的书都会出现这张图片~)
Lena的直方图(Histogram)：从Lena的直方图中可以看出，图片中每个灰度值出现的概率是不相同的。这里，中间灰度值部分出现的概率比较高，两边灰度值出现概率非常低。所以，如果每个灰度值都进行同样长度的编码，似乎就太浪费了。

概率高的符号用短码，概率低的符号用长码

正是因为每个灰度值出现的概率不一样，我们用更短的编码来表示经常出现的灰度值，用更长的编码来表示几乎不出现的灰度值，平均下来编码长度就会比等长编码短，从而节省了空间。

Huffman编码生成方式

1. 将要编码的符号按出现概率高到低排列；
2. 将出现概率最低的两个符号进行组合，两者概率加起来得到组合概率；
3. 将得到的组合概率与其他符号的概率再进行排序；
4. 重复(2)，直到出现组合概率为1。

听起来很抽象？实战一次吧。

首先，按照各符号出现概率大小进行排列；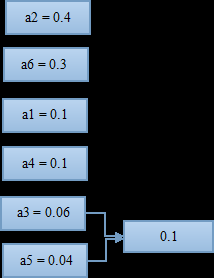

找到概率最小的两个符号，进行组合。这里是a3和a5最小，两者组合起来概率为0.1；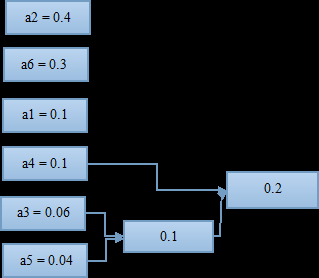

将组合好的两个符号看作一个新的符号，与其他符号再进行一次排列，找到出现概率最小的两个；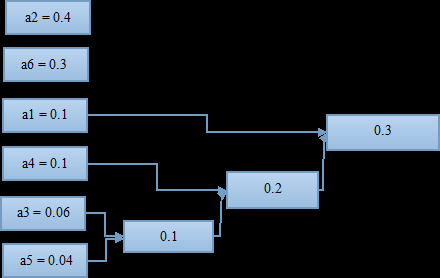

将两个出现概率小的符号再进行一次组合，有得到一个组合概率；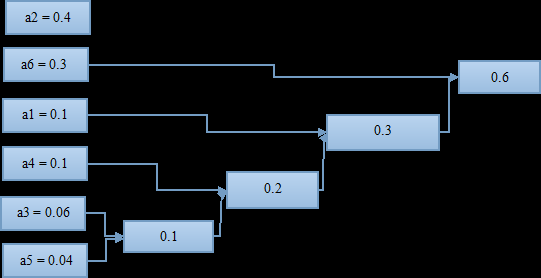

如此进行下去，知道组合到概率为1；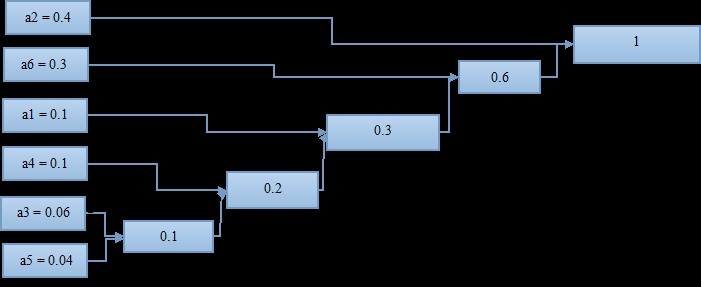

至此，这棵哈夫曼“树”算是画完了，可以进行编码了；
从概率为1(最右)开始，上面分叉编号1，下面分叉编号0(反过来也可以)，编号到最左边。
从右到左读数：

a2 = 1;
a6 = 01;
a1 = 001;
a4 = 0001;
a3 = 00001;
a5 = 00000;

哈夫曼编码的一大好处是，它是Prefix-Free的，也就是每个符号之间不加分隔符，解码器也能识别；
对上面6个符号，如果采用统一长度编码，一个符号需要3bit；
用哈夫曼进行编码，

平均码长 = 1*0.4 + 2*0.3 + 3*0.1 + 4*0.1 + 5*0.06 + 5*0.04 = 2.2bit;
压缩比 = 2.2/3=0.7333333333;

如果概率分布更集中，压缩效果更明显。

理论最小平均码长(信息熵)

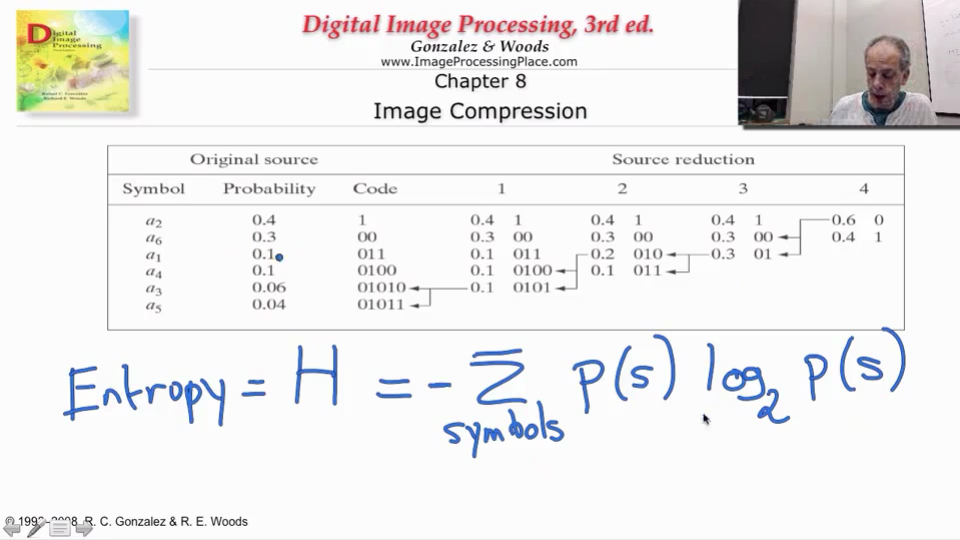
我还依稀记得，香农老人家语重心长地教诲我：哈夫曼编码的最小平均码长，是熵(信息论)。
不过实践经验告诉我，一般哈夫曼编码出来的平均码长，会比这个理论值大那么一丢丢。

三叉Huffman编码方法

经历完上学期的“信息论”考试，我才知道，地球上还存在N叉哈夫曼编码。
一般二叉都会使用二叉哈夫曼编码，也就是用0、1作为分叉。
但考试非要考三叉哈夫曼编码，也就是用0、1、2来进行编码。
方法很简单：方法与二叉Huffman编码一致，如果待编码的符号数不是3的倍数，就自行补上几个“概率为0”的符号，使符号的总个数为3的倍数。

转载：http://mooc.guokr.com/note/5192/