bzoj千题计划263：bzoj4870: [六省联考2017]组合数问题

http://www.lydsy.com/JudgeOnline/problem.php?id=4870

80分暴力打的好爽 \(^o^)/~

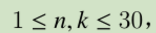
预处理杨辉三角

令m=n*k

要求满足m&x==x ，x<=m， x%k==r 的x的个数

结论：若n&m==m，则C（n，m）为奇数，否则为偶数

枚举m的子集，判断是否%k==r

时间复杂度：O（m的位子集个数），即O（2^(m的二进制中1的个数)）极限是O（n*k）

杨辉三角第i行的和=2^i，即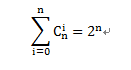

那么用2^(nk) 减去 前面不用的C

因为r<=50，所以这种C的个数<=50

暴力计算C即可

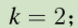
k=2 就是C（2n，r）+C（2n，r+2）+C（2n，r+4）……

是隔一个加一个

杨辉三角 每一行的 奇数列之和=偶数列之和

所以 2^（2n）/2 - 前面不用的C，也是隔一个减一个

除2的计算 要乘2的逆元，但是p不是素数

所以 计算2^(2n) 改成计算 2^(2n-1)

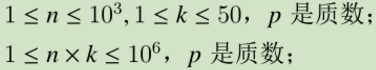
预处理阶乘和阶乘的逆元，枚举计算C ，最多会计算n个C

不会，求指点

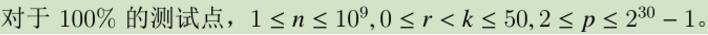
考虑组合数C（n，m）的实际意义：从n个元素里选出m个元素的方案数

那么本题就是求从n*k个元素里，选出%k=r个元素的方案数

dp[i][j] 表示从前i个元素里，选出%k=j 个元素的方案数

第i个不选：dp[i][j]+=dp[i-1][j]

第i个选：dp[i][j]+=dp[i-1][(j-1+k)%k]

矩阵乘法优化

#include<cstdio>
#include<cstring>

using namespace std;

int p,K;

int a[][],ans[][],f[][];

int C[][];

void mul(int A[][],int B[][])
{
    memset(C,,sizeof(C));
    for(int i=;i<K;++i)
        for(int j=;j<K;++j)
            for(int k=;k<K;++k)
                C[i][j]=(C[i][j]+1LL*A[i][k]*B[k][j]%p)%p;
    for(int i=;i<K;++i)
        for(int j=;j<K;++j)
            A[i][j]=C[i][j];
}

int main()
{
    int n,k,r;
    scanf("%d%d%d%d",&n,&p,&K,&r);
    for(int i=;i<=K-;++i) a[i][i]=a[i][i+]=;
    a[K-][K-]++; a[K-][]++;
    f[][]=;
    for(int i=;i<K;++i) ans[i][i]=;
    long long m=1LL*n*K;
    for(;m;mul(a,a),m>>=)
        if(m&) mul(ans,a);
    mul(f,ans);
    printf("%d",f[][r]);
}

AC代码

#include<cstdio>
#include<cstring>

using namespace std;

typedef long long LL;

int n,p,k,r;

int C[][];

int num[];

int inv[],fac[];

LL xx;

void ADD(int &x,int y)
{
    xx=x;
    xx+=y;
    xx-=xx>=p ? p : ;
    x=xx;
}

void YangHui()
{
    C[][]=;
    int m=n*k;
    for(int i=;i<=m;++i)
    {
        C[i][]=;
        for(int j=;j<=m;++j) C[i][j]=(1LL*C[i-][j]+C[i-][j-])%p;
    }
    int ans=;
    for(int i=;i<=n;++i)
    {
        if(i*k+r>m) break;
        ADD(ans,C[m][i*k+r]);
    }
    printf("%d",ans);
}

void Yu()
{
    LL m=1LL*n*k;
    int ans=;
    for(LL t=m;t;t=(t-)&m)
        if(t%k==r) ans^=;
    printf("%d",ans);
}    

int Pow(int a,int b)
{
    int res=;
    for(;b;a=1LL*a*a%p,b>>=)
        if(b&) res=1LL*res*a%p;
    return res;
}

int get_gcd(int a,int b)
{
    return !b ? a : get_gcd(b,a%b);
}

int get_C(int m,int k)
{
    for(int i=m-k+;i<=m;++i) num[i]=i;
    int x,gcd;
    for(int i=;i<=k;++i)
    {
        x=i;
        for(int j=m-k+;j<=m && x!=;++j)
        {
            gcd=get_gcd(num[j],x);
            num[j]/=gcd;
            x/=gcd;
        }
    }
    int ans=;
    for(int i=m-k+;i<=m;++i) ans=1LL*ans*num[i];
    return ans;
}

void PreSum()
{
    int a=Pow(,n);
    int b=;
    for(int i=;i<r;++i) ADD(b,get_C(n,i));
    a-=b;
    if(a<) a+=p;
    printf("%d",a);
}

void JiOu()
{
    int a=Pow(,n*-);
    int b=;
    for(int i=r-;i>=;i-=) ADD(b,get_C(n<<,i));
    a-=b;
    if(a<) a+=b;
    printf("%d",a);
}

int get_inv(int x)
{
    if(inv[x]!=-) return inv[x];
    inv[x]=Pow(fac[x],p-);
    return inv[x];
}

void Cal()
{
    int m=n*k;
    fac[]=;
    for(int i=;i<=m;++i) fac[i]=1LL*fac[i-]*i%p;
    memset(inv,-,sizeof(inv));
    inv[]=;
    int h=r;
    int ans=;
    int tmp;
    for(int i=; h<=m;++i,h+=k)
    {
        tmp=fac[m];
        tmp=1LL*tmp*get_inv(h)%p*get_inv(m-h)%p;
        ADD(ans,tmp);
    }
    printf("%d",ans);
}

int main()
{
    freopen("problem.in","r",stdin);
    freopen("problem.out","w",stdout);
    scanf("%d%d%d%d",&n,&p,&k,&r);
    if(n<= && k<=) YangHui();
     else if(p==) Yu();
    else if(k==) PreSum();
    else if(k==) JiOu();
    else Cal();
    return ;
}

80分暴力

脑抽错误：

C（n，m）一定是偶数，但 对p 取模之后不能保证是偶数

考试的时候没考虑这个 ，直接/2 丢了10分，~~~~(>_<)~~~~