MT【99】2005联赛二试题我的一行解法

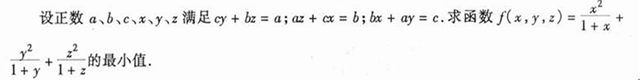
为表示尊敬先展示参考答案：参考答案其实很好的体现了当年出题人陶平生的想法，就是利用已知形式联想到三角里的射影定理，从而写出余弦定理形式，利用三角解题，如下：

这里展示以下几年前做这题时我的解法：

$\sum{\frac{(b^2+c^2-a^2)^2}{4b^2c^2+2bc(b^2+c^2-a^2)}}$

$\ge\sum{\frac{(b^2+c^2-a^2)^2}{4b^2c^2+(b^2+c^2)(b^2+c^2-a^2)}}$

$\ge\frac{[\sum{(b^2+c^2-a^2)}]^2}{4\sum{b^2c^2}+\sum{(b^2+c^2)(a^2+b^2+c^2)}-2\sum{a^2(b^2+c^2)}}$

$=\frac{1}{2}$