POJ 2549 Sumsets（折半枚举+二分）

Sumsets

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 11946		Accepted: 3299

Description

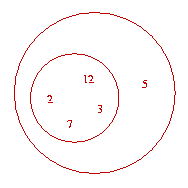Given S, a set of integers, find the largest d such that a + b + c = d where a, b, c, and d are distinct elements of S.

Input

Several S, each consisting of a line containing an integer 1 <= n <= 1000 indicating the number of elements in S, followed by the elements of S, one per line. Each element of S is a distinct integer between -536870912 and +536870911 inclusive. The last line of input contains 0.

Output

For each S, a single line containing d, or a single line containing "no solution".

Sample Input

5
2
3
5
7
12
5
2
16
64
256
1024
0

Sample Output

12
no solution

Source

Waterloo local 2001.06.02

 

题意

给你一个公式a+b+c=d，让你在同一个集合（元素不同）内满足该条件时d的最大值，注意a b c d均不同。

思路

网上折半搜索的思路一般是将a+b+c=d拆分成 a+b=d-c

优秀的代码

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 const int inf = -;
 int a[];
 int main()
 {
     int n;
     while (cin>>n&&n)
     {
         for (int i = ; i < n; i++)
             cin >> a[i];
         sort(a, a + n);//从小到大
         n--;
         int ans = inf;
         for (int i = n; i >= ; i--)
         {
             for (int j = n; j >= ; j--)
             {
                 if (i == j)
                     continue;
                 int sum = a[i] - a[j];
                 for (int l = , r = j - ; l<r;)//剩下用二分
                 {
                     if (a[l] + a[r] == sum)
                     {
                         if (l != i && r != i)
                         {
                             ans = a[i];
                             break;
                         }
                     }
                     if (a[l] + a[r]>sum)
                         r--;
                     else
                         l++;
                 }
                 if (ans != inf)
                     break;
             }
             if (ans != inf)
                 break;
         }
         if (ans == inf)
             printf("no solution\n");
         else
             printf("%d\n", ans);
     }
     return ;
 }

将a+b,c-d看成两个序列，然后二分查找。  注意不要忘记去重

 #include<algorithm>
 #include<cstdlib>
 #include<cstring>
 #include<string>
 #include<stack>
 #include<queue>
 #include<iostream>
 #include<cmath>
 #include<map>
 #include<list>
 #include<stack>
 typedef long long ll;
 using namespace std;  

 int n;
 int a[];  

 struct node{
 int i,j;
 int val;
 }b[*];  

 bool cmp(node a,node b)
 {
     return a.val<b.val;
 }  

 bool comp1(node a,int b)
 {
     return a.val<b;  // 找到第一个val>=b的结构体元素
 }  

 bool comp2(node a,int b)
 {
     return a.val<=b; // 找到第一个val>b的结构体元素
 }  

 int main()
 {
     while(scanf("%d",&n)==&&n)
     {
         int i,j,k,m,t;
         for(i=;i<n;i++)
             scanf("%d",a+i);
         sort(a,a+n);  

         int len=;
         for(i=;i<n;i++)
         {
             for(j=i+;j<n;j++)
             {
                 if(a[i]!=a[j])  //这里直接判断一下 不同的话再存 以后就可以减少这部判断啦
                 {
                     b[len].i=i;
                     b[len].j=j;
                     b[len].val=a[i]+a[j]; //存储题意中的 a+b
                     len++;
                 }
             }
         }
         sort(b,b+len,cmp);  //根据a+b的值从小到大排序  

         bool flag=false;
         for(i=n-;i>=;i--) //之前已经从小到大对sort了 所以直接从最大的开始
         {
             int d=a[i];  //我们要找的d
             for(j=;j<i;j++)
             {
                 if(d!=a[j]) //d不能等于c
                 {
                     int cd=d-a[j];  //cd的值就相当于d-c
                     node* p1=lower_bound(b,b+len,d-a[j],comp1);
                     node* p2=lower_bound(b,b+len,d-a[j],comp2);//注意我写的两个函数comp, 而且都是作为lower_bound的参数
                     if(p2-p1!=)  //说明存在 a+b==d-c
                     {
                         while(p1!=p2) //还要判断一下a,b,c,d是否都不相同
                         {
                             if(a[p1->i]!=a[j]&&a[p1->i]!=a[i]&&a[p1->j]!=a[j]&&a[p1->j]!=a[i])
                             {
                                 flag=true;  //符合题意 直接跳出
                                 break;
                             }
                             p1++;
                         }
                     }
                 }
                 if(flag)  //符合题意 直接跳出
                     break;  

             }
             if(flag)break;  //符合题意 直接跳出  

         }
         if(flag)printf("%d\n",a[i]); //符合题意 直接输出d 也就是a[i]
         else printf("no solution\n");  

     }
   

 #include<cstdio>
 #include<algorithm>
 using namespace std;
 typedef long long ll;
 const int maxn=+;
 ll t[maxn],d[maxn*maxn];
 struct node
 {
     ll sum;
     int use1,use2;
 } c[maxn*maxn];
 bool cmp(const node& a,const node& b)
 {
     return a.sum<b.sum;
 }
 int main()
 {
     int n;
     while(~scanf("%d",&n),n)
     {
         int i,j,s=;
         for(i=; i<n; i++)
             scanf("%lld",&t[i]);
         sort(t,t+n);
         for(i=; i<n; i++)
             for(j=; j<n; j++)
                 if(i!=j)
                 {
                     c[s].sum=t[i]+t[j];
                     c[s].use1=i;
                     c[s++].use2=j;
                 }
         sort(c,c+s,cmp);
         for(i=; i<s; i++)
             d[i]=c[i].sum;
         ll ma=-1e17;
         for(i=; i<n; i++)
         {
             for(j=n-; j>=; j--)
             {
                 if(i!=j&&t[j]>ma)
                 {
                     ll u=-(t[i]-t[j]);
                     int id1=lower_bound(d,d+s,u)-d;
                     int id2=upper_bound(d,d+s,u)-d-;
                     for(int k=id1;k<id2;k++)
                     {
                         int a=c[k].use1,b=c[k].use2;
                         if(a!=i&&a!=j&&b!=i&&b!=j)
                         {
                             ma=t[j];break;
                         }
                     }
                 }
             }
         }
         if(ma!=-1e17)printf("%lld\n",ma);
         else printf("no solution\n");
     }
     return ;
 }