RUAL1519 Formula 1 【插头DP】

RUAL1519 Formula 1

---

Background

Regardless of the fact, that Vologda could not get rights to hold the Winter Olympic games of 20**, it is well-known, that the city will conduct one of the Formula 1 events. Surely, for such an important thing a new race circuit should be built as well as hotels, restaurants, international airport - everything for Formula 1 fans, who will flood the city soon. But when all the hotels and a half of the restaurants were built, it appeared, that at the site for the future circuit a lot of gophers lived in their holes. Since we like animals very much, ecologists will never allow to build the race circuit over the holes. So now the mayor is sitting sadly in his office and looking at the map of the circuit with all the holes plotted on it.

Problem

Who will be smart enough to draw a plan of the circuit and keep the city from inevitable disgrace? Of course, only true professionals - battle-hardened programmers from the first team of local technical university!.. But our heroes were not looking for easy life and set much more difficult problem: “Certainly, our mayor will be glad, if we find how many ways of building the circuit are there!” - they said.

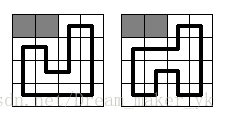
It should be said, that the circuit in Vologda is going to be rather simple. It will be a rectangle N*M cells in size with a single circuit segment built through each cell. Each segment should be parallel to one of rectangle’s sides, so only right-angled bends may be on the circuit. At the picture below two samples are given for N = M = 4 (gray squares mean gopher holes, and the bold black line means the race circuit). There are no other ways to build the circuit here.

Input

The first line contains the integer numbers N and M (2 ≤ N, M ≤ 12). Each of the next N lines contains M characters, which are the corresponding cells of the rectangle. Character “.” (full stop) means a cell, where a segment of the race circuit should be built, and character “*” (asterisk) - a cell, where a gopher hole is located. There are at least 4 cells without gopher holes.

Output

You should output the desired number of ways. It is guaranteed, that it does not exceed 263-1.

Samples

Input

4 4

**..

….

….

….

Output

2

Inpuut

4 4

….

….

….

….

Output

6

---

大概是插头DP的板子题

用Hash表储存状态

然后分别讨论当前的插头所对应的轮廓线上插头的情况

具体的在插头DP的总结里边写一些吧

然后根据已有的插头状态考虑当前位置的情况，大致分为连接，延长，新建三种

然后发现状态比较多，用四进制来进行储存，反正位运算快嘛

---

#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define MAX 300010
#define N 20
int n,m,ind,endx,endy;
int mp[N][N],tot[2],bit[N];
LL dp[2][MAX],state[2][MAX],sum;
int head[MAX],Next[MAX],Hash[MAX],siz;
/*
tot 状态数
state 每个状态是什么
Hash hash表
*/
void init(){
    memset(mp,0,sizeof(mp));
    sum=ind=0;
    tot[ind]=1;
    dp[ind][1]=1;
    state[ind][1]=0;
}
void Insert(LL s,LL num){
    int pos=s%MAX;
    for(int i=head[pos];~i;i=Next[i])
        if(state[ind][Hash[i]]==s){dp[ind][Hash[i]]+=num;return;}
    ++tot[ind];
    state[ind][tot[ind]]=s;
    dp[ind][tot[ind]]=num;
    Hash[siz]=tot[ind];
    Next[siz]=head[pos];
    head[pos]=siz++;
}
void DP(){
    for(int i=1;i<=n;i++){
        for(int k=1;k<=tot[ind];k++)state[ind][k]<<=2;
        for(int j=1;j<=m;j++){
            memset(head,-1,sizeof(head));siz=0;
            ind^=1;tot[ind]=0;
            for(int k=1;k<=tot[ind^1];k++){
                LL s=state[ind^1][k];
                LL num=dp[ind^1][k];
                int p=(s>>bit[j-1])%4;//左
                int q=(s>>bit[j])%4;//上
                if(!mp[i][j]){if(p+q==0)Insert(s,num);}
                else if(p+q==0){//上左都没有插头
                    if((!mp[i+1][j])||(!mp[i][j+1]))continue;
                    s=s+(1<<bit[j-1])+2*(1<<bit[j]);
                    Insert(s,num);
                }else if(p==0&&q){
                    if(mp[i][j+1])Insert(s,num);
                    if(mp[i+1][j]){
                        s=s+q*(1<<bit[j-1])-q*(1<<bit[j]);
                        Insert(s,num);
                    }
                }else if(p&&q==0){
                    if(mp[i+1][j])Insert(s,num);
                    if(mp[i][j+1]){
                        s=s-p*(1<<bit[j-1])+p*(1<<bit[j]);
                        Insert(s,num);
                    }
                }else if(p+q==2){
                    int b=1;
                    for(int t=j+1;t<=m;t++){
                        int v=(s>>bit[t])%4;
                        if(v==1)++b;
                        if(v==2)--b;
                        if(!b){s-=(1<<bit[t]);break;}
                    }
                    s=s-(1<<bit[j-1])-(1<<bit[j]);
                    Insert(s,num);
                }else if(p+q==4){
                    int b=1;
                    for(int t=j-2;t>=0;--t){
                        int v=(s>>bit[t])%4;
                        if(v==2)++b;
                        if(v==1)--b;
                        if(!b){s+=(1<<bit[t]);break;}
                    }
                    s=s-2*(1<<bit[j-1])-2*(1<<bit[j]);
                    Insert(s,num);
                }else if(p==1&&q==2){
                    if(i==endx&&j==endy)sum+=num;
                }else if(p==2&&q==1){
                    s=s-2*(1<<bit[j-1])-(1<<bit[j]);
                    Insert(s,num);
                }
            }
        }
    }
}
int main(){
    for(int i=0;i<N;i++)bit[i]=i<<1;
    while(scanf("%d%d",&n,&m)!=EOF){
        init();
        for(int i=1;i<=n;i++){
            getchar();char ch;
            for(int j=1;j<=m;j++){
                scanf("%c",&ch);
                mp[i][j]=(ch=='.');
                if(ch=='.')endx=i,endy=j;
            }
        }
        DP();
        printf("%lld\n",sum);
    }
    return 0;
}