NOIP模拟赛
T1
1.聪明的小偷
(thief.pas/c/cpp)
【问题描述】
从前有一个收藏家收藏了许多相同的硬币,并且将它们放在了n个排成一排的口袋里,每个口袋里都装了一定数量的硬币。
这些硬币价值不菲,自然引起不少人觊(ji,4)觎(yu,2),于是收藏家每天都会来检查一次这n个口袋,首先他会先检查每个口袋是不是都有硬币,之后他会计算出第1个和第2个口袋的硬币数量之和,第2个与第3个口袋的硬币数量和,如此直到第n-1个与第n个口袋的硬币数量之和,得到n-1个数的序列。
如果收藏家发现某个口袋没有硬币,或者他计算得到的序列较上一天相比有变动,那么收藏家就知道肯定有人动了他的硬币。
有一个聪明的小偷,他想在收藏家不知道的情况下偷走一些硬币,为此,他不仅可以偷偷地从某个口袋中拿出一些硬币,也可以将硬币在口袋间任意移动,现在他想知道对于给定的n个口袋及对应的硬币数量,他最多能拿多少枚硬币。
小偷是很聪明的,他早就算出来啦,但是他想考考作为徒弟的你……
【数据规模与约定】
对于50%的数据,有2≤n≤20,每个口袋中硬币数量≤20。
对于100%的数据,有2≤n≤999,每个口袋中硬币数量≤10000且为正整数。
贪心提,自己造了几组数据,连蒙带猜找到规律就可以了
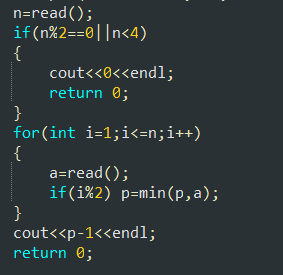
当n为偶数时,答案一定为 0,当 n为奇数时,答案为所有编号为奇数的口袋中硬币数量的最小值 -1。
注:n<=3时奇数也不行
T2
2.无名
(noname.pas/c/cpp)
【问题描述】
这道题实在不知道该取什么名字比较好,于是就取了这个名字。
给定一个长度为n的正整数序列,你的任务就是求出至少需要修改序列中的多少个数才能使得该数列成为一个严格(即不允许相等)单调递增的正整数序列,对序列中的任意一个数,你都可以将其修改为任意的正整数。
【数据规模与约定】
对于30%的数据,有1≤n≤10。
对于80%的数据,有1≤n,T≤50,且输入序列中每个数均不超过50。
对于100%的数据,有1≤n≤50000,1≤T≤5000,输入序列中每个数均为不超过1000000000(10^9)的正整数,且每个测试点中T组数据对应的n值总和不超过500000。
看到数据范围就果断选择80分算法
80分:
DP
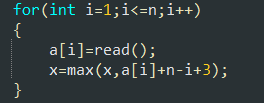
f[i][j] 代表前i个数最后一位为j时的最小改变策略

x 表示可以任意数变到的最大值
正解:
简单来说就是:构造序列b[i] = a[i] – i;答案即为序列总长度减去B的最长不下降子序列。
(nlogn)二分优化lis
T3
3.服务
(service.pas/c/cpp)
【问题描述】
一家公司为它在各地的用户提供服务,公司有三名负责这项工作的员工,分别编号为1,2,3,服务的地点有n个,分别编号为1,2,3,...n,把从编号为p的服务地点直接到达编号为q的服务地点所需的移动费用记为C(p,q),显然C(p,p)=0(停留在原地不需要费用),但不保证对任意p,q均有C(p,q)=C(q,p)。
初始时员工1在地点1,员工2在地点2,员工3在地点3,现在公司依次收到了L个服务请求,每个请求需要一名员工赶到其指定的地点进行服务,员工可以选择直达,也可以选择经过若干个服务地点中转,特别地,如果指派的员工已在当前请求所在地,则该请求不需要任何移动费用即可被处理。
出于公平起见,所有请求必须按顺序处理,这意味着即使一名员工在赶往当前请求的途中经过之后的请求所在的地点,他也不可以先处理之后的请求,但是公司不限制每位员工赶往请求地点的路线,也允许一个服务地点有多名员工。
你的任务就是对于这L个请求,找到一个服务方案(即对每个请求分配合适的员工去服务以及规划移动路线),使得三名员工提供服务的总移动费用最小。
【数据规模与约定】
每个测试点5分,各个测试点数据范围如下:
|
测试点编号 |
n |
L |
|
1-3 |
||
|
4-6 |
||
|
7-10 |
||
|
11-14 |
||
|
15-17 |
||
|
18-20 |
对于所有的测试点,均有数据组数,地点数,给定的C矩阵主对角线上的数全部为0,且输入数据中所有的数均为不超过2000的非负整数。
从考试开始到结束都没想过4维的DP
打了不知道多长时间的暴力后 果断放弃提交()
正解:
首先用Floyd求最短路。
4 维 DP f[k][i1][i2][i3] 代表做到第 k 个任务是3人在 i1 i2 i3 时的费用。
5重循环。
优化
因为有任务,所以可已确定完成这个任务前后某个人的位置 完成第 k 个任务前一定有一个人在 b[k1-1] 的位置 完成第 k 个任务后一定有一个人在 p[k1] 的位置。所以就能剩一冲循环了(4重)。
因为可以确定某个人的位置,所以可以再省略一维 i3。i1,i2都不到p[k1]的位值,i3一定就在;i1或 i2到 b[k1]的位值,i3一定就不在;
所以:并列3个核心
注:初始化f[0][1][2]=0;
b[0]=3;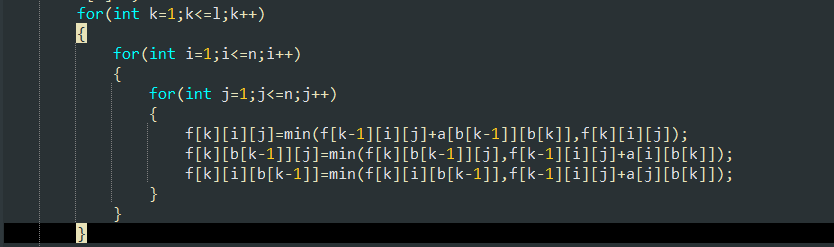
NOIP模拟赛的更多相关文章
- NOIP模拟赛20161022
NOIP模拟赛2016-10-22 题目名 东风谷早苗 西行寺幽幽子 琪露诺 上白泽慧音 源文件 robot.cpp/c/pas spring.cpp/c/pas iceroad.cpp/c/pas ...
- contesthunter暑假NOIP模拟赛第一场题解
contesthunter暑假NOIP模拟赛#1题解: 第一题:杯具大派送 水题.枚举A,B的公约数即可. #include <algorithm> #include <cmath& ...
- NOIP模拟赛 by hzwer
2015年10月04日NOIP模拟赛 by hzwer (这是小奇=> 小奇挖矿2(mining) [题目背景] 小奇飞船的钻头开启了无限耐久+精准采集模式!这次它要将原矿运到泛光之源的矿 ...
- 大家AK杯 灰天飞雁NOIP模拟赛题解/数据/标程
数据 http://files.cnblogs.com/htfy/data.zip 简要题解 桌球碰撞 纯模拟,注意一开始就在袋口和v=0的情况.v和坐标可以是小数.为保险起见最好用extended/ ...
- 队爷的讲学计划 CH Round #59 - OrzCC杯NOIP模拟赛day1
题目:http://ch.ezoj.tk/contest/CH%20Round%20%2359%20-%20OrzCC杯NOIP模拟赛day1/队爷的讲学计划 题解:刚开始理解题意理解了好半天,然后发 ...
- 队爷的Au Plan CH Round #59 - OrzCC杯NOIP模拟赛day1
题目:http://ch.ezoj.tk/contest/CH%20Round%20%2359%20-%20OrzCC杯NOIP模拟赛day1/队爷的Au%20Plan 题解:看了题之后觉得肯定是DP ...
- 队爷的新书 CH Round #59 - OrzCC杯NOIP模拟赛day1
题目:http://ch.ezoj.tk/contest/CH%20Round%20%2359%20-%20OrzCC杯NOIP模拟赛day1/队爷的新书 题解:看到这题就想到了 poetize 的封 ...
- CH Round #58 - OrzCC杯noip模拟赛day2
A:颜色问题 题目:http://ch.ezoj.tk/contest/CH%20Round%20%2358%20-%20OrzCC杯noip模拟赛day2/颜色问题 题解:算一下每个仆人到它的目的地 ...
- CH Round #52 - Thinking Bear #1 (NOIP模拟赛)
A.拆地毯 题目:http://www.contesthunter.org/contest/CH%20Round%20%2352%20-%20Thinking%20Bear%20%231%20(NOI ...
- CH Round #49 - Streaming #4 (NOIP模拟赛Day2)
A.二叉树的的根 题目:http://www.contesthunter.org/contest/CH%20Round%20%2349%20-%20Streaming%20%234%20(NOIP 模 ...
随机推荐
- 快速上手Runtime(三)之方法交换
开发过程中,我们经常会用到系统类,而它提供的方法又不能完全满足我们开发的需要,那么在此时,我们需要为系统自带的方法扩展一些功能,而且还要保证原有的功能可正常使用.假设咱们现在有这么一个需求,我们在调用 ...
- 801. Minimum Swaps To Make Sequences Increasing 为使两个数组严格递增,所需要的最小交换次数
[抄题]: We have two integer sequences A and B of the same non-zero length. We are allowed to swap elem ...
- Linux系统中当前路径不加入PATH的原因
主要是出于安全的考虑,由于系统默认是允许所有人在/tmp下写入任何文件的,万一有居心不良的用户或者黑客入侵到计算机,并在/tmp下面埋下木马,名字为ls,当用户用root身份登录后,到/tmp目录执行 ...
- 解决VirtualBox 上的XP 关机时重启 , 启动时蓝屏 ,点击电源选项蓝屏
三个问题一次性解决. 启动时的蓝屏显示错误信息是: STOP 0x000000CE (...) DRIVER_UNLOADED_WITHOUT_CANCELLING_PENDING_OPERATION ...
- Windows查看端口占用及杀掉进程
"到底是谁占用了80端口,该怎么查,怎么终止它?",这里就简单讲解一下,在windows下如何查看80端口占用情况?是被哪个进程占用?如何终止等.这里主要是用到windows下的D ...
- maven 执行本地、服务器 jar包安装
开发时遇到过第三方jar包依赖不了时的尴尬 因为遇到过几次所以记录一下,POM文件引入的个推jar包无效,就必须本地安装了,服务器上的也是一样,执行相同的maven命令就行,注意修改路径!和将jar包 ...
- CMDB小练习
为什么要用CMDB? 因为公司之前统计资产信息用的是excel表格,随着业务的增加和信息的变更,这个表格变得越来越乱,所以我们就想着编写出一套自动管理资产信息的系统,实现自动管理资产信息 三种方案? ...
- java网站如何集成facebook第三方登录
第一次接触Facebook第三方登录,可能有些地方做的并不全面,只是尝试着做了一个小demo,因为国内接入Facebook的项目并不多,并且多数都是Android或iOS的实现,所以资料也特别少,在此 ...
- Ubuntu重复循环启动的快速解决方法
如果因为在配置java或者adb环境变量时修改profile文件导致的在登录界面输入密码后重复循环启动的问题,下面总结网上和实践找到快速解决的方法啦! 1.在登录界面按下ctrl+alt+F1进入命令 ...
- pig(数据流语言和编译器)学习https://www.w3cschool.cn/apache_pig/apache_pig_execution.html
当我们配置了hadoop集群执行的时候 可以通过命令ls进行查看 存储语法 STORE Relation_name INTO ' required_directory_path ' [USING fu ...
