Petrozavodsk Summer Training Camp 2017 Day 9

Petrozavodsk Summer Training Camp 2017 Day 9

Problem A. Building

题目描述：给出一棵树，在树上取出一条简单路径，使得该路径的最长上升子序列最长，问最长的长度。

solution
最常见的想法就是树状dp，但空间不太够，所以选择直接计数。

每个点记住两个\(vector(f, g)\)，\(f_i\)表示从叶子到\(i\)的最长的递增序列，\(g_i\)表示从叶子到\(i\)的最长的递减序列。

当算以\(i\)为根的子树的答案时，假设做到儿子\(j\)，算\(f[i]\)与\(g[j]\)组成的最长递增序列，以及\(f[j]\)与\(g[i]\)的最长递增序列。算的时候一个序列枚举每个数，然后在另一个序列二分出位置，即可更新答案，而枚举的序列要选短的那个，这样时间复杂度就能保证为\(log^2n\)，还要注意答案序列经过\(i\)的情况。

然后就是将\(f[i]、f[j]\)，\(g[i]、g[j]\)合并。拿\(f[i]、f[j]\)合并为例子，合并的时候直接取对应位置的最小值即可，即：

2 3 4 6 7
1 2 5 8

合并为1 2 4 6 7.
对于\(f\)序列，数越小越好，因为对于相同的位置\(k\)，它在答案序列的位置就是\(k\)，这是固定的，而数越小，就可以在\(g\)找到更多的数来拼成序列，得到更大的答案。
同样的道理，对于\(g\)中的数找\(f\)对应的位置，对于相同的数，\(f\)的数越小，二分出的位置不会更差，反而有可能更优。
因此对于\(g\)序列，数越大越好。

时间复杂度：\(O(nlog^2n)\)

Problem B. Fish

题目描述：有\(n\)条鱼，每条鱼的长度为\(L_i\)，颜色是\(c_i\)，颜色只有三种('R', 'G', 'B')。现要取出一个非空子集，使得任意一条鱼的长度小于任意一条鱼的长度的两倍，假设选出的子集的每种颜色数目为三元对\((x, y, z)\)，问三元对的数目。

solution
将鱼按长度从小到大排序，对于每条鱼\(i\)，找到最大的\(j\)，满足\(L_j<L_i*2\)，部分和求出\([i, j]\)的每种颜色的数目\((x_i, y_i, z_i)\)。问题转化为有\(n\)个三元对\((x_i, y_i, z_i)\)，求三元对\((x, y, z)\)的数目，满足存在一个\(i\)，\(x \leq x_i, y \leq y_i, z \leq z_i\)。

这就跟codeforces上的一道题很像(Karen and Cards)，至少思路很像。

这里我们将三元对从大到小排序，记每个\(y\)对应的最大的\(z\)为\(maxz[y]\)。对于每一个\(x\)，用\(x_i==x\)的三元对更新\(maxz[y]\)，这里要利用\(maxz[y]\)的一个特点：\(maxz[y]\)是递减。所以可以二分出要更新的区间，然后用线段树维护\(maxz[y]\)。然后对于\(x\)，答案就是\(\sum maxz[y]\)。

时间复杂度：\(O(nlogn)\)

Problem C. JOI Flag

题目描述：定义\(level-K\)的\(JOI Flag\)：

1. 一个\(level-0\)的\(JOI Flag\)是一个\(1 \times 1\)的网格图，包含'J', 'O', 'I'其中一个字母。
2. 当\(m>0\)时，一个\(level-m\)的\(JOI Flag\)是一个\(2^m \times 2^m\)的网格图，能分成四个\(2^{m-1} \times 2^{m-1}\)的网格图：一个是\(level-m-1\)的\(JOI Flag\)，一个全是'J', 一个全是'O'，一个全是'I'。
   现在有一个\(2^K \times 2^K\)的网格图，里面有些格子的字母是确定的，未知的位置可以随便填字母而不需要花费，改变已知的字母则需要花费\(1\)。问将这个网格图变成一个\(level-K\)的\(JOI Flag\)需要的最小花费。

solution
因为已知的字母比较少，所以可以直接暴力搜索。

时间复杂度：\(O(4!NK)\)

Problem E. Rotate

题目描述：给出一个\(N \times N\)的网格图，每个格子有一个小写字母。现在有\(Q\)次操作，每次操作选择一个子方阵，将子方阵逆时针旋转\(90^{\circ}\)。输出最后的网格图。

solution
一开始的想法是将每一行，每一列压位，然后暴力旋转，时间复杂度是\(O(QN^2/13)\)。但写起来非常恶心。

在网格图外围再围一层，变成\((N+2) \times (N+2)\)的网格图，然后从\(0\)到\(n*n-1\)编号\((n=N+2)\)，记录每个编号\(i\)，左上右下的编号。

当进行一次旋转操作时，只有子方阵的边界的左上右下的编号会改变，子方阵内部的也会改变，但改变的只是编号对应的方向，也就是说还是那四个编号，只是方向发生了改变，而且这个改变是轮换，即方向的相对位置没有发生变化。例如：

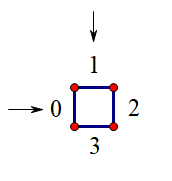
只要是沿当前方向向前走，不管是从\(0\)进来还是\(1\)进来，都是从\(+2\)的位置出去，只要是右拐，都是从\(-1\)的位置出去。所以每次只需要修改子方阵边界的各个方向的编号，内部的不需要修改。

定位子方阵的左上角时，从\(0\)开始向右走（最外围不会被改变），走到对应列右拐，向前走走到对应行，然后围着子矩阵边界转一圈。注意这里行走时用的描述都是向前，拐弯，不是上下左右，因为只能保证相对位置不变，去哪一个编号也跟从哪里来有关。输出答案时从每一行的边界开始向右（最左边一列不变）前进即可。

时间复杂度：\(O(QN)\)

Problem F. Fortune Telling

题目描述：有一个\(M \times N\)的网格图，每个格子开始时都是白色，现在有\(K\)个操作，每次操作将一个子矩阵的颜色翻转，即黑变白，白变黑。问最终有多少个格子是白色。

solution
离散化+扫描线+线段树。

时间复杂度：\(O(nlogn)\)

Problem G. Kangaroo

题目描述：有\(n\)只袋鼠，每只袋鼠的大小为\(A_i\)，袋子的大小为\(B_i\)。每只袋鼠只能装一只袋鼠，但允许那只袋鼠的袋子里也有袋鼠，当\(A_j<B_i\)时，袋鼠\(j\)就能装到\(i\)的袋子里。问最后的状态有多少种（能装就要装）。

solution
转队友的题解

Problem I. Chinese

题目描述：在圆桌上等分地放着\(n\)盘菜，顺时针或逆时针旋转一个单位需要一个花费。现在给出\(2\)~\(n\)每个人要吃的菜，开始时第\(i\)个人对着第\(i\)盘菜，第一个人最先吃（对着就能吃），吃完后其他人再吃，其他人吃时不分顺序，输出当第一个人吃第\(i\)盘菜时，所有人吃完菜的最少花费。

solution
算出从初始开始顺时针转，使得第\(i\)个人吃上菜的花费\(a_i\)，因为是环，惯用技巧是将\(a\)数组复制一遍在后面。
枚举\(i\)(\(1\)~\(2*n-1\))表示第一个人吃第\(i\)盘菜，求出\(j\)使得\(\sum_{k=i}^{j} a_k==n-1\)，则\(j-i\)是一种方案，假设\(x\)为\(i-1\)时的最优方案，则\(x+1\)也是一种方案，即花费\(1\)转回去，然后用\(i-1\)时的最优方案。
反过来枚举\(i\)(\(2*n\)~\(1\))，然后按上述的做法重做一次，表示逆时针转。
这两种方法已经涵盖了所有的最优方案。当第一个人吃第\(i\)盘菜时，方案有四个：1、顺时针转，2、逆时针转，3、先顺时针转再逆时针转，4、先逆时针转再顺时针转。而上述方法中的花费\(1\)转回去，就是方案3、4。

时间复杂度：\(O(n)\)