LEETCODE —— Linked List Cycle [Floyd's cycle-finding algorithm]

Linked List Cycle

Given a linked list, determine if it has a cycle in it.

Follow up:
Can you solve it without using extra space?

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def hasCycle(self, head):
        """
        :type head: ListNode
        :rtype: bool
        """
        if head is None:
            return False
        rabbit = turtle = head
        while rabbit.next and rabbit.next.next:
            turtle = turtle.next
            rabbit = rabbit.next.next
            if rabbit == turtle:
                return True
        return False

 解法，两个指针同时前移，当二者碰面则为有环，遇到None则为无环。 i.e.

佛洛依德龟兔算法

 这个猜想其实早就被证明了，wiki: http://en.wikipedia.org/wiki/Cycle_detection#Tortoise_and_hare ，so更详细的解释在此：

 

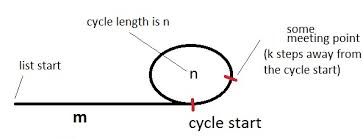
Let me try to clarify the cycle detection algorithm that is provided at http://en.wikipedia.org/wiki/Cycle_detection#Tortoise_and_hare in my own words. I refer to the figure  in my explanation. How it works Let's have a tortoise and a hare (name of the pointers) pointing to the beginning of the list with a cycle. Let's hypothesize that if we move tortoise 1 step at a time, and hare 2 steps at a time, they will eventually meet at a point. Let's show that first of all this hypothesis is true. The figure illustrates a list with a cycle. The cycle has a length of n and we are initially m steps away from the cycle. Also let's say that the meeting point is k steps away from the cycle beginning and tortoise and hare meets after a total of i steps. The following 2 conditions must hold: 1) i = m + p * n + k 2) 2i = m + q * n + k The first one says that tortoise moves i steps and in these i steps it first gets to the cycle. Then it goes through the cycle p times for some positive number p. Finally it goes over k more nodes until it meets hare. A similar is true for hare. It moves 2i steps and in these 2i steps it first gets to the cycle. Then it goes through the cycle q times for some positive number q. Finally it goes over k more nodes until it meets tortoise. Therefore, 2 ( m + p * n + k ) = m + q * n + k => 2m + 2pn + 2k = m + nq + k => m + k = ( q - 2p ) n Among m, n, k, p, q, the first two are properties of the given list. If we can show that there is at least one set of values for k, q, p that makes this equation true we show that the hypothesis is correct. One such solution set is as follows: p = 0 q = m k = m n - m We can verify that these values work as follows: m + k = ( q - 2p ) n => m + mn - m = ( m - 2*0) n => mn = mn. For this set, i is i = m + p n + k => m + 0 * n + mn - m = mn. Of course, you should see that this is not necessarily the smallest i possible. In other words, tortoise and hare might have already met before many times. However, since we show that they meet at some point at least once we can say that the hypothesis is correct. So they would have to meet if we move one of them 1 step, and the other one 2 steps at a time. Now we can go to the second part of the algorithm which is how to find the beginning of the cycle. Cycle Beginning Once tortoise and hare meet, let's put tortoise back to the beginning of the list and keep hare where they met (which is k steps away from the cycle beginning). The hypothesis is that if we let them move at the same speed (1 step for both), the first time they ever meet again will be the cycle beginning. Let's prove this hypothesis. Let's first assume some oracle tells us what m is. Then, if we let them move m + k steps, tortoise would have to arrive at the point they met originally (k steps away from the cycle beginning - see in the figure). Previously we showed that m + k = (q - 2p) n. Since m + k steps is a multiple of cycle length n, hare, in the mean time, would go through the cycle (q-2p) times and would come back to the same point (k steps away from the cycle beginning). Now, instead of letting them move m + k steps, if we let them move only m steps, tortoise would arrive at the cycle beginning. Hare would go be k steps short of completing (q-2p) rotations. Since it started k steps in front of the cycle beginning, hare would have to arrive at the cycle beginning. As a result, this explains that they would have to meet at the cycle beginning after some number of steps for the very first time (very first time because tortoise just arrived at the cycle after m steps and it could never see hare which was already in the cycle). Now we know that the number of steps we need to move them until they meet turns out to be the distance from the beginning of the list to the cycle beginning, m. Of course, the algorithm does not need to know what m is. It will just move both tortoise and hare one step at a time until they meet. The meeting point has to be the cycle start and the number of steps must be the distance (m) to the cycle beginning. Assuming we know the length of the list, we can also, compute the length of the cycle of subtracting m from the list length.