2016ACM/ICPC亚洲区沈阳站-重现赛

C.Recursive sequence

求ans(x),ans(1)=a,ans(2)=b,ans(n)=ans(n-2)*2+ans(n-1)+n^4

如果直接就去解。。。很难，毕竟不是那种可以直接化成矩阵的格式，我们也因为这个被卡很长时间

事实上可以把这道式子化成几个基本元素的格式，然后就容易组合了，比如ans(n-2)*2+ans(n-1)+(n-1)^4+4*(n-1)^3+6*(n-1)^2+4*(n-1)^1+1

包含了所有的基本组成形式，化绝对为相对，并且除了一个n-2其他都是n-1

然后就是矩阵乘时间了

#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#include <iostream>
#include <cstring>

using namespace std;

typedef long long int ll;
const ll mod = ;

//定义矩阵乘法
struct matrix{
    ll arr[][];
    matrix operator*(matrix b){
        matrix ans;
        ll tmp;
        for(int i=; i<; i++)
            for(int j=; j<; j++){
                ans.arr[i][j] = ;
                for(int k=; k<; k++){
                    tmp = (arr[i][k]*b.arr[k][j])%mod;
                    ans.arr[i][j] = (ans.arr[i][j] + tmp)%mod;
                }
            }
        return ans;
    }
};

//矩阵快速幂
matrix quick_pow(matrix a,ll N){
    matrix ans;
    memset(ans.arr,,sizeof(ans.arr));
    for(int i=; i<; i++)
        ans.arr[i][i] = ;
    while(N){
        if(N&)
            ans = ans*a;
        a = a*a;
        N /= ;;
    }
    return ans;
}

int main(){

    matrix a;
    memset(a.arr,,sizeof(a.arr));
    a.arr[][] = ;
    a.arr[][] = a.arr[][] = a.arr[][] = ;
    a.arr[][] = a.arr[][] = ;
    a.arr[][] = ; a.arr[][] = a.arr[][] = a.arr[][] = a.arr[][] = ;
    a.arr[][] = a.arr[][] = ;
    a.arr[][] = a.arr[][] = a.arr[][] = a.arr[][] = ;
    a.arr[][] = a.arr[][] = a.arr[][] = ;
    a.arr[][] = a.arr[][] = ;
    a.arr[][] = ;
    int T;
    scanf("%d",&T);
    ll N,aa,bb;
    while(T--){
        scanf("%I64d %I64d %I64d",&N,&aa,&bb);
        if(N==)
            printf("%I64d\n",aa);
        else if(N==)
            printf("%I64d\n",bb);
        else{
            matrix ans = quick_pow(a,N-);
            ll ANS = ;
            ANS = (ANS+ans.arr[][]*aa)%mod;
            ANS = (ANS+ans.arr[][]*bb)%mod;
            ANS = (ANS+ans.arr[][]*)%mod;
            ANS = (ANS+ans.arr[][]*)%mod;
            ANS = (ANS+ans.arr[][]*)%mod;
            ANS = (ANS+ans.arr[][]*)%mod;
            ANS = (ANS+ans.arr[][]*)%mod;
            printf("%I64d\n",ANS);
        }
    }
    return ;
}

G.Do not pour out

注：我不会在电脑写希腊字符，西塔会写成0-

有直径2，高度2的圆柱体杯子，装d高度的水，把杯子倾倒至水正好不倒出，水面碰着杯沿，问此时水面面积

d==0时S=0，样例给出

d>=1时，水面椭圆是宽径为1，长径为2tan0-的椭圆，根据面积公式S=pi*length*width=pi/cos0-出解

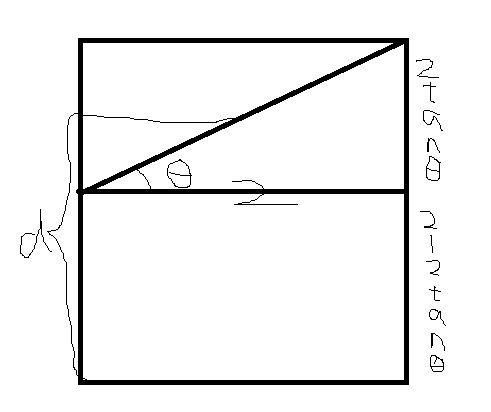
0<d<1时，水面被杯底截断，只能用积分做。

把下述直线右边当做水的截面，一个个积分（岂可修！这么简单！为什么比赛时没想到呢！哎，都怪我被体积蒙蔽了）

V=(0<=y<=2)∫S0dy

S0=pi-a+k*1sina

cosa=k/1

k+1=ytan0-

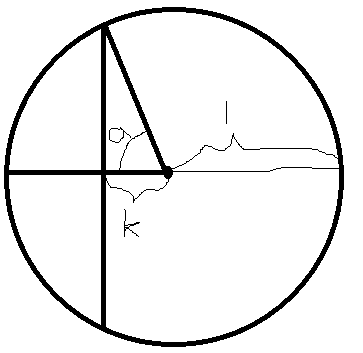
V=(0<=y<=2)∫S0dy

=(0<=y<=2)∫pi-a+cosasinady

=(pi<=y<=a1)1/tan0-*∫(pi-a+cosasina)(-sina)da

a1=arccos(2tan0--1)

手动转换和确定值间太费时了，还是二分把，反正数据量也不是很多，答案是S=s0/sin0-

/*--------------------------------------------
 * File Name: HDU 5954
 * Author: Danliwoo
 * Mail: Danliwoo@outlook.com
 * Created Time: 2016-11-01 22:22:15
--------------------------------------------*/

#include <bits/stdc++.h>
using namespace std;
double Pi = acos(-1.0);
double eps = 1e-;
double tran = /Pi;
double vd;
double V(double a) {
    return Pi*cos(a) - a*cos(a) + sin(a) - pow(sin(a), )/;
}
double get(double theta) {
    double a1 = acos(*tan(theta)-);
    double v = (V(a1) - V(Pi))/tan(theta);
    return v;
}
bool eq(double x, double y) {
    return fabs(x-y) < eps;
}
double find(double l, double r) {
    int cnt = ;
    if(eq(get(l), vd)) return l;
    while(cnt--) {
        double mid = (l+r) / ;
        double gd = get(mid);
        if(eq(gd, vd)) return mid;
        if(gd > vd) r = mid;
        else l = mid;
    }
    return l;
}
int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        double d;
        scanf("%lf", &d);
        vd = d * Pi;
        if(eq(d, )) {
            printf("0.00000\n");
            continue;
        }
        if(d -  > ) {
            double theta = atan(2.0-d);
            double ans = Pi/cos(theta);
        //  printf("d>1 theta = %.5f\n", theta*tran);
            printf("%.5f\n", ans);
            continue;
        }
        double theta = find(eps, Pi/);
        double a1 = acos( * tan(theta) - );
        double S1 = Pi - a1 + cos(a1) * sin(a1);
        double ans = S1 / sin(theta);
        printf("%.5f\n", ans);
    }
    return ;
}

H.Guessing the Dice Roll

n个人给出长度为l，互不相同的猜测序列，每次用色子<只有这6个元素：1,2,3,4,5,6>确定添加到旧序列末尾的元素，谁的序列与序列的后缀相同就赢，问每人的胜利概率

直接就是AC自动机上。。。但是到了这一步就不知道如何转成矩阵来高斯消元

后面才发现应该以主串（色子投出的序列）为分配概率的依据而不是以子串（猜测序列）为分配概率的依据

这样就理解了为什么从根出发，概率是1/实边条数，不是1/实边权值和

非根结点转移到下一层时，概率按照正常的1/6来计算，因为到了这步回溯也算在概率里

非叶子结点（就是某人胜利的点）回溯到根的下一层时，要再乘从根出发到对应点的概率

此外数组的第1维是目的点，第2位才是出发点，因为方程式的意义是从不同点一定概率到达本点的总和

#include <bits/stdc++.h>

using namespace std;
typedef double db;
typedef long long ll;
typedef unsigned int uint;
typedef unsigned long long ull;
const db eps=1e-;
const int N=;
const int M=;
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
#define CLR(a, b) memset(a, b, sizeof(a))

struct trie {
    int sz,val[N],fail[N],tr[N][];
    void init() {
        sz=;
        memset(tr,,sizeof(tr));
        memset(val,,sizeof(val));
        memset(fail,,sizeof(fail));
    }
    int trie_insert(int *ch) {
        int w=;
        while (*ch!=-&&tr[w][*ch]) w=tr[w][*ch],ch++;
        while (*ch!=-) tr[w][*ch]=++sz,ch++,w=sz;
        val[w]=;return w;
    }
    void trie_build() {
        queue<int>Q;
        for (int i=;i<;i++)
        if (tr[][i]) Q.push(tr[][i]);
        while (!Q.empty()) {
            int now=Q.front();Q.pop();
            if (val[now]) continue ;
            for (int i=;i<;i++)
            if (tr[now][i]) {
                fail[tr[now][i]]=tr[fail[now]][i];
                Q.push(tr[now][i]);
            } else tr[now][i]=tr[fail[now]][i];
        }
    }
}AC;
double p[N][N];
int gauss(int n) {
    int i,j,k,mxi;
    db h;
    for (i=;i<=n;i++) {
        mxi=i;
        for (j=i;j<=n;j++)
        if (fabs(p[j][i])>fabs(p[mxi][i])) mxi=j;
        if (fabs(p[mxi][i])<eps) return ;
        if (mxi!=i) {
            for (j=i;j<=n+;j++) swap(p[i][j],p[mxi][j]);
        }
        h=p[i][i];
        for (j=i;j<=n+;j++) p[i][j]/=h;
        for (j=;j<=n;j++)
        if (j!=i) {
            h=-p[j][i]/p[i][i];
            for (k=i;k<=n+;k++) p[j][k]+=h*p[i][k];
        }
    }
    return ;
}
int s[];
int ans[];
int main() {
    int t,n,l;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&l);
        AC.init();
        for(int i=;i<n;i++)
        {
            for(int j=;j<l;j++)
            {
                scanf("%d",s+j);s[j]--;
            }
            s[l]=-;
            ans[i]=AC.trie_insert(s);
        }
        AC.trie_build();
        for(int i=;i<=AC.sz;i++)
        {
            s[i]=;
            for(int j=;j<;j++)if(AC.tr[i][j])s[i]++;
        }
        memset(p,,sizeof(p));
        for(int i=;i<=AC.sz;i++)p[i][i]=1.0;
        for(int i=;i<;i++)if(AC.tr[][i])p[AC.tr[][i]][AC.sz+]+=1.0/s[];//从根部出发，由于是按主串算的，要均分
        for(int i=;i<=AC.sz;i++)
        {
            for(int j=;j<;j++)if(AC.tr[i][j])p[AC.tr[i][j]][i]-=1.0/6.0;
            if(s[i]!= && !AC.val[i])//i结点是非叶子且能回溯到边的
            {
                for(int k=;k<;k++)
                {
                    if(AC.tr[][k])p[AC.tr[][k]][i]-=1.0*(-s[i])/6.0/s[];
                }
            }
        }
        gauss(AC.sz);
        for(int i=;i<n;i++)printf("%.6f%c",p[ans[i]][AC.sz+],i==n-?'\n':' ');
    }getchar();getchar();
    return ;
}

I.The Elder

一棵树，从1点到其他点的传递方式有2种：通过其他中转站停留P时再出发，连续赶路，其中连续赶路dis的花费是dis^2，问从1点到其他点的最优距离最长的距离

一开始想到直接树DP，但是还要在树上储存数据不好下手

看了下大神博客才知道有斜率优化这东西

dp[i]=min(dp[j]+(dis[i]-dis[j])^2)+P

然后设j比k优，则

dp[j]+(dis[i]-dis[j])^2+P <= dp[k]+(dis[i]-dis[k])^2+P

得到[(dp[j]+dis[j]*dis[j])-(dp[k]+dis[k]*dis[k])] / 2(dis[j]-dis[k]) <=dis[i].

所以我们可以看出以下两点：我们令g[k,j]=(yj-yk)/(xj-xk)

第一：如果上面的不等式成立，那就说j比k优，而且随着i的增大上述不等式一定是成立的，也就是对i以后算DP值时，j都比k优。那么k就是可以淘汰的。

第二：如果 k<j<i   而且 g[k,j]>g[j,i] 那么 j 是可以淘汰的。

假设  g[j,i]<dis[i]就是i比j优，那么j没有存在的价值

相反如果 g[j,i]>dis[i] 那么同样有 g[k,j]>sum[i]  那么 k比 j优 那么  j 是可以淘汰的

然后就单调队列搞斜率dp

至于树上的回溯导致的状态返回问题，把队尾附近的较优方案取出来标注时间戳还有在队位置，放到栈里，遍历子树时从栈放出来入队

//kopyh
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define MOD 1000000007
//#define N 112345
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N=;
vector<pii> g[N];
int m;
ll dp[N],dist[N];
int tim;
int q[N],head,tail;
struct tripl
{
    int pos,val,timer;
    tripl(){}
    tripl(int pos,int val,int timer){this->pos=pos;this->val=val;this->timer=timer;}
}tmp;
stack<tripl> st;
inline ll dy(int i)
{
    return dp[i]+dist[i]*dist[i];
}

inline ll dx(int j,int k)
{
    return *(dist[j]-dist[k]);
}

inline ll f(int j,int k)
{
    return dy(j)-dy(k);
}
void dfs(int s,int fa)
{
    int curr=tim++;
    while(head<tail && f(q[head+],q[head])<=dist[s]*dx(q[head+],q[head]))head++;
    dp[s]=dp[q[head]]+(dist[s]-dist[q[head]])*(dist[s]-dist[q[head]])+m;
    while(head<tail && f(s,q[tail])*dx(q[tail],q[tail-])<=f(q[tail],q[tail-])*dx(s,q[tail]))
    {
        st.push(tripl(tail,q[tail],curr));
        tail--;
    }
    q[++tail]=s;
    int th=head,tt=tail;
    for(int i=;i<g[s].size();i++)
    {
        int to=g[s][i].first,val=g[s][i].second;
        if(fa==to)continue;
        dist[to]=dist[s]+val;
        head=th,tail=tt;
        while(!st.empty())
        {
            tmp=st.top();
            if(tmp.timer<=curr)break;
            q[tmp.pos]=tmp.val;
            st.pop();
        }
        dfs(to,s);
    }
}

int main()
{
    int i,j,k,cas,T,t,x,y,z,n;
    scanf("%d",&T);
    cas=;
    while(T--)
    {
        ll maxans=;
        scanf("%d%d",&n,&m);
        for(i=;i<=n;i++)g[i].clear();
        for(i=;i<n;i++)
        {
            scanf("%d%d%d",&x,&y,&z);
            g[x].push_back(make_pair(y,z));
            g[y].push_back(make_pair(x,z));
        }
        while(!st.empty())st.pop();
        head=tim=,tail=-;
        dist[]=dist[]=;
        dp[]=-m;
        q[++tail]=;
        int th=head,tt=tail;
        for(i=;i<g[].size();i++)
        {
            int to=g[][i].first,val=g[][i].second;
            dist[to]=dist[]+val;
            head=th,tail=tt;
            while(!st.empty())
            {
                tmp=st.top();
                if(tmp.timer<=)break;
                q[tmp.pos]=tmp.val;
                st.pop();
            }
            dfs(to,);
        }
        for(i=;i<=n;i++)maxans=max(maxans,dp[i]);
        printf("%I64d\n",maxans);
    }
    return ;
}