神经网络入门篇之深层神经网络：详解前向传播和反向传播（Forward and backward propagation）

深层神经网络（Deep L-layer neural network）

复习下前面的内容：

1.逻辑回归，结构如下图左边。一个隐藏层的神经网络，结构下图右边：

注意，神经网络的层数是这么定义的：从左到右，由0开始定义，比如上边右图，\({x}_{1}\)、\({x}_{2}\)、\({x}_{3}\),这层是第0层，这层左边的隐藏层是第1层，由此类推。如下图左边是两个隐藏层的神经网络，右边是5个隐藏层的神经网络。

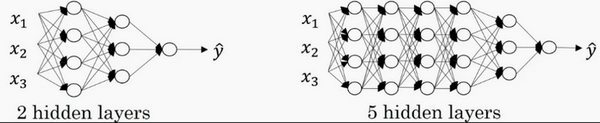
严格上来说逻辑回归也是一个一层的神经网络，而上边右图一个深得多的模型，浅与深仅仅是指一种程度。记住以下要点：

有一个隐藏层的神经网络，就是一个两层神经网络。记住当算神经网络的层数时，不算输入层，只算隐藏层和输出层。

但是在过去的几年中，DLI（深度学习学院 deep learning institute）已经意识到有一些函数，只有非常深的神经网络能学会，而更浅的模型则办不到。尽管对于任何给定的问题很难去提前预测到底需要多深的神经网络，所以先去尝试逻辑回归，尝试一层然后两层隐含层，然后把隐含层的数量看做是另一个可以自由选择大小的超参数，然后再保留交叉验证数据上评估，或者用开发集来评估。

再看下深度学习的符号定义：

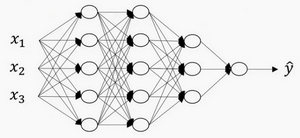
上图是一个四层的神经网络，有三个隐藏层。可以看到，第一层（即左边数过去第二层，因为输入层是第0层）有5个神经元数目，第二层5个，第三层3个。

用L表示层数，上图：\(L=4\)，输入层的索引为“0”，第一个隐藏层\({n}^{[1]}=5\),表示有5个隐藏神经元，同理\({n}^{[2]}=5\)，\({n}^{[3]}=3\)，\({{n}^{[4]}}\)=\({{n}^{[L]}}=1\)（输出单元为1）。而输入层，\({n}^{[0]}={n}_{x}=3\)。

在不同层所拥有的神经元的数目，对于每层l都用\({a}^{[l]}\)来记作l层激活后结果，会在后面看到在正向传播时，最终能会计算出\({{a}^{[l]}}\)。

通过用激活函数 \(g\) 计算\({z}^{[l]}\)，激活函数也被索引为层数\(l\)，然后用\({w}^{[l]}\)来记作在l层计算\({z}^{[l]}\)值的权重。类似的，\({{z}^{[l]}}\)里的方程\({b}^{[l]}\)也一样。

最后总结下符号约定：

输入的特征记作\(x\)，但是\(x\)同样也是0层的激活函数，所以\(x={a}^{[0]}\)。

最后一层的激活函数，所以\({a}^{[L]}\)是等于这个神经网络所预测的输出结果。

前向传播和反向传播

• 之前的神经网络入门篇都是基于浅层神经网络进行的，此篇开始基于深层神经网络进行

之前学习了构成深度神经网络的基本模块，比如每一层都有前向传播步骤以及一个相反的反向传播步骤，这次讲讲如何实现这些步骤。

先讲前向传播，输入\({a}^{[l-1]}\)，输出是\({a}^{[l]}\)，缓存为\({z}^{[l]}\)；从实现的角度来说可以缓存下\({w}^{[l]}\)和\({b}^{[l]}\)，这样更容易在不同的环节中调用函数。

所以前向传播的步骤可以写成： \({z}^{[l]}={W}^{[l]}\cdot{a}^{[l-1]}+{b}^{[l]}\)

​ \({{a}^{[l]}}={{g}^{[l]}}\left( {{z}^{[l]}}\right)\)

向量化实现过程可以写成： \({z}^{[l]}={W}^{[l]}\cdot {A}^{[l-1]}+{b}^{[l]}\)

​ \({A}^{[l]}={g}^{[l]}({Z}^{[l]})\)

前向传播需要喂入\({A}^{[0]}\)也就是\(X\)，来初始化；初始化的是第一层的输入值。\({a}^{[0]}\)对应于一个训练样本的输入特征，而\({{A}^{[0]}}\)对应于一整个训练样本的输入特征，所以这就是这条链的第一个前向函数的输入，重复这个步骤就可以从左到右计算前向传播。

下面讲反向传播的步骤：

输入为\({{da}^{[l]}}\)，输出为\({{da}^{[l-1]}}\)，\({{dw}^{[l]}}\), \({{db}^{[l]}}\)

所以反向传播的步骤可以写成：

（1）\(d{{z}^{[l]}}=d{{a}^{[l]}}*{{g}^{[l]}}'( {{z}^{[l]}})\)

（2）\(d{{w}^{[l]}}=d{{z}^{[l]}}\cdot{{a}^{[l-1]}}~\)

（3）\(d{{b}^{[l]}}=d{{z}^{[l]}}~~\)

（4）\(d{{a}^{[l-1]}}={{w}^{\left[ l \right]T}}\cdot {{dz}^{[l]}}\)

（5）\(d{{z}^{[l]}}={{w}^{[l+1]T}}d{{z}^{[l+1]}}\cdot \text{ }{{g}^{[l]}}'( {{z}^{[l]}})~\)

式子（5）由式子（4）带入式子（1）得到，前四个式子就可实现反向函数。

向量化实现过程可以写成：

（6）\(d{{Z}^{[l]}}=d{{A}^{[l]}}*{{g}^{\left[ l \right]}}'\left({{Z}^{[l]}} \right)~~\)

（7）\(d{{W}^{[l]}}=\frac{1}{m}\text{}d{{Z}^{[l]}}\cdot {{A}^{\left[ l-1 \right]T}}\)

（8）\(d{{b}^{[l]}}=\frac{1}{m}\text{ }np.sum(d{{z}^{[l]}},axis=1,keepdims=True)\)

（9）\(d{{A}^{[l-1]}}={{W}^{\left[ l \right]T}}.d{{Z}^{[l]}}\)

总结一下：

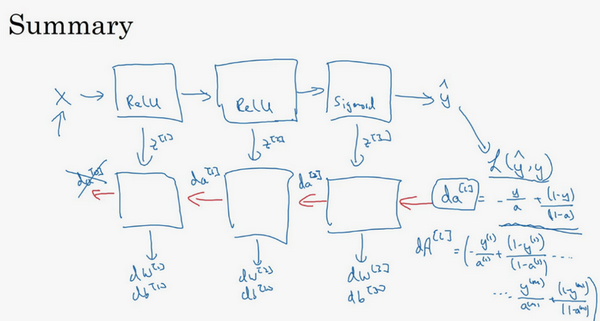
第一层可能有一个ReLU激活函数，第二层为另一个ReLU激活函数，第三层可能是sigmoid函数（如果做二分类的话），输出值为，用来计算损失；这样就可以向后迭代进行反向传播求导来求\({{dw}^{[3]}}\)，\({{db}^{[3]}}\) ，\({{dw}^{[2]}}\) ，\({{db}^{[2]}}\) ，\({{dw}^{[1]}}\) ，\({{db}^{[1]}}\)。在计算的时候，缓存会把\({{z}^{[1]}}\) \({{z}^{[2]}}\)\({{z}^{[3]}}\)传递过来，然后回传\({{da}^{[2]}}\)，\({{da}^{[1]}}\) ，可以用来计算\({{da}^{[0]}}\)，但不会使用它，这里讲述了一个三层网络的前向和反向传播，还有一个细节没讲就是前向递归——用输入数据来初始化，那么反向递归（使用Logistic回归做二分类）——对\({{A}^{[l]}}\) 求导。

忠告：补补微积分和线性代数，多推导，多实践。