Codeforces(1500板刷)

目录

• 写在前面
• 1. A. Did We Get Everything Covered?(构造、思维)
  • 题目链接
  • 题意
  • 题解
  • 代码
  • 总结
• 2 F. Greetings（离散化+树状数组）
  • 题目链接
  • 题意
  • 题解
  • 代码
  • 总结
• 3. B. Milena and Admirer（贪心、小结论、思维）
  • 题目链接
  • 题意
  • 题解
  • 代码
  • 总结
• 4. C. Smilo and Monsters（贪心、典题、结论）
  • 题目链接
  • 题意
  • 题解
  • 代码
  • 总结
• 5. D. In Love(贪心)
  • 题目链接
  • 题意
  • 题解
  • 代码
  • 总结
• 6. C. Card Game(思维、找性质)
  • 题目链接
  • 题面
  • 题解
  • 代码
  • 总结
• 7 E. Block Sequence
  • 链接
  • 题意
  • 题解
  • 代码
  • 总结
• 8 B. Effects of Anti Pimples（调和级数、埃式筛思想）
  • 题目链接
  • 题面
  • 题解
  • 代码
  • 总结
• 9 G. ABBC or BACB(思维、找规律、找性质)
  • 链接
  • 题面
  • 题解
  • 代码
  • 总结
• 10 E. Data Structures Fan（异或性质、前缀和思想）
  • 链接
  • 题面
  • 题解
  • 代码
  • 总结

---

写在前面

开始板刷1500了，主要是最近卡1300-1400上不去，发现cf很多思维题要不是想不到，要不就是签的慢，被读题卡了心态就巨难受，一下就不想写了，而且现在学知识点容易陷入递归，学到一个知识点发现需要用其他知识点，然后又去学其他知识点，然后学完还需要对这些一堆知识点做题练习不然只会板子根本没有什么对算法深刻的理解。感觉不如这样去板刷，遇到不会的只学这个不去学太多，在题目中理解知识点应该比单纯泛泛去学可能效果会更好。也记录一下，自己1500刷多少，才能有提升。

1. A. Did We Get Everything Covered?(构造、思维)

题目链接

---

A. Did We Get Everything Covered?

---

题意

---

给\(n，k\)以及长度为\(m\)的一个小写的字符串。

字符串的子序列是否包含用前\(k\)个小写字母构成的长度为n的字符串的所有情况

---

题解

1. 首先判断有没有解：
   
   要构成所有的字符串，我们可以把原串进行拆分，拆分成n个段，每段如果都包含前k个小写字母至少一次，则说明有解，反之说明无解。
2. 无解的情况下，考虑如何构造答案。
   
   用每一段最后一次出现的字符，加上不满足的段中没有出现的字符
   
   正确性？每一段最后出现的字符一定在前面没出现过，只能在后面出现，这样构造出来的子序列是正确的

代码

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back

using namespace std;
const int mod=998244353;
void solve() {
	int n,k,m;
	string s;
	cin>>n>>k>>m;
	cin>>s;
	set<char>cnt;
	int cur=0;
	string ans;
	rep(i,0,m-1) {
		cnt.insert(s[i]);
		if(cnt.size()==k) {
			ans+=s[i];
			++cur;
			cnt.clear();
		}
		if(cur>=n) {
			cout<<"YES"<<endl;
			return;
		}
	}
	cout<<"NO"<<endl;
	int len=ans.size();
	rep(i,0,k-1) {
		char c='a'+i;
		if(cnt.count(c)==0) {
			rep(j,1,n-len)	ans+=c;
			break;
		}
	}
	cout<<ans<<endl;
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
//	freopen("1.in", "r", stdin);
	int _;
	cin>>_;
	while(_--)
		solve();
	return 0;
}

总结

有判定正确性的思路，但是不会构造

wa了几发。最开始是构造的思路是错的

后面有一个小细节处理的不好，当要修改\(string\)时，就不能用\(string\)的\(size\)作为循环的控制条件，这样很容易寄。

很好的一道构造题目

---

2 F. Greetings（离散化+树状数组）

题目链接

F. Greetings

题意

题解

由于两个人的速度是一样的，所以到达终点之前两个人是不会相遇的，考虑一下什么情况两个人会相遇，其中一个人到达终点时，另一个人，终点所在地的前面，并且它的终点在更右边。

将两个人的起点终点分别用\(S_a 、S_b、 E_a、 E_b\)表示，并假设\(a\)在前\(b\)在后（b在前是对称的），有下图

1. \(a\)的终点\(<\) \(b\)的终点，这时两者同时出发，a到终点时，b已经经过的a的终点，两者不会相遇，对答案没有贡献
   
   
2. \(a\)的终点\(>\) \(b\)的终点，这时b会先到终点，速度一样，a此时还没有到达\(E_b\)，此时两者一定会在\(E_b\)相遇
   
   
   
   所以答案转化为对于当前区间计算有多少个区间被它所包含。

因为这道题目数据的实际大小是没有意义的，相对大小是有用的，并且值域比较大，我们考虑离散化，然后通过树状数组去查询。

具体的做法是，先按右端点从小打大排序，然后从前往后遍历区间，每次查询起点大于当前点起点的个数。就是这个区间对答案产生的贡献。

代码

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back

using namespace std;

void solve() {
	int n;
	cin>>n;
	struct node{
		int l,r;
		bool operator<(const node &t)const{
			return r<t.r;
		}
	};
	vector<node>a(n);
	vector<int>b(2*n);
	int k=0;
	rep(i,0,n-1){
		cin>>a[i].l>>a[i].r;
		b[k++]=a[i].l;
		b[k++]=a[i].r;
	}
	sort(b.begin(),b.end());
	rep(i,0,n-1){
		a[i].l=lower_bound(b.begin(),b.end(),a[i].l)-b.begin()+1;
		a[i].r=lower_bound(b.begin(),b.end(),a[i].r)-b.begin()+1;
	}
	sort(a.begin(),a.end());
//	rep(i,0,n-1){
//		cout<<a[i].l<<' '<<a[i].r<<endl;
//	}
	vector<int>c(2*n+1,0);
	auto lowbit=[](int x){
		return x&-x;
	};

	auto add=[&](int x,int k)->void{
		for(int i=x;i<=2*n;i+=lowbit(i)){
			c[i]+=k;
		}
	};

	auto sum=[&](int x){
		int res=0;
		for(int i=x;i;i-=lowbit(i)){
			res+=c[i];
		}
		return res;
	};
	int ans=0;
	rep(i,0,n-1){
		int r=a[i].r,l=a[i].l;
		ans+=sum(r)-sum(l-1);
		add(l,1);
	}
	cout<<ans<<endl;
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
//	freopen("1.in", "r", stdin);
	int _;
	cin>>_;
	while(_--)
		solve();
	return 0;
}

---

总结

1. 离散化的板子记得不是很熟，这种东西应该很熟并且默写的很快的
2. 树状数组用的还是比较少有些细节记得不太清，就比如树状数组的下标是从几开始的？
   
   答案是1，这就导致离散化的时候也要从1开始。
3. 看了一些题解，发现了这类问题被称为二维偏序问题
   
   \(a_i<a_j、b_i>b_j\)

---

3. B. Milena and Admirer（贪心、小结论、思维）

题目链接

B. Milena and Admirer

题意

给一个长度为\(n\)的序列，我们通过操作使这个序列变成非递减序列

操作：对\(a[i]\)，我们将\(a[i]\)删除，将\(a[i]-x、x\)插入原位置，要求\(x<a[i]\)

求最小的操作次数

题解

考虑贪心

对于满足\(a[i]<=a[i+1]\)的\(i\)我们不去操作

对于不满足条件的\(i\)，我们考虑将\(a[i]\)拆成k个满足条件并且尽可能大的数。（这里k最多为\(a[i]-1\)因为一个数最多全部拆成1）。

考虑如何拆才能使答案最优，我们希望当前拆完的数尽可能大，在满足拆完的所有数都小于\(a[i+1]\)的情况下。，因为我们当前拆完的数的最小值会影响前面的数的拆分，我们肯定是希望拆完之后最小值最大的，如何才能达到最小值最大呢？

考虑去平均拆。

对于\(a[i+1]>a[i]\)需要将拆\(cnt=a[i]/a[i+1]+(a[i]%a[i+1]!=0)\)成这么多个数，需要拆

\(cnt-1\)次，还需要去维护一个最小值\(a[i]/cnt\)，从后往前扫一遍维护最小值，统计答案即可。

代码

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back

using namespace std;

void solve() {
	int n;
	cin>>n;
	vector<int>a(n+1);
	rep(i,1,n) {
		cin>>a[i];
	}
	int cur=1e9;
	int ans=0;
	//倒着枚举一遍
	fep(i,n,1) {
		if(a[i]<cur){
			cur=a[i];
		}else if(a[i]%cur==0){
			ans+=a[i]/cur-1;
		}else{
			int cnt=a[i]/cur+1;
			ans+=(cnt-1);
			cur=a[i]/cnt;
		}
	}
	cout<<ans<<endl;
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
//	freopen("1.in", "r", stdin);
	int _;
	cin>>_;
	while(_--)
		solve();
	return 0;
}

总结

这道题目主要是要想清楚对于一个数如何拆分才能对后面的影响最小。

---

4. C. Smilo and Monsters（贪心、典题、结论）

题目链接

题意

题解

代码

总结

---

5. D. In Love(贪心)

题目链接

D. In Love

题意

线段的集合，有两种操作

1. 插入一个线段
2. 删除一个线段
   
   每次操作后都要去查询是否存在两个线段不相交

题解

首先先看两个线段不相交需要满足什么条件



也就是较\(大l>小r\)即可满足不相交

我们进行推广

当集合中，最大的\(l>\)最小的\(r\)时就存在区间不相交

注意是严格大于。

这样我们只需要维护两个集合，左端点的集合和右端点的集合，然后每次查询集合中的最值。

\(set\)和\(multiset\)都可以完成这件事，这道题目里面区间可能重复，所以用\(multiset\)去维护最大值最小值即可。

代码

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back

using namespace std;

void solve() {
	int q;
	cin>>q;

	multiset<int>sl,sr;
	while(q--){
		char op;
		cin>>op;
		int l,r;
		cin>>l>>r;
		if(op=='+'){
			sl.insert(l);
			sr.insert(r);
		}else{
			sl.erase(sl.find(l));
			sr.erase(sr.find(r));
		}
		if(sl.size()<=1||sr.size()<=1){
			cout<<"NO"<<endl;
			continue;
		}
		int d=(*sl.rbegin())-(*sr.begin());
		if(d>0){
			cout<<"YES"<<endl;
		}else{
			cout<<"NO"<<endl;
		}
	}
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
//	freopen("1.in", "r", stdin);
	int _;
//	cin>>_;
//	while(_--)
	solve();
	return 0;
}

总结

1. 区间不相交的充要条件
2. multiset的erase用法
   
   不小心就用错了，erase可以传入迭代器的位置，也可以传入要删除的值，如果在set里面这两个都可以，在multiset里面一个值可能出现多次，如果传入值，就会把这所有数都删除，如果只想删除一个，可以先用find函数得到一个迭代器的位置再删除

---

6. C. Card Game(思维、找性质)

题目链接

C. Card Game

题面

题解

代码

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back

using namespace std;

void solve() {
	int n;
	cin>>n;
	vector<int>a(n+1);
	rep(i,1,n){
		cin>>a[i];
	}
	int ans=0;
	if(n==1){
		if(a[1]>0){
			cout<<a[1]<<endl;
		}else{
			cout<<0<<endl;
		}
		return;
	}else {
		if(a[1]>0){
			ans+=a[1];
			if(a[2]>0){
				ans+=a[2];
			}
		}else{
			ans=max(0*1ll,a[1]+a[2]);
		}
		rep(i,3,n){
			if(a[i]>0)	ans+=a[i];
		}
	}
	cout<<ans<<endl;
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
//	freopen("1.in", "r", stdin);
	int _;
	cin>>_;
	while(_--)
	solve();
	return 0;
}

总结

7 E. Block Sequence

链接

E. Block Sequence

题意

一个数组删除最少的数使数组变为美丽的

美丽的定义：

第一个数是长度看，后面k是k个数。

题解

考虑dp

\(f[i]\)表示将从i到n的所有数都变成美丽的花费最小

转移

\(f[i]=min(f[i+1]+1,f[i+a[i]+1]);\)

初始化：

\(f[n]=1;\)

\(f[n+1]=0\):这里表示一个都不删从第一个到第n个恰好是美丽的

这个是从后往前推，所以是倒序循环。

答案就是\(f[1]\)

代码

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back

using namespace std;

void solve() {
	int n;
	cin>>n;
	vector<int>a(n+2);
	rep(i,1,n){
		cin>>a[i];
	}
	vector<int>f(n+2);
	f[n]=1;
	f[n+1]=0;
	fep(i,n-1,1){
		f[i]=f[i+1]+1;
		if(i+a[i]<=n){
			f[i]=min(f[i],f[i+a[i]+1]);
		}
	}
	cout<<f[1]<<endl;
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
//	freopen("1.in", "r", stdin);
	int _;
	cin>>_;
	while(_--)
	solve();
	return 0;
}

总结

非常不错的一道dp题目。

给自己的启发是dp的顺序不止能从前往后，也可以逆序，只要初始化好状态。

---

8 B. Effects of Anti Pimples（调和级数、埃式筛思想）

题目链接

B. Effects of Anti Pimples

题面

题解

对于每个数，如果它被选上，那么所有它的倍数都会被选上，我们关心的是这些数中的最大值，可以类似线性筛一样，把每个数都变成这个最大值，然后对于计算每个数对于答案的贡献，问题就转化成了，所有子序列的最大值的和。

这个问题我们可以通过排序+快速幂解决。

代码

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back
#define vi vector<int>

using namespace std;
const int mod=998244353;

int ksm(int a,int b,int p){
	int res=1;
	while(b){
		if(b&1){
			res=res*a%p;
		}
		a=a*a%p;
		b>>=1;
	}
	return res;
}

void solve() {
	int n;
	cin>>n;
	vi a(n+1);
	rep(i,1,n){
		cin>>a[i];
	}
	rep(i,1,n){
		for(int j=i+i;j<=n;j+=i){
			a[i]=max(a[i],a[j]);
		}
	}
	sort(a.begin()+1,a.end());
	int ans=0;
	rep(i,1,n){
		ans=(ans+a[i]*ksm(2,i-1,mod)%mod)%mod;
	}
	cout<<ans<<endl;
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
//	freopen("1.in", "r", stdin);
	int _;
//	cin>>_;
//	while(_--)
	solve();
	return 0;
}

总结

1. 快速幂这些东西经常用的不能写错
2. 这种倍数，会很容易和筛法结合，很重要的思想。

---

9 G. ABBC or BACB(思维、找规律、找性质)

链接

G. ABBC or BACB

题面

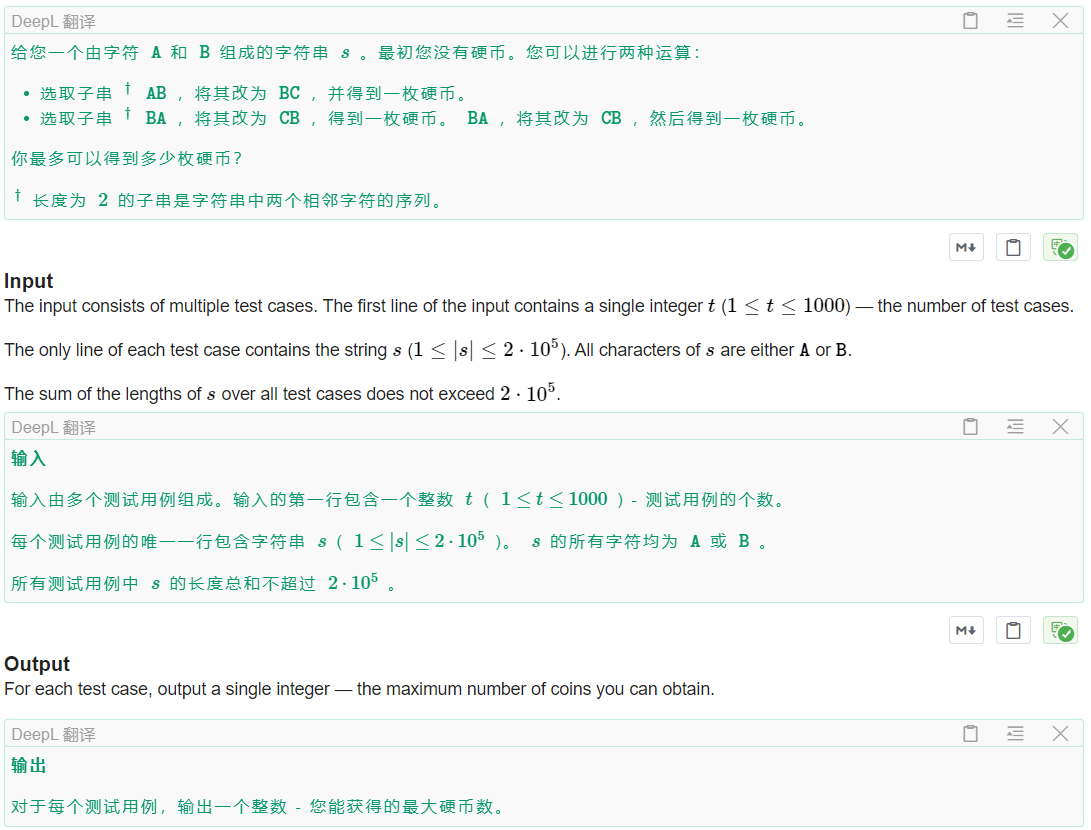
题解

代码

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back
#define vi vector<int>

using namespace std;

void solve() {
	string s;
	cin>>s;
	int num=0,sum=0;
	vi a;
	rep(i,0,s.size()-1){
		if(s[i]=='A'){
			num++;
		}else{
			a.pb(num);
			num=0;
		}
	}
	a.pb(num);
	sum=accumulate(a.begin(),a.end(),0);
	cout<<sum-*min_element(a.begin(),a.end())<<endl;
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
//	freopen("1.in", "r", stdin);
	int _;
	cin>>_;
	while(_--)
	solve();
	return 0;
}

总结

1. 性质很重要
2. 多手模几个样例
   
   学到了两个stl中的算法
3. accumulate(a.begin(),a.end(),0):时间复杂度是\(O(n)\)的
4. min_element(a.begin(),a.end())：返回的是迭代器。

---

10 E. Data Structures Fan（异或性质、前缀和思想）

链接

E. Data Structures Fan

题面

题解

异或的性质。

当异或遇到区间。

考虑用前缀和的思想解决。

这里分开处理0和1，因为最后我们要查询的是所有1和0位置处的\(a[i]\)的异或

我们考虑修改一段区间对于0、1的影响，我们希望将一段区间内的0处变成1，1变成0

然后假设我们现在这一段区间是\([3，8]\)

0:a[3] ^ a[5] ^ a[6]

1:a[4] ^ a[7] ^ a[8]

要使两者交换就需要异或上a[3] ^ a[4] ^ a[5] ^ a[6] ^ a[7] ^ a[8]，也就是这个区间内所有数的异或

代码

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back
#define vi vector<int>

using namespace std;

void solve() {
	int n;
	cin>>n;
	vector<int>a(n+1);
	vector<int>sum(n+1);
	rep(i,1,n){
		cin>>a[i];
		sum[i]=sum[i-1]^a[i];
	}
	string s;
	cin>>s;
	vector<int>ans(2);
	rep(i,0,s.size()-1){
		if(s[i]=='0')	ans[0]^=a[i+1];
		else	ans[1]^=a[i+1];
	}
	int q;
	cin>>q;
	while(q--){
		int op;
		cin>>op;
		if(op==1){
			int l,r;
			cin>>l>>r;
			ans[0]^=(sum[r]^sum[l-1]);
			ans[1]^=(sum[r]^sum[l-1]);
		}else{
			int d;
			cin>>d;
			cout<<ans[d]<<' ';
		}
	}
	cout<<endl;
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
//	freopen("1.in", "r", stdin);
	int _;
	cin>>_;
	while(_--)
	solve();
	return 0;
}

总结

1. 所有逆运算的都可以通过前缀和思想来进行处理
   • 加减
   • 乘除
   • 异或、异或