题解 P1884 【[USACO12FEB]过度种植（银）Overplanting 】

什么,扫描线需要线段树?

那我第一个不干啊(其实是不会写)

这里介绍一种裸的扫描线:

我们根据x排序,对于相等的 \(x\) ,将 \(y\) 进入和退出分类讨论,然后全部放进set里面.每次 \(x\) 不相等的时候,答案就是 (现在y覆盖的乘以(现在的x-以前的x))

具体的判断方法:

1.y的判断:

将每个长方形的上方点记做出口,下方点记做入口.用一个set记录在某区间内所有的 \(y\) 值.每次从下往上扫,如果某个y是入口就将 \(sz\) +1,否则就将 \(sz\) -1.如果 \(sz\)==0 的时候就将你整个区间的值加到re里面

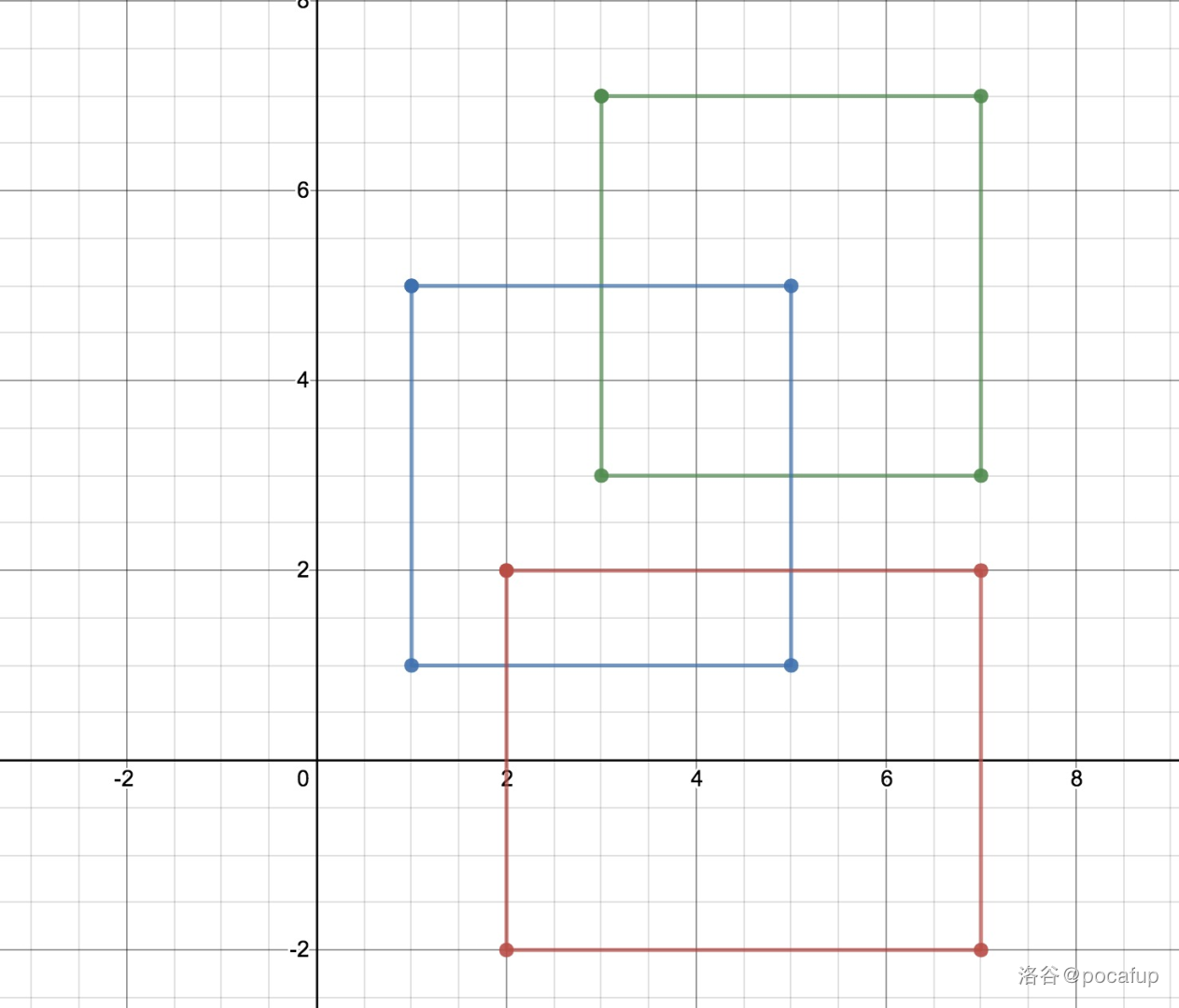
如图,每次x变的时候只需要保存中间y的值,然后用移动的x乘y就好了

注:我保存y进入和退出状态的原因就是为了记录中间是否有空位.可以发现,如果中间有空位,那么证明所有进入的点已经退出了,所以那一段不需要加上去(不懂可以画一下图)

long long query_up(){
  long long re = 0,prev = -1,sz = 0;
  for (multiset<pair<long long,bool> >::iterator i=se.begin();i!=se.end();++i){
    pair<long long,bool> now = *i;
    if (sz==0) {prev = now.f;sz++;}
    else if (now.s) sz++;
    else sz--;
    if (sz==0) re+=(now.f-prev);//如果现在所以的y都已经出去了,那么答案就是最后一个y的出口-第一个y的入口
  }
  return re;
}

想到了这点以后这题的难点基本上就解决了.

因为有负数,我将每个数都加上了1e8,这样就可以完全不管负数了

不开long long见祖宗

完整代码:

#include <iostream>
#include <set>
#include <algorithm>
#include <iterator>
#include <utility>
using namespace std;
const long long MAXN = 1e5+5;
#define pp pair<long long,long long>
#define f first
#define s second
long long n,ans = 0;
multiset<pair<long long,bool> > se;
struct Edge{
  long long x,y; bool in,in2;
}edge[MAXN*4];
Edge add_edge(long long a, long long b, bool bo,bool bo2){
  Edge tmp;
  tmp.x = a;
  tmp.y = b;
  tmp.in = bo;
  tmp.in2 = bo2;
  return tmp;
}
bool sorted(Edge a, Edge b){
  return a.x<b.x;
}
long long query_up(){
  long long re = 0,prev = -1,sz = 0;
  for (multiset<pair<long long,bool> >::iterator i=se.begin();i!=se.end();++i){
    pair<long long,bool> now = *i;
    if (sz==0) {prev = now.f;sz++;}
    else if (now.s) sz++;
    else sz--;
    if (sz==0) re+=(now.f-prev);
  }
  return re;
}
int main(){
  cin >> n;
  for (long long i=0;i<n;i++){
    long long a,b,c,d; cin >> a >>b >> c >> d;
    a+=1e8;b+=1e8;c+=1e8;d+=1e8;
    edge[4*i] = add_edge(a,b,1,0);
    edge[4*i+1] = add_edge(a,d,1,1);
    edge[4*i+2] = add_edge(c,b,0,0);
    edge[4*i+3] = add_edge(c,d,0,1);
    //两种状态,第一种表示x变不变,第二种表示y变不变
  }
  sort(edge,edge+4*n,sorted);
  long long prev = 0;
  for (long long i=0;i<4*n;i++){
    if (edge[i].x!=prev){//如果x变了
      if (se.size()) ans += (edge[i].x-prev)*query_up();
      prev = edge[i].x;
    }
    if (edge[i].in==1) se.insert(make_pair(edge[i].y,edge[i].in2));//如果这点是进入的点,就将y加入set
    else se.erase(se.find(make_pair(edge[i].y,edge[i].in2)));
//否则将y扔出set
  }
  cout << ans;
}

留一组测试数据造福后人

3
3 7 7 3
1 5 5 1
2 2 7 -2

答案45