poj 1523 SPF【点双连通求去掉割点后bcc个数】

SPF

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 7246		Accepted: 3302

Description

Consider the two networks shown below. Assuming that data moves around these networks only between directly connected nodes on a peer-to-peer basis, a failure of a single node, 3, in the network on the left would prevent some of the still available nodes from communicating with each other. Nodes 1 and 2 could still communicate with each other as could nodes 4 and 5, but communication between any other pairs of nodes would no longer be possible.

Node 3 is therefore a Single Point of Failure (SPF) for this network. Strictly, an SPF will be defined as any node that, if unavailable, would prevent at least one pair of available nodes from being able to communicate on what was previously a fully connected network. Note that the network on the right has no such node; there is no SPF in the network. At least two machines must fail before there are any pairs of available nodes which cannot communicate.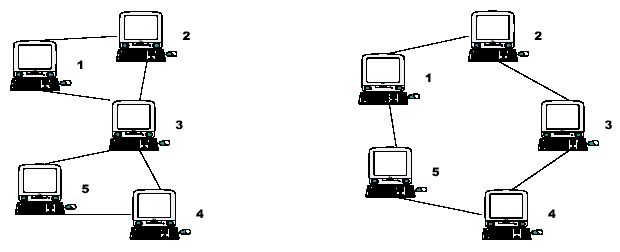 

Input

The input will contain the description of several networks. A network description will consist of pairs of integers, one pair per line, that identify connected nodes. Ordering of the pairs is irrelevant; 1 2 and 2 1 specify the same connection. All node numbers will range from 1 to 1000. A line containing a single zero ends the list of connected nodes. An empty network description flags the end of the input. Blank lines in the input file should be ignored.

Output

For each network in the input, you will output its number in the file, followed by a list of any SPF nodes that exist.

The first network in the file should be identified as "Network #1", the second as "Network #2", etc. For each SPF node, output a line, formatted as shown in the examples below, that identifies the node and the number of fully connected subnets that remain when that node fails. If the network has no SPF nodes, simply output the text "No SPF nodes" instead of a list of SPF nodes.

Sample Input

1 2
5 4
3 1
3 2
3 4
3 5
0

1 2
2 3
3 4
4 5
5 1
0

1 2
2 3
3 4
4 6
6 3
2 5
5 1
0

0

Sample Output

Network #1
  SPF node 3 leaves 2 subnets

Network #2
  No SPF nodes

Network #3
  SPF node 2 leaves 2 subnets
  SPF node 3 leaves 2 subnets

题意：求去掉割点之后 整个图分为多少个bcc  输出割点的编号以及去掉割点后bcc个数

割点：如果在无向图G中去掉一个顶点(自然同时去掉与该顶点相关联的所有边)后图的连通分支数增加，则称该顶点为G的割点

节点是割点的条件满足1或者2：
1、节点是根节点并且这个根节点有两个以及两个以上的子节点
2、节点不是根节点 满足dfn[u]<=low[v];

去掉割点后bcc增加的数目：
1：如果割点是根节点它的子节点数目为son去掉之后bcc增加son个
2：割点不是根节点它的子节点数目为son个去掉之后 bcc增加son+1个

#include<stdio.h>
#include<string.h>
#include<stack>
#include<algorithm>
#define MAX 2100
#define INF 0x7fffff
using namespace std;
int dfn[MAX],low[MAX];
int dfsclock,ebccnt;
int addbcc[MAX];//记录去掉割点后bcc个数
int head[MAX],ans;
int iscut[MAX];//记录是否是割点
struct node
{
	int beg,end,next;
}edge[MAX];
void init()
{
    ans=0;
	memset(head,-1,sizeof(head));
}
void add(int u,int v)
{
	edge[ans].beg=u;
	edge[ans].end=v;
	edge[ans].next=head[u];
	head[u]=ans++;
}
void tarjan(int u,int fa)
{
	int i,v;
	dfn[u]=low[u]=++dfsclock;
	int son=0;//记录子节点数目
	for(i=head[u];i!=-1;i=edge[i].next)
	{
		v=edge[i].end;
		if(!dfn[v])
		{
			son++;
			tarjan(v,u);
			low[u]=min(low[u],low[v]);
			if(dfn[u]<=low[v])//是割点，先不考虑是不是根节点
			{
				addbcc[u]++;//这是割点的一个子节点，bcc数目加1
				iscut[u]=1;
			}
		}
		else
		    low[u]=min(dfn[v],low[u]);
	}
	if(fa<0&&son<2)//不是根节点
	{
		iscut[u]=0;
		addbcc[u]=0;
	}
	if(fa<0&&son>1)//是根节点
	{
		iscut[u]=1;
		addbcc[u]=son-1;//这里当是根节点时去掉割点bcc数目为子节点数目son
		         //但是因为上边我们for循环中求bcc时全部当做非根节点求这样
				 //其非根节点割点去掉之后bcc个数 为son+1，为了最后输出时统一加1
				 //这里我们让 addbcc[u]=son-1;
	}
}
void find(int l,int r)
{
	dfsclock=0;
	memset(low,0,sizeof(low));
	memset(dfn,0,sizeof(dfn));
	memset(addbcc,0,sizeof(addbcc));
	memset(iscut,0,sizeof(iscut));
	for(int i=l;i<=r;i++)
	{
		if(!dfn[i])
		    tarjan(i,-1);
	}
}
int main()
{
	int n,m,j,i,a,b;
	int Max,Min;
	int k=0;
	while(1)
	{
		int t=0;
		Max=-1;Min=INF;
		init();
		while(scanf("%d",&a)&&a!=0)
		{
			t++;
			scanf("%d",&b);
			Max=max(Max,max(a,b));
			Min=min(Min,min(a,b));
			add(a,b);
			add(b,a);
		}
		if(a==0&&t==0)
		    break;
		find(Min,Max);
		int flag=0;
		printf("Network #%d\n",++k);
		for(i=Min;i<Max;i++)
		{
			if(iscut[i])
			{
				flag=1;
				printf("  SPF node %d leaves %d subnets\n",i,addbcc[i]+1);
			}
		}
		if(!flag)
		    printf("  No SPF nodes\n");
		printf("\n");
	}
	return 0;
}