GiftWrapping算法解决二维凸包问题

一.问题描述

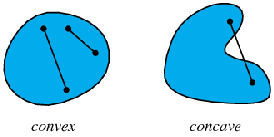
凸集(Convex Set): 任意两点的连线都在这个集合内的集合就是一个凸集.
            ⒈对于一个集合D，D中任意有限个点的线性组合的全体称为D的凸包。
            ⒉对于一个集合D，所有包含D的凸集之交称为D的凸包(由此定义可以想到分治算法)。
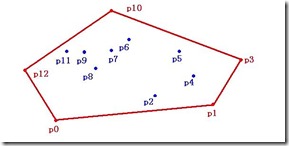
        可以证明，上述两种定义是等价的。点集Q的凸包（convex hull）是指一个最小凸多边形，满足Q中的点或者在多边形边上或者在其内。下图中由红色线段表示的多边形就是点集Q={p0,p1,...p12}的凸包。一组平面上的点，求一个包含所有点的最小的凸多边形，这就是凸包问题了，这可以形象地想象成在地上放置一些不可移动的木桩，用一根绳子把他们尽量紧地圈起来，并且为凸边形，这就是凸包了。

二.GiftWrapping算法

又叫卷包裹算法，复杂度O(n*h)，n表示共几个点，h表示极点个数。

• 理论准备

向量叉积：也被称为矢量积、叉积（即交叉乘积）、外积，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个伪向量而不是一个标量，并且两个向量的叉积与这两个向量垂直，方向由右手法则确定。两个向量a和b的叉积写作a×b（有时也被写成a∧b，避免和字母x混淆）。
a×b=(aybz-azby)i+(azbx-axbz)j+(axby-aybx)k,为了帮助记忆，利用三阶行列式，写成
|  i    j   k|
|ax ay az|
|bx by bz|。
        b×a= -a×b，三角形ABC的面积=1/2*abs(AB×AC)(这个公式可以解决一些精度问题)，不满足结合律，但满足雅可比恒等式：a× (b×c) +b× (c×a) +c× (a×b) =0和拉格朗日公式a× (b×c) =b(a·c) -c(a·b),可以简单地记成“BAC - CAB”。这个公式在物理上简化向量运算非常有效，需要注意的是，这个公式对微分算子不成立。

• 算法描述

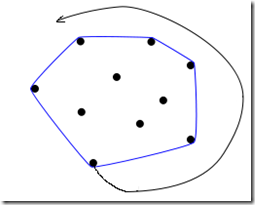
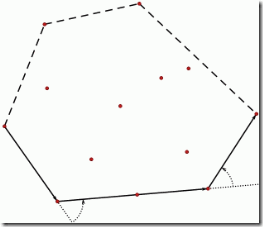
卷包裹算法从一个必然在凸包上的点开始向着一个方向依次选择最外侧的点，当回到最初的点时，所选出的点集就是所要求的凸包。这里还有两个问题不是很清楚:
        1.怎么确定一个肯定在凸包上的点?
        这个问题很好解决，取一个最左边的也就是横坐标最小的点（或最下边的点，纵坐标最小的），如果有多个这样的点， 就取这些点里纵坐标（横坐标）最小的，这样可以很好的处理共线的情况。
        2.如何确定下一个点(即最外侧的点)?

向量的叉积是不满足交换律的，向量A乘以向量B， 如果为正则为A逆时针旋转向B，否则为顺时针，当然这里A转向B的角总是考虑一个小于180度以内的角。

三.算法的Java实现

看完这段代码，直接把POJ1113AC了吧。

import java.util.*;
 
class Point implements Comparable {
    double x;
    double y;
 
    public int compareTo(Object o) {// 按x升序排列,x相同按y升序
        Point b = (Point) o;
 
        if (this.x > b.x)
            return 1;
        else if (this.x == b.x) {
            if (this.y > b.y)
                return 1;
            else if (this.y == b.y)
                return 0;
            else
                return -1;
        } else
            return -1;
    }
}
 
public class GiftWrap {
 
    Point[] point;// 已知的平面上的点集
    boolean[] vis;// 标pointA[i]是否已在凸包中
    Queue<Integer> queue = new LinkedList<Integer>();// 点集的凸包,
 
    int n;
    int l;
 
    public GiftWrap() {
 
    }
 
    // 向量ca与ba的叉积
    double cross(Point c, Point a, Point b) {
        return (c.x - a.x) * (a.y - b.y) - (c.y - a.y) * (a.x - b.x);
    }
 
    // 求距离,主要是为了求极点
    public double distance(Point p1, Point p2) {
        return (Math.hypot((p1.x - p2.x), (p1.y - p2.y)));
    }
 
    public void go() {
 
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        point = new Point[n + 1];
        vis = new boolean[n + 1];
        for (int i = 1; i <= n; i++) {// 输入从1开始
            point[i] = new Point();
            point[i].x = sc.nextDouble();
            point[i].y = sc.nextDouble();
        }
        Arrays.sort(point, 1, point.length - 1);// 注意这个排序从1开始
        // 确定一个肯定在凸包上的点
        vis[1] = true;// 注意这里将point[1]标记为放进凸包,不过并没有真的放入队列
        int in = 1;//在凸包上的点
 
        while (true) {
            int not = -1;
            for (int i = 1; i <= n; i++) {
                if (!vis[i]) {// 找一个不在凸包上的点
                    not = i;
                    break;
                }
            }
            if (not == -1)
                break;// 找不到,结束
            for (int i = 1; i <= n; i++) {
                /*
                 *  遍历所有点, 每个点都和现有最外侧的点比较,得到新的最外侧的点
                 *  第二个条件是找到极点，不包括共线点
                 */
                if ((cross(point[in], point[i], point[not]) > 0)
                        || (cross(point[in], point[i], point[not]) == 0)
                        && (distance(point[in], point[i]) > distance(
                                point[in], point[not])))
                    not = i;
            }
            if (vis[not])
                break;// 找不到最外侧的点了
            queue.offer(not);// 最外侧的点进凸包
            vis[not] = true;// 标记这点已放进凸包了
            in = not;//in始终表示一个必定在凸包里的点
        }
        double ans = 0;
        in = 1;
        /*
         最后将point[1]的下标放进凸包
         不会重复放入，因为最开始只是把标记下标1在凸包
         */
        queue.offer(1);
        /*
         * 这里有个问题需要弄明白
         * 算凸多边形周长，需要连续的两个点，下面的是连续的不？
         * 是的。
         * 编号1插入到队尾，temp先取出的是队头，即是最后一个进入凸多边形的点，显然和编号1是连接的
         * 那会不会重复呢？
         * 当然不会，因为while循环最后一次是编号1和最先插入的点的距离，此时编号1已经没了，队列空了
         */
        while (!queue.isEmpty())
        {
            int temp = queue.poll();//获取并移除队列的头
            ans += Math.hypot((point[in].x - point[temp].x), (point[in].y - point[temp].y));
            in = temp;
        }
        System.out.println(ans);
    }
 
    public static void main(String args[]) {
        GiftWrap m = new GiftWrap();
        m.go();
    }
}

遗留问题：做完POJ1113时，想起了怎么求所得凸多边形的外接圆，也就是最小覆盖圆问题，那么又怎么求内切圆呢？