java 二叉搜索树

java二叉查找树实现：

二叉查找树，上图：比根节点小者在其左边，比根节点大者在其右边。

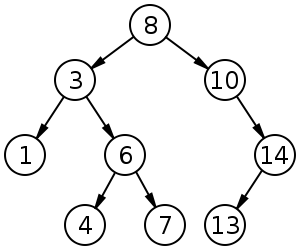
抽象数据结构，上代码：

/**
 * 二叉查找树数据结构(非线程安全)：
 * 范型类型须实现Comparable接口，用于比较操作
 */
public class BinarySearchTree<T extends Comparable<T>> {
    private Node<T> root; // tree root
    private int count;    // tree element counts

    /**
     * 内部节点类
     */
    private static class Node<E>{
        E value; //元素对象
        Node<E> parent; //父节点
        Node<E> left; //左孩子节点
        Node<E> right; //右孩子节点
        public Node(E value, Node<E> parent, Node<E> left, Node<E> right) {
            this.value = value;
            this.parent = parent;
            this.left = left;
            this.right = right;
        }
    }
}

一些基本操作实现：

• 插入(insert): 依次比较根元素，小者放左边，大者放右边：

/**
 * 插入元素
 * @param t 待插入元素
 * @return 插入成功返回true, 反之返回false
 */
public boolean insert(T t){
    if (root == null){ //若为空树
        root = new Node<T>(t, null, null, null);
        return true;
    }
    Node<T> newNode = new Node<T>(t, null, null, null);
    Node<T> pointer = root;
    while(true){
    if (newNode.value.compareTo(pointer.value) > 0){
        if (pointer.right == null){ //插入右边
        newNode.parent = pointer;
        pointer.right = newNode;
        count++;
        return true;
        } else{
        pointer = pointer.right;
        }
    } else if (newNode.value.compareTo(pointer.value) < 0){
        if (pointer.left == null){ //插入左边
        newNode.parent = pointer;
        pointer.left = newNode;
        count++;
        return true;
        } else{
        pointer = pointer.left;
        }
    } else { //相等了
        return false;
    }
    }
}

• 查找(get):

/**
 * 查找元素
 * @param t 待查找元素
 * @return 对应元素或null
 */
public T get(T t) {
    Node<T> n = getN(t);
    return n == null? null : n.value;
}

/**
 * 查找节点
 * @param t 待查找元素
 * @return 元素对应节点或null
 */
private Node<T> getN(T t) {
    Node<T> cur = root;
    while (cur != null){
        if (cur.value.compareTo(t) < 0){ //右边子树找
            cur = cur.right;
        } else if(cur.value.compareTo(t) > 0){ //左边子树找
            cur = cur.left;
        } else{ //找到该节点
            break;
        }
    }
    return cur;
}

• 查找最大，最小元素：

/**
 * 获取某节点为根的树的最小元素
 */
public T min(Node<T> n){
    Node<T> min = minN(n);
    return min == null ? null : min.value;
}

/**
 * 获取某节点为根的树的最小节点
 * @param n 树根节点
 * @return 该子树最小节点
 */
private Node<T> minN(Node<T> n){
    Node<T> min = n;
    while (min != null && min.left != null){
        min = min.left;
    }
    return min;
}
/**
 * 获取某节点为根的树的最大元素
 * @return 最大元素, 没有返回null
 */
public T max(Node<T> n){
    Node<T> max = maxN(n);
    return max == null ? null : max.value;
}

/**
 * 获取某节点为根的树的最大节点
 */
private Node<T> maxN(Node<T> n){
    Node<T> max = n;
    while (max != null && max.right != null){
        max = max.right;
    }
    return max;
}

• 遍历树(中序遍历):

/**
 * 中序遍历
 */
public void leftRootRight(){
    printLRR(root);
}

/**
 * 中序遍历打印元素
 */
private void printLRR(Node<T> node) {
    if (node != null){
        printLRR(node.left);
        System.out.println(node.value);
        printLRR(node.right);
    }
}

• 获取前驱(prev)元素：

主要有两种情况：

1.该节点左子树不为空：其前驱节点为其左子树的最大元素:

2.该节点左子树为空: 其前驱节点为其祖先节点(递归)，且该祖先节点的右孩子也为其祖先节点(就是一直往其parent找，出现左拐后的那个祖先节点)：

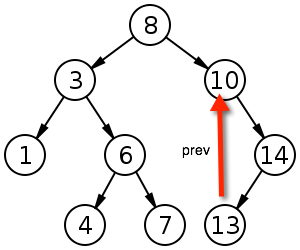
代码实现：

/**
 * 获取元素前驱(中序遍历)
 * @param t 指定元素
 * @return 元素前驱，没有返回null
 */
public T prev(T t){
    //先找到该元素
    Node<T> cur = getN(t);
    if (cur != null){
        return locatePrev(cur);
    }
    return null;
}

/**
 * 定位到前驱节点
 * @param cur 当前节点
 * @return 前驱节点，没有返回null
 */
private T locatePrev(Node<T> cur) {
    Node<T> prev = locatePrevN(cur);
    return prev == null ? null : prev.value;
}

/**
 * 定位到前驱节点
 * @param cur 当前节点
 * @return 当前节点的前驱节点
 */
private Node<T> locatePrevN(Node<T> cur){
    if (cur != null){
        //1.如果该节点左子树不会空，则其前驱为其左子树的最大元素
        if (cur.left != null) return maxN(cur.left);
        //2.该节点左子树为空, 则其前驱为：其祖先节点(递归), 且该祖先节点的右孩子也是其祖先节点
        //  通俗的说，一直忘上找找到左拐后那个节点;
        Node<T> p = cur.parent;
        while(p != null && cur == p.left){
            cur = p;
            p = p.parent;
        }
        return p == null ? null: p;
    }
    return null;
}

• 获取后继节点，也分两种情况：

1.该节点右子树不为空，其后继节点为其右子树的最小元素：

2.该节点右子树为空，其后继节点为其祖先节点(递归)，且此祖先节点的左孩子也是该节点的祖先节点，就是说一直往上找其祖先节点，直到出现右拐后的那个祖先节点：

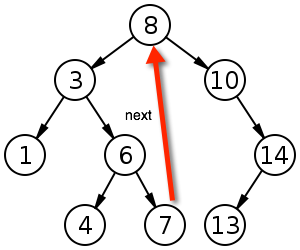
实现代码：

/**
 * 获取元素后继元素(中序遍历)
 * @param t 指定元素
 * @return 后继元素，没有返回null
 */
public T next(T t){
    //先找到该元素
    Node<T> cur = getN(t);
    if (cur != null){
        return locateNext(cur);
    }
    return null;
}

/**
 * 定位当前节点的后继元素
 * @param cur 当前节点
 * @return 其后继元素
 */
private T locateNext(Node<T> cur) {
    Node<T> next = locateNextN(cur);
    return next == null ? null : next.value;
}

/**
 * 定位到当前节点的后继节点
 * @param cur 当前节点
 * @return 当前节点的后继节点
 */
private Node<T> locateNextN(Node<T> cur) {
    if (cur == null) return null;
    //1.若其右子树不为空，那么其后继节点就是其右子树的最小元素
    if (cur.right != null) return minN(cur.right);
    //2.若为空，应该为其祖先节点(递归)，且该祖先节点的左孩子也是其祖先节点
    //  通俗的说，一直忘上找，找到右拐后那个节点;
    Node<T> p = cur.parent;
    while (p != null && cur == p.right){
        cur = p;
        p = p.parent;
    }
    return p;
}

• 删除(remove), 可分为三种情况：

1.该节点为叶子节点，直接删除：

2.该节点有一个孩子，将其孩子接上其父节点：

3.该节点有2个孩子，先删除其右子树的最小元素(该元素最多只会有一个孩子)，将这个最小元素去替换要删除的节点：

实现代码：

/**
 * 移除某元素
 * @param t 待删除元素
 * @return 删除成功返回true, 反之false
 */
public boolean remove(T t){
    //找到该节点
    Node<T> cur = getN(t);
    if (cur != null){
        if (doRemove(cur)){
            cur=null; count--;
            return true;
        }
    }
    return false;
}

/**
 * 执行删除操作
 */
private boolean doRemove(Node<T> cur) {
    //该节点是否为根
    boolean isRoot = cur == root;
    //1.该节点为叶子节点, 直接将其父节点对应(左或右)孩子置空
    if (cur.left == null && cur.right == null){
        if (isRoot) return true; //若树只有一个根节点
        if (cur == cur.parent.right) //该节点为父节点的右孩子
            cur.parent.right = null;
        else                    //该节点为父节点的左孩子
            cur.parent.left = null;
        return true;
    } else if(cur.left != null && cur.right != null){
        //2.该节点有2个孩子, 我们先找出一个替换节点(该节点的后继节点，后继节点没有则前驱节点)
        //找到其后继节点
        Node<T> replaceNode = locateNextN(cur);
        if (replaceNode == null) //若没有后继节点则用前驱节点
            replaceNode = locatePrevN(cur);
        doRemove(replaceNode);
        cur.value = replaceNode.value;
        return true;
    } else{ //3.该节点有1个孩子, 直接将其父节点对应(左或右)孩子接到其非空孩子
        Node<T> needLinkedNode = null;
        if (cur.left == null && cur.right != null){ //该节点有右孩子
            needLinkedNode = cur.right;
        } else if(cur.left != null && cur.right == null){ //该节点有左孩子
            needLinkedNode = cur.left;
        }
        if(isRoot){ //若该节点为根
            root = needLinkedNode;
            return true;
        }
        if (cur == cur.parent.right)  //该节点为父节点右孩子
            cur.parent.right = needLinkedNode;
        else
            cur.parent.left = needLinkedNode;
        return true;
    }
}