字符串匹配算法-BM

在用于查找子字符串的算法中，BM(Boyer-Moore)算法是当前有效且应用比较广泛的一种算法，各种文本编辑器的“查找”功能（Ctrl+F），大多采用Boyer-Moore算法。比我们学习的KMP算法快3~5倍。

在1977年，Boyer-Moore算法由德克萨斯大学的Robert S. Boyer教授和J Strother Moore教授发明

下面通过Java实现BM算法：

package com.buaa;

import java.util.Random;

/**
* @ProjectName StringPatternMatchAlgorithm
* @PackageName com.buaa
* @ClassName BM
* @Description TODO
* @Author 刘吉超
* @Date 2016-05-26 22:26:08
*/
public class BM {
    /**
     * 利用坏字符规则计算移动位数
     */
    public static int badCharacter(String moduleString, char badChar,int badCharSuffix){
        return badCharSuffix - moduleString.lastIndexOf(badChar, badCharSuffix);
    }

    /**
     * 利用好后缀规则计算移动位数
     */
    public static int goodCharacter(String moduleString,int goodCharSuffix){
        int result = -1;
        // 模式串长度
        int moduleLength = moduleString.length();
        // 好字符数
        int goodCharNum = moduleLength -1 - goodCharSuffix;

        for(;goodCharNum > 0; goodCharNum--){
            String endSection = moduleString.substring(moduleLength - goodCharNum, moduleLength);
            String startSection = moduleString.substring(0, goodCharNum);
            if(startSection.equals(endSection)){
                result = moduleLength - goodCharNum;
            }
        }

        return result;
    }

    /**
     * BM匹配字符串
     *
     * @param originString 主串
     * @param moduleString 模式串
     * @return 若匹配成功，返回下标，否则返回-1
     */
    public static int match(String originString, String moduleString){
        // 主串
        if (originString == null || originString.length() <= 0) {
            return -1;
        }
        // 模式串
        if (moduleString == null || moduleString.length() <= 0) {
            return -1;
        }
        // 如果模式串的长度大于主串的长度，那么一定不匹配
        if (originString.length() < moduleString.length()) {
            return -1;
        }

        int moduleSuffix = moduleString.length() -1;
        int module_index = moduleSuffix;
        int origin_index = moduleSuffix;

        for(int ot = origin_index; origin_index < originString.length() && module_index >= 0;){
            char oc = originString.charAt(origin_index);
            char mc = moduleString.charAt(module_index);
            if(oc  == mc){
                origin_index--;
                module_index--;
            }else{
                // 坏字符规则
                int badMove = badCharacter(moduleString,oc,module_index);
                // 好字符规则
                int goodMove = goodCharacter(moduleString,module_index);
                 // 下面两句代码可以这样理解，主串位置不动，模式串向右移动
                origin_index = ot + Math.max(badMove, goodMove);
                 module_index = moduleSuffix;
                 // ot就是中间变量
                 ot = origin_index;
            }
        }

        if(module_index < 0){
            // 多减了一次
            return origin_index + 1;
        }

        return -1;
    }

    /**
     * 随机生成字符串
     *
     * @param length 表示生成字符串的长度
     * @return String
     */
    public static String generateString(int length) {
        String baseString = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789";     

        StringBuilder result = new StringBuilder();

        Random random = new Random();
        for (int i = 0; i < length; i++) {
            result.append(baseString.charAt(random.nextInt(baseString.length())));
        }

        return result.toString();
     }

    public static void main(String[] args) {
        // 主串
//        String originString = generateString(10);
        String originString = "HERE IS A SIMPLE EXAMPLE";
        // 模式串
//        String moduleString = generateString(4);
        String moduleString = "EXAMPLE";
        // 坏字符规则表
//        int[] badCharacterArray = badCharacter(originString,moduleString);

        System.out.println("主串：" + originString);
        System.out.println("模式串：" + moduleString);

        int index = match(originString, moduleString);
        System.out.println("匹配的下标：" + index);
    }
}

下面，我来解释上面代码

首先先明确两个规则：坏字符规则、好后缀规则

1、坏字符规则

后移位数 = 坏字符的位置 - 模式串中的坏字符上一次出现位置

如果"坏字符"不包含在模式串之中，则上一次出现位置为 -1。以下面这两个字符串为例

因为"P"与"E"不匹配，所以"P"被称为"坏字符"，它出现在模式串（模式串就是EXAMPLE）的第6位（从0开始编号），在模式串中的上一次出现位置为4，所以后移 6 - 4 = 2位

2、好后缀规则

后移位数 = 好后缀的位置 - 模式串中的上一次出现位置

举例来说，如果模式串"ABCDAB"的后一个"AB"是"好后缀"。那么它的位置是5（从0开始计算，取最后的"B"的值），在模式串中的上一次出现位置是1（第一个"B"的位置），所以后移 5 - 1 = 4位，前一个"AB"移到后一个"AB"的位置。

再举一个例子，如果模式串"ABCDEF"的"EF"是好后缀，则"EF"的位置是5 ，上一次出现的位置是 -1（即未出现），所以后移 5 - (-1) = 6位，即整个字符串移到"F"的后一位。

这个规则有三个注意点：

（1）"好后缀"的位置以最后一个字符为准。假定"ABCDEF"的"EF"是好后缀，则它的位置以"F"为准，即5（从0开始计算）。

　     （2）如果"好后缀"在模式串中只出现一次，则它的上一次出现位置为 -1。比如，"EF"在"ABCDEF"之中只出现一次，则它的上一次出现位置为-1（即未出现）。

（3）如果"好后缀"有多个，这时应该选择最长的那个"好后缀"且它的上一次出现位置必须在头部。比如，假定"BABCDAB"的"好后缀"是"DAB"、"AB"、"B"，这时"好后缀"的上一次出现位置是什么？回答是，此时采用的好后缀是"B"，它的上一次出现位置是头部，即第0位，其他好后缀上一次出现的位置都不在头部

规则讲完啦，接下说一下上面代码

1、假定主串为"HERE IS A SIMPLE EXAMPLE"，模式串为"EXAMPLE"，模式串也就是搜索词

主串	HERE IS A SIMPLE EXAMPLE
模式串	EXAMPLE

2、首先，主串与模式串头部对齐，从尾部开始比较。这是一个很聪明的想法，因为如果尾部字符不匹配，那么只要一次比较，就可以知道前7个字符（整体上）肯定不是要找的结果。我们看到，"S"与"E"不匹配。这时，"S"就被称为"坏字符"（bad character），这时用坏字符规则得到的是7，用好后缀规则得到的是-1，选择大的作为后移位数，这里选择7

3、依然从尾部开始比较，发现"P"与"E"不匹配，所以"P"是"坏字符"。

4、这时用坏字符规则得到的是2，用好后缀规则得到的是-1，选择大的作为后移位数，这里选择2

5、依然从尾部开始比较，"E"与"E"匹配。

6、比较前面一位，"LE"与"LE"匹配。

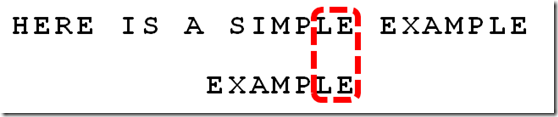
7、比较前面一位，"PLE"与"PLE"匹配

8、比较前面一位，"MPLE"与"MPLE"匹配。我们把这种情况称为"好后缀"（good suffix），即所有尾部匹配的字符串。注意，"MPLE"、"PLE"、"LE"、"E"都是好后缀

9、比较前一位，发现"I"与"A"不匹配。所以，"I"是"坏字符"，这时用坏字符规则得到的是3，用好后缀规则得到的是6，选择大的作为后移位数，这里选择6

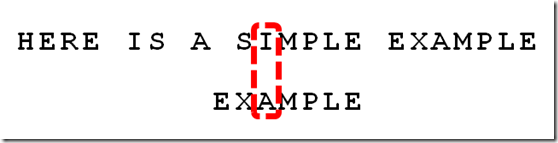
10、继续从尾部开始比较，"P"与"E"不匹配，因此"P"是"坏字符"。这时用坏字符规则得到的是2，用好后缀规则得到的是-1，选择大的作为后移位数，这里选择2

11. 从尾部开始逐位比较，发现全部匹配，于是搜索结束

如果，您认为阅读这篇博客让您有些收获，不妨点击一下右下角的【推荐】。
如果，您希望更容易地发现我的新博客，不妨点击一下左下角的【关注我】。
如果，您对我的博客所讲述的内容有兴趣，请继续关注我的后续博客，我是【刘超★ljc】。

本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。