Breadth-first search 算法（Swift版）

在讲解Breadth-first search 算法之前，我们先简单介绍两种数据类型Graph和Queue。

Graph

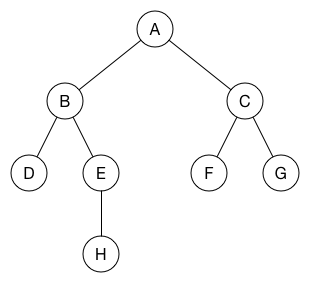
这就是一个图，它由两部分组成：

• 节点， 使用圆圈表示的部分
• 边， 使用线表示的地方，通常都是有方向的线

这种数据结构可以形象的表示一个网络,而在实际解决问题的时候，我们除了找到类似网络的模拟外，还需要考虑下边两点：

• 需要找到某条路径
• 需要找到到达某个节点的最短路径

而如何实现这个查找的过程就用到了算法。

在项目管理专业的工程方法中，存在一个有向连接图方法，根据这个图我们就可以划出邻接矩阵，然后再求出可达矩阵，缩减矩阵等等，说这些内容，是想表达在用代码模拟图的时候，可以使用矩阵的方式来描述，但本篇中采用的是另一种方式，我们使用数组保存某个节点的neighbor节点。

上边一段话会在下边的代码中进行展示：

Graph.swift
// MARK: - Edge
public class Edge: Equatable {
  public var neighbor: Node
  public init(neighbor: Node) {
    self.neighbor = neighbor
  }
}
public func == (lhs: Edge, rhs: Edge) -> Bool {
  return lhs.neighbor == rhs.neighbor
}
// MARK: - Node
public class Node: CustomStringConvertible, Equatable {
  public var neighbors: [Edge]
  public private(set) var label: String
  public var distance: Int?
  public var visited: Bool
  public init(label: String) {
    self.label = label
    neighbors = []
    visited = false
  }
  public var description: String {
    if let distance = distance {
      return "Node(label: \(label), distance: \(distance))"
    }
    return "Node(label: \(label), distance: infinity)"
  }
  public var hasDistance: Bool {
    return distance != nil
  }
  public func remove(edge: Edge) {
    neighbors.remove(at: neighbors.index { $0 === edge }!)
  }
}
public func == (lhs: Node, rhs: Node) -> Bool {
  return lhs.label == rhs.label && lhs.neighbors == rhs.neighbors
}
// MARK: - Graph
public class Graph: CustomStringConvertible, Equatable {
  public private(set) var nodes: [Node]
  public init() {
    self.nodes = []
  }
  public func addNode(_ label: String) -> Node {
    let node = Node(label: label)
    nodes.append(node)
    return node
  }
  public func addEdge(_ source: Node, neighbor: Node) {
    let edge = Edge(neighbor: neighbor)
    source.neighbors.append(edge)
  }
  public var description: String {
    var description = ""
    for node in nodes {
      if !node.neighbors.isEmpty {
        description += "[node: \(node.label) edges: \(node.neighbors.map { $0.neighbor.label})]"
      }
    }
    return description
  }
  public func findNodeWithLabel(_ label: String) -> Node {
    return nodes.filter { $0.label == label }.first!
  }
  public func duplicate() -> Graph {
    let duplicated = Graph()
    for node in nodes {
      _ = duplicated.addNode(node.label)
    }
    for node in nodes {
      for edge in node.neighbors {
        let source = duplicated.findNodeWithLabel(node.label)
        let neighbour = duplicated.findNodeWithLabel(edge.neighbor.label)
        duplicated.addEdge(source, neighbor: neighbour)
      }
    }
    return duplicated
  }
}
public func == (lhs: Graph, rhs: Graph) -> Bool {
  return lhs.nodes == rhs.nodes
}

Queue

队列同样是一种数据结构，它遵循FIFO的原则，因为Swift没有现成的这个数据结构，因此我们手动实现一个。

值得指出的是，为了提高性能，我们针对在数组中读取数据做了优化。比如，当在数组中取出第一个值时，如果不做优化，那么这一步的消耗为O(n),我们采取的解决方法就是把该位置先置为nil，然后设置一个阈值，当达到阈值时，在对数组做进不去的处理。

这一部分的代码相当简单

Queue.swift
public struct Queue<T> {
    fileprivate var array = [T?]()
    fileprivate var head = 0
    public init() {
    }
    public var isEmpty: Bool {
        return count == 0
    }
    public var count: Int {
        return array.count - head
    }
    public mutating func enqueue(_ element: T) {
        array.append(element)
    }
    public mutating func dequeue() -> T? {
        guard head < array.count, let element = array[head] else { return nil }
        array[head] = nil
        head += 1
        let percentage = Double(head) / Double(array.count)
        if array.count > 50 && percentage > 0.25 {
            array.removeFirst(head)
            head = 0
        }
        return element
    }
    public var front: T? {
        if isEmpty {
            return nil
        } else {
            return array[head]
        }
    }
}

Breadth-first search

其实这个算法的思想也很简单，我们已源点为中心，一层一层的往外查找，在遍历到某一层的某个节点时，如果该节点是我们要找的数据，那么就退出循环，如果没找到，那么就把该节点的neighbor节点加入到队列中，这就是该算法的核心原理。

打破循环的条件需要根据实际情况来设定。

//: Playground - noun: a place where people can play
import UIKit
import Foundation
var str = "Hello, playground"
func breadthFirstSearch(_ graph: Graph, source: Node) -> [String] {
    /// 创建一个队列并把源Node放入这个队列中
    var queue = Queue<Node>()
    queue.enqueue(source)
    /// 创建一个数组用于存放结果
    var nodesResult = [source.label]
    /// 设置Node的visited为true，因为我们会把这个当做一个开关
    source.visited = true
    /// 开始遍历
    while let node = queue.dequeue() {
        for edge in node.neighbors {
            let neighborNode = edge.neighbor
            if !neighborNode.visited {
                queue.enqueue(neighborNode)
                neighborNode.visited = true
                nodesResult.append(neighborNode.label)
            }
        }
    }
    return nodesResult
}
let graph = Graph()
let nodeA = graph.addNode("a")
let nodeB = graph.addNode("b")
let nodeC = graph.addNode("c")
let nodeD = graph.addNode("d")
let nodeE = graph.addNode("e")
let nodeF = graph.addNode("f")
let nodeG = graph.addNode("g")
let nodeH = graph.addNode("h")
graph.addEdge(nodeA, neighbor: nodeB)
graph.addEdge(nodeA, neighbor: nodeC)
graph.addEdge(nodeB, neighbor: nodeD)
graph.addEdge(nodeB, neighbor: nodeE)
graph.addEdge(nodeC, neighbor: nodeF)
graph.addEdge(nodeC, neighbor: nodeG)
graph.addEdge(nodeE, neighbor: nodeH)
graph.addEdge(nodeE, neighbor: nodeF)
graph.addEdge(nodeF, neighbor: nodeG)
let nodesExplored = breadthFirstSearch(graph, source: nodeA)
print(nodesExplored)

总结

实现的代码不是重点，重要的是理解这些思想，在实际情况中能够得出解决的方法。当然跟实现的语言也没有关系。

使用playground时，command + 1可以看到Source文件夹，把单独的类放进去就可以加载进来了。上边的内容来自这个网站swift-algorithm-club