图的BFS

目录：

　　一、算法的基本思路

　　二、算法过程

　　三、题目：785判断是否为二分图

https://blog.csdn.net/weixin_40953222/article/details/80544928

一、算法的基本思路

广度优先搜索类似于树的层次遍历过程。

它需要借助一个队列来实现。如图2-1-1所示，要想遍历从v0到v6的每一个顶点，我们可以设v0为第一层，v1、v2、v3为第二层，v4、v5为第三层，v6为第四层，再逐个遍历每一层的每个顶点。

具体过程如下：

1.准备工作：

　　创建一个visited数组，用来记录已被访问过的顶点；

　　创建一个队列，用来存放每一层的顶点；

　　初始化图G。

2.从图中的v0开始访问，将的visited[v0]数组的值设置为true，同时将v0入队。

3.只要队列不空，则重复如下操作：

　　(1)队头顶点u出队。

　　(2)依次检查u的所有邻接顶点w，若visited[w]的值为false，则访问w，并将visited[w]置为true，同时将w入队。

二、过程：

白色表示未被访问，灰色表示即将访问，黑色表示已访问。

visited数组：0表示未访问，1表示以访问。

队列：队头出元素，队尾进元素。

1.初始时全部顶点均未被访问，visited数组初始化为0，队列中没有元素。

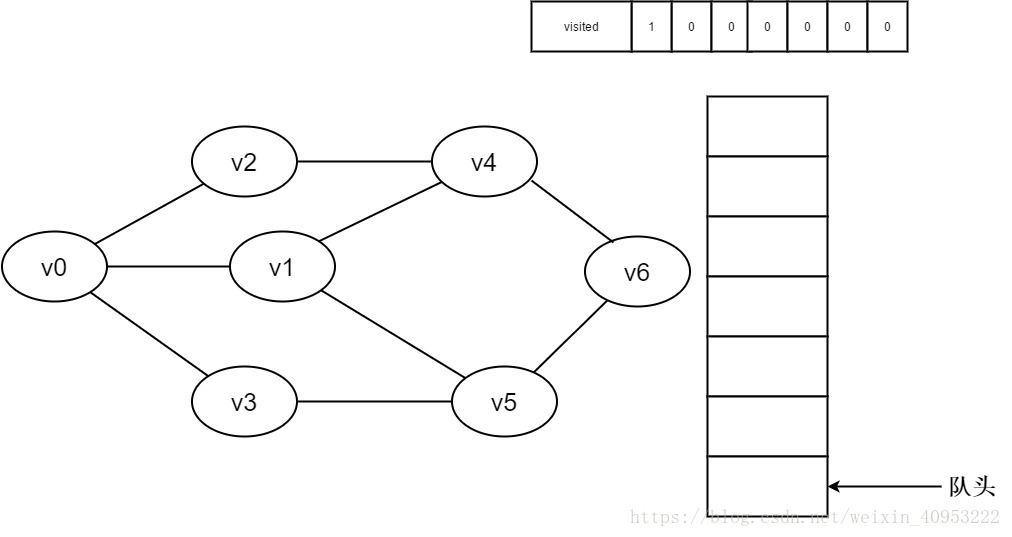
2.即将访问顶点v0。

　

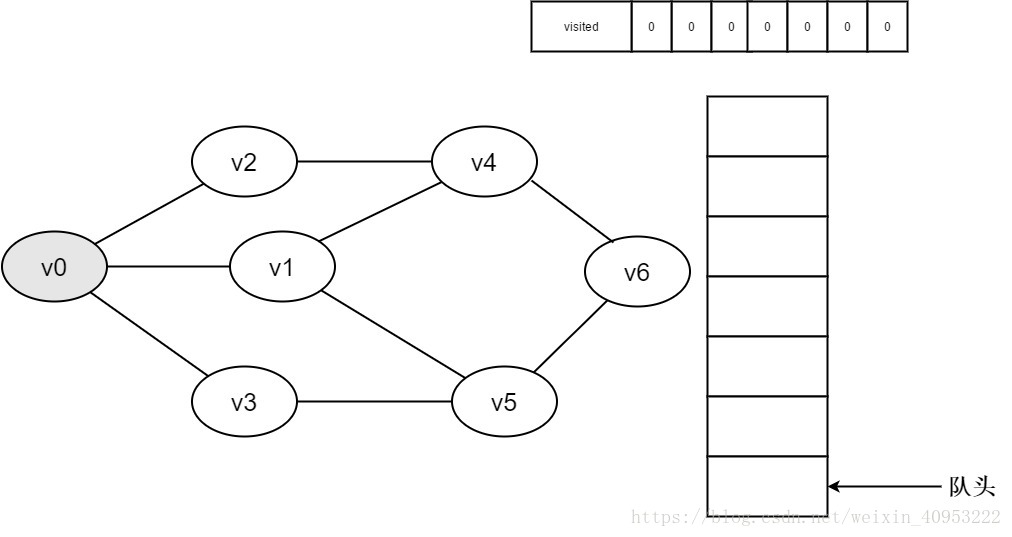
3.访问顶点v0，并置visited[0]的值为1，同时将v0入队。

4.将v0出队，访问v0的邻接点v2。判断visited[2]，因为visited[2]的值为0，访问v2。

5.将visited[2]置为1，并将v2入队。

6.访问v0邻接点v1。判断visited[1],因为visited[1]的值为0，访问v1。

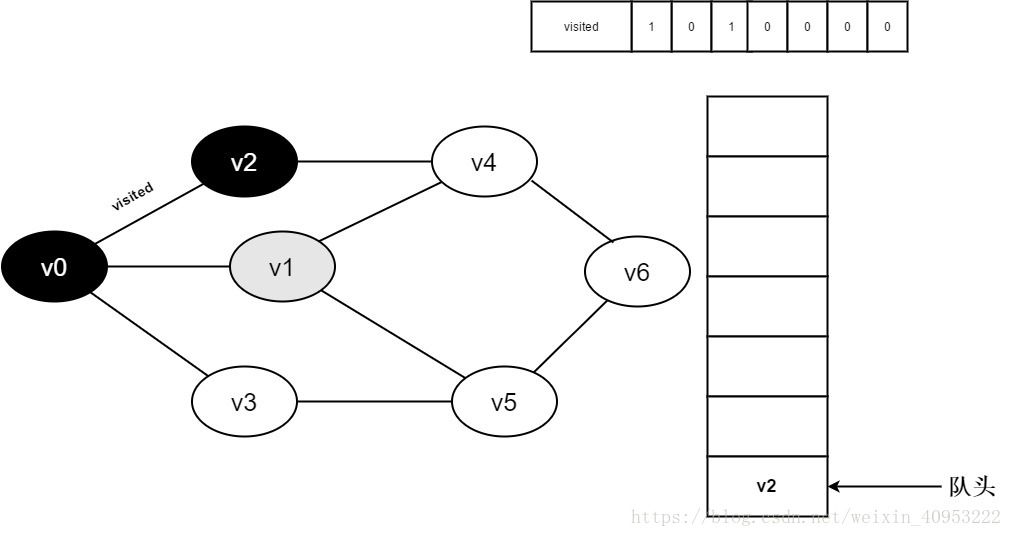
7.将visited[1]置为0，并将v1入队。

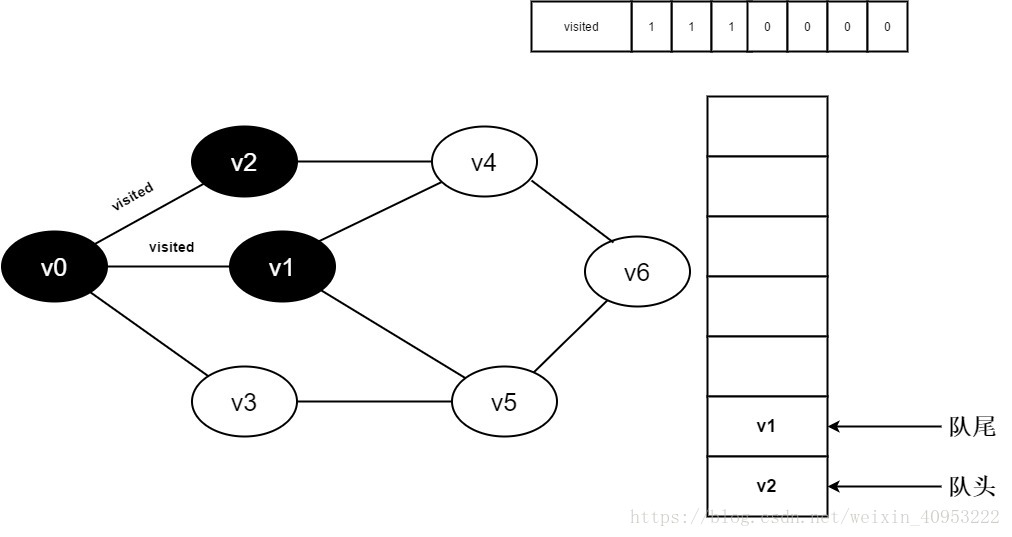
8.判断visited[3],因为它的值为0，访问v3。将visited[3]置为0，并将v3入队。

9.v0的全部邻接点均已被访问完毕。将队头元素v2出队，开始访问v2的所有邻接点。

开始访问v2邻接点v0，判断visited[0]，因为其值为1，不进行访问。

继续访问v2邻接点v4，判断visited[4]，因为其值为0，访问v4，如下图：

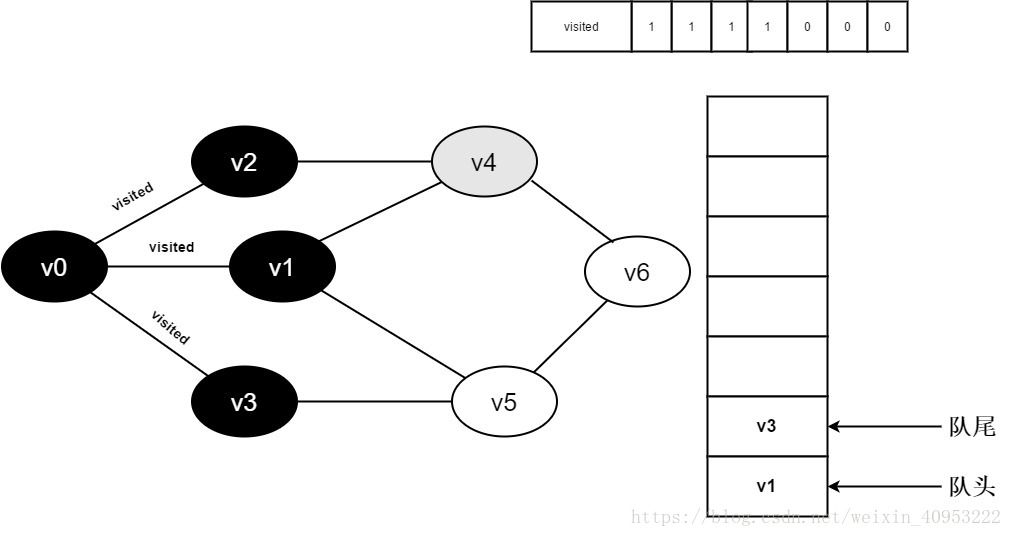
10.将visited[4]置为1，并将v4入队。

11.v2的全部邻接点均已被访问完毕。

将队头元素v1出队，开始访问v1的所有邻接点。开始访问v1邻接点v0，因为visited[0]值为1，不进行访问。

继续访问v1邻接点v4，因为visited[4]的值为1，不进行访问。

继续访问v1邻接点v5，因为visited[5]值为0，访问v5，如下图：

12.将visited[5]置为1，并将v5入队。

　　

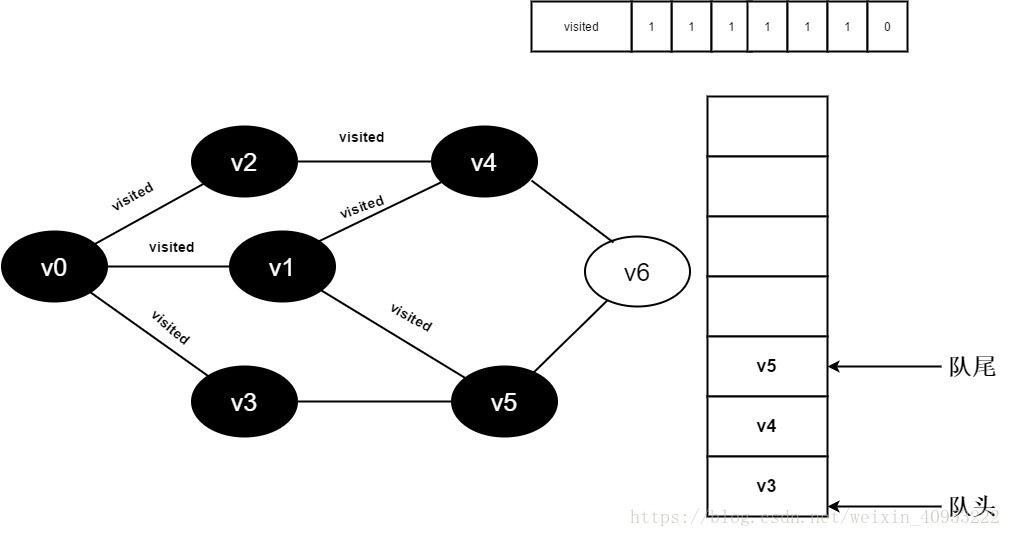
13.v1的全部邻接点均已被访问完毕，将队头元素v3出队，开始访问v3的所有邻接点。

开始访问v3邻接点v0，因为visited[0]值为1，不进行访问。

继续访问v3邻接点v5，因为visited[5]值为1，不进行访问。

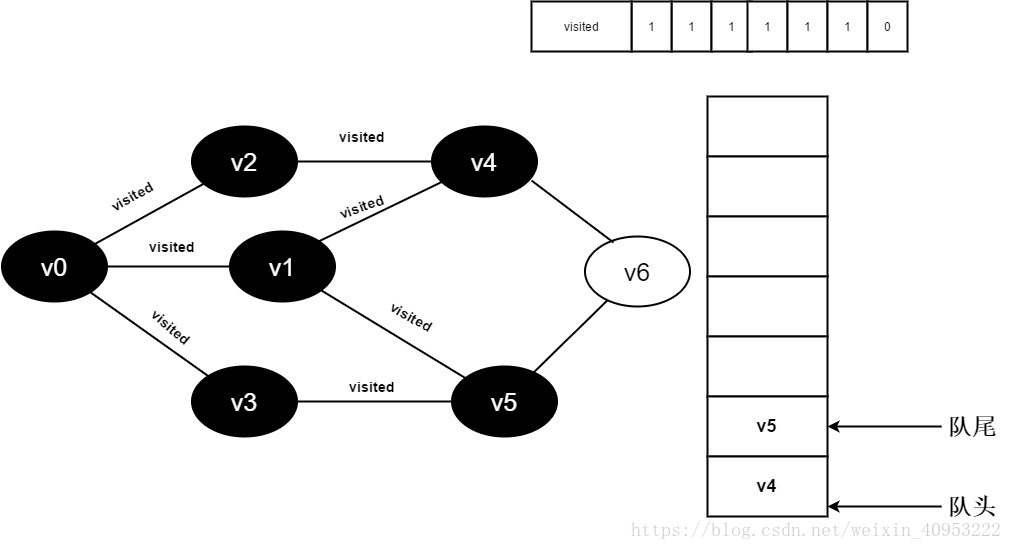
14.v3的全部邻接点均已被访问完毕，将队头元素v4出队，开始访问v4的所有邻接点。

开始访问v4的邻接点v2，因为visited[2]的值为1，不进行访问。

继续访问v4的邻接点v6，因为visited[6]的值为0，访问v6，如下图：

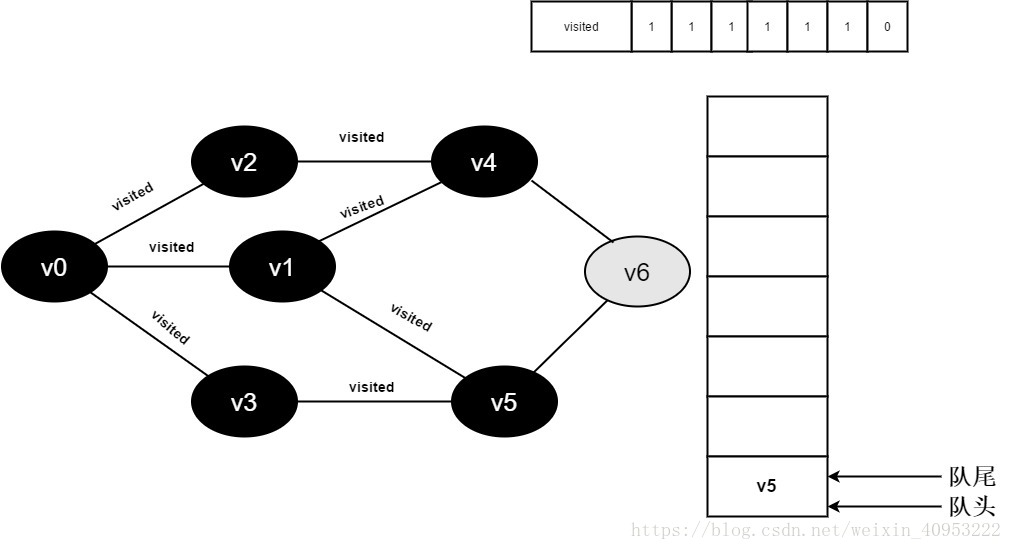
15.将visited[6]值为1，并将v6入队。

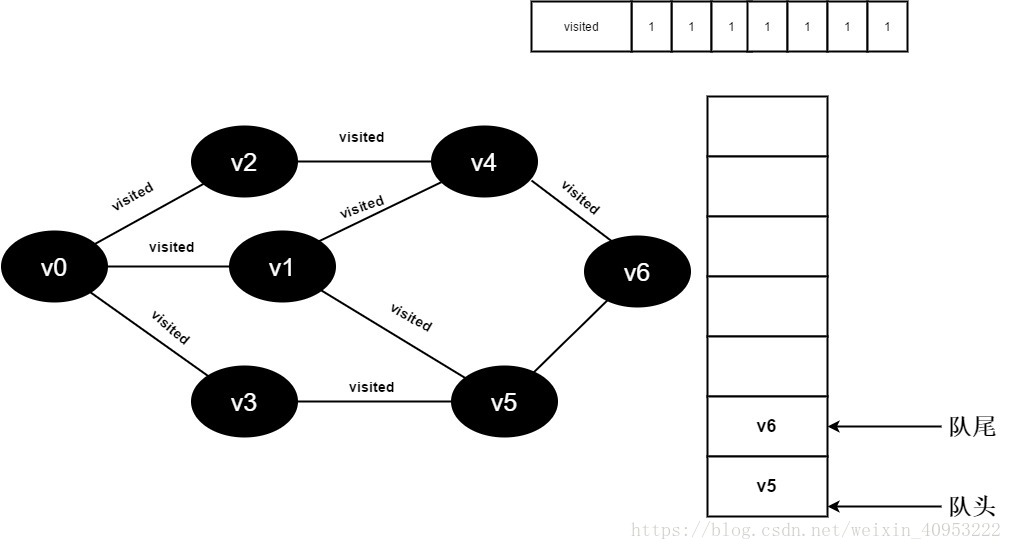
16.v4的全部邻接点均已被访问完毕，将队头元素v5出队，开始访问v5的所有邻接点。

开始访问v5邻接点v3，因为visited[3]的值为1，不进行访问。

继续访问v5邻接点v6，因为visited[6]的值为1，不进行访问。

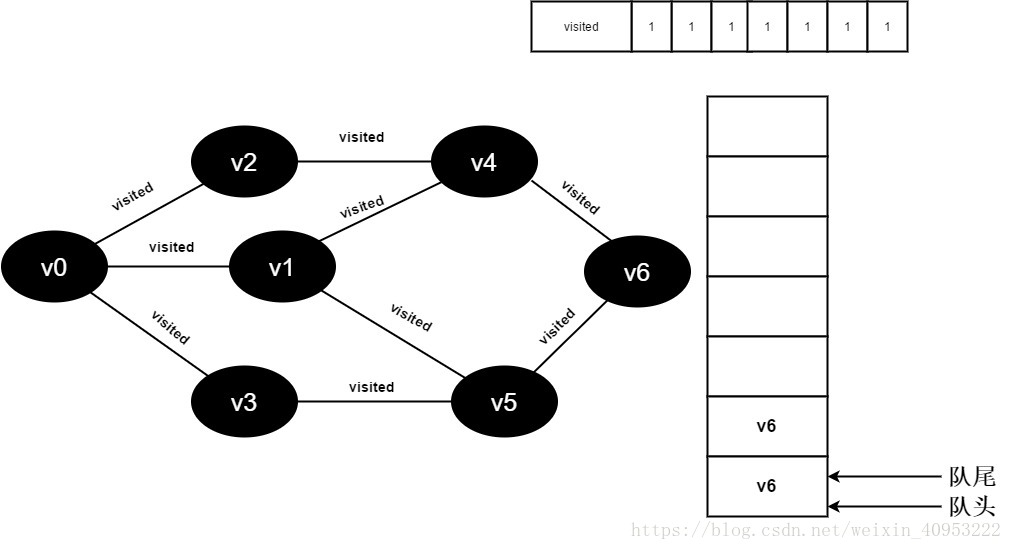
17.v5的全部邻接点均已被访问完毕，将队头元素v6出队，开始访问v6的所有邻接点。

开始访问v6邻接点v4，因为visited[4]的值为1，不进行访问。

继续访问v6邻接点v5，因为visited[5]的值文1，不进行访问。

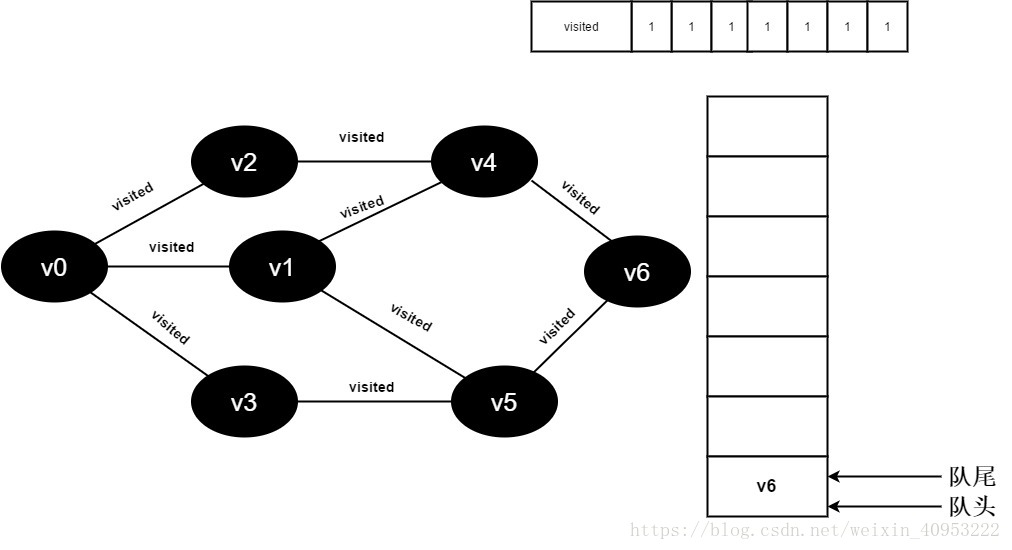
18.队列为空，退出循环，全部顶点均访问完毕。

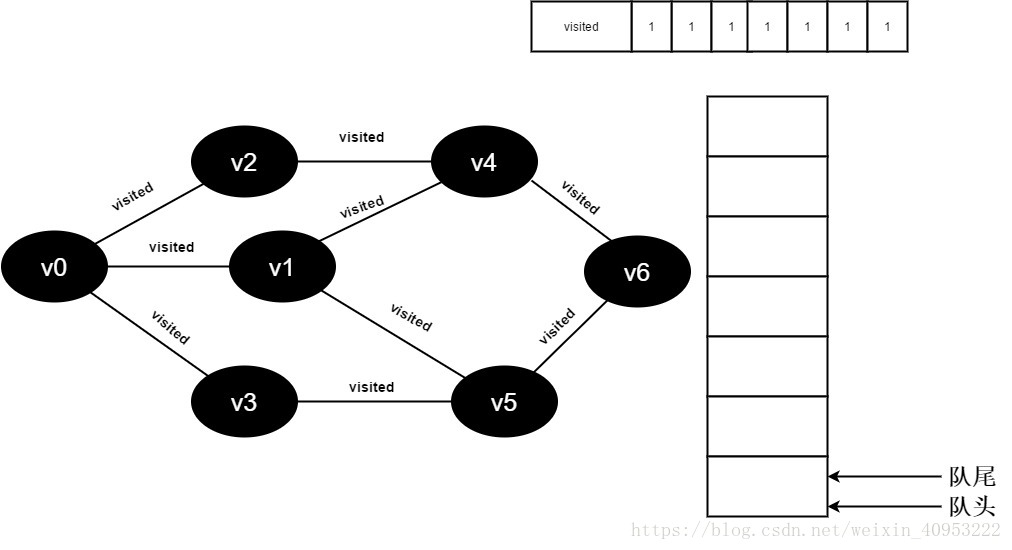
题目：785判断二分图

给定一个无向图graph，当这个图为二分图时返回true。

如果我们能将一个图的节点集合分割成两个独立的子集A和B，并使图中的每一条边的两个节点一个来自A集合，一个来自B集合，我们就将这个图称为二分图。

graph将会以邻接表方式给出，graph[i]表示图中与节点i相连的所有节点。每个节点都是一个在0到graph.length-1之间的整数。这图中没有自环和平行边： graph[i] 中不存在i，并且graph[i]中没有重复的值。

示例 1:
输入: [[1,3], [0,2], [1,3], [0,2]]
输出: true
解释:
无向图如下:
0----1
|    |
|    |
3----2
我们可以将节点分成两组: {0, 2} 和 {1, 3}。

示例 2:
输入: [[1,2,3], [0,2], [0,1,3], [0,2]]
输出: false
解释:
无向图如下:
0----1
| \  |
|  \ |
3----2
我们不能将节点分割成两个独立的子集。

注意:

• graph 的长度范围为 [1, 100]。
• graph[i] 中的元素的范围为 [0, graph.length - 1]。
• graph[i] 不会包含 i 或者有重复的值。
• 图是无向的: 如果j 在 graph[i]里边, 那么 i 也会在 graph[j]里边。

思路：

分析: 用染色法，即从其中一个顶点开始，将跟它邻接的点染成与其不同的颜色，如果邻接的点有相同颜色的，则说明不是二分图

代码：

def bfs(s,graph,color,queue):
    color[s] = 1
    queue.append(s)
    while queue:
        u = queue.pop()
        print(u)
        for v in graph[u]:
            if color[v] == 0:
                queue.append(v)
                color[v] = 0 - color[u]
            else:
                if color[v] == color[u]:
                    return False
    return True

def isBipartite(graph):
    if not graph:
        return False
    n = len(graph)
    color = [0] * n
    queue = []
    for i in range(n):
        if color[i] == 0 and not bfs(i,graph,color,queue):
            return False
    return True
graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
isBipartite(graph)