Matlab随笔之插值与拟合（上）

原文:Matlab随笔之插值与拟合（上）

1、拉格朗日插值

新建如下函数：

function y=lagrange(x0,y0,x)
%拉格朗日插值函数
%n 个节点数据以数组 x0, y0 输入(注意 Matlat 的数组下标从1开始),
%m 个插值点以数组 x 输入,输出数组 y 为 m 个插值
n=length(x0);m=length(x);
for i=:m
z=x(i);
s=0.0;
for k=:n
      p=1.0;
      for j=:n
           if j~=k
              p=p*(z-x0(j))/(x0(k)-x0(j));
           end
      end
      s=p*y0(k)+s;
end
y(i)=s;
end

应用实例：

x0=1:1:20;
y0=x0.^2-20*x0-5;
x=1:0.1:20;
z=lagrange(x0,y0,x);
plot(x,z,':',x0,y0,'ko');

运行结果：

2、分段线性插值

MATLAB现成的插值函数为interp1，其调用格式为：  yi= interp1(x,y,xi,'method')

其中x，y为插值点，yi为在被插值点xi处的插值结果；x,y为向量， 'method'表示采用的插值方法，包括：
'method'：是最近项插值;                                                              'linear'：线性插值;（默认）

'spline'：逐段3次样条插值; (下面的三次样条插值会用到)             'cubic'：保凹凸性3次插值

'pchip'：分段三次Hermite 插值。

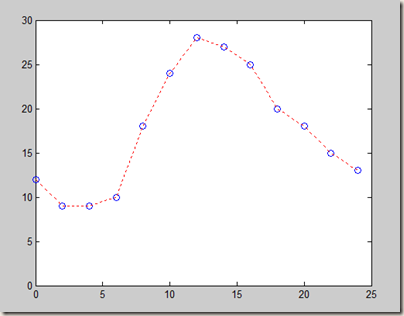
例如：在一天24小时内，从零点开始每间隔2小时测得的环境温度数据分别为
            12，9，9，1，0，18 ，24，28，27，25，20，18，15，13，
推测中午12点（即13点）时的温度．

x=::;
y=[,,,,,,,,,,,,];
x1=:0.5:;
y1=interp1(x,y,x1,'linear');
plot(x,y,'bo',x1,y1,'r:');

运行结果：

3、埃尔米特插值

如果要求插值函数不仅在节点处与函数同值，而且要求它与函数有相同的一阶、二阶甚至高阶导数值，这就是埃尔米特插值问题。

已知f（x）的n+1个节点的函数值f（xi）以及导数值f`（xi），可得一个至多n+1次的多项式H（x），即hermite插值多项式。

新建以下这个函数：

function y = hermite( x0,y0,y1,x )
%埃尔米特插值多项式
%x0为点横坐标
%y0为函数值
%y1为导数值
%m个插值点用数组x输入
n=length(x0);m=length(x);
for k=:m
    yy=0.0;
    for i=:n
     h=1.0;
     a=0.0;
      for j=:n
         if j~=i
           h=h*((x(k)-x0(j))/(x0(i)-x0(j)))^;
           a=/(x0(i)-x0(j))+a;
         end
      end
      yy=yy+h*((x0(i)-x(k))*(*a*y0(i)-y1(i))+y0(i));
end
y(k)=yy;
end

4、样条插值

所谓样条（ Spline）本来是工程设计中使用的一种绘图工具，它是富有弹性的细木条或细金属条。绘图员利用它把一些已知点连接成一条光滑曲线（称为样条曲线），并使连接点处有连续的曲率。

数学上将具有一定光滑性的分段多项式称为样条函数。

在实际中最常用的是二次样条函数和三次样条函数：

二次样条函数插值

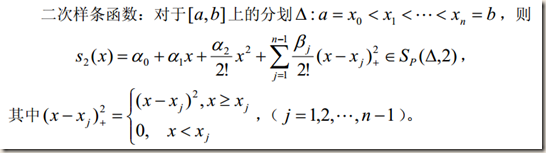
首先，我们注意到s2 (x)中含有 n + 2 个特定常数，故应需要 n + 2 个插值条件，因此，二次样条插值问题可分为两类：

（1）已知插值节点xi 和相应的函数值 yi (i = 0,1,…,n) 以及端点 x0 （或 xn ）处的导数值y'0（或y'n）

（2）已知插值节点xi 和相应的导数值 y'i (i = 0,1,…,n) 以及端点 x0 （或 xn ）处的函数值y0 （或yn ）

三次样条函数插值

由于 s3 (x)中含有n + 3 个待定系数，故应需要 n + 3 个插值条件，已知插值节点xi 和相应的函数值 f(xi ) = yi (i = 0,1,…,n) ，这里提供了 n + 1 个条件，还需要 2 个边界条件。因此，三次样条插值问题可分为三类：

（1）s'3 (a) = y'0 ,s'3 (b) = y'n 。由这种边界条件建立的样条插值函数称为 f(x) 的完备三次样条插值函数。
特别地,y0' = yn`= 0时，样条曲线在端点处呈水平状态。
如果 f' (x) 不知道，我们可以要求 s'3 (x) 与 f' (x) 在端点处近似相等。这时以x0 , x1 , x2 , x3 为节点作一个三次 Newton 插值多项式 Na (x) ，以 xn, xn−1, xn−2, xn−3 作一个三次 Newton 插值多项式 Nb (x) ，要求s' (a) = N'a (a), s' (b) = N'b (b)
由这种边界条件建立的三次样条称为 f(x) 的 Lagrange 三次样条插值函数。

（2）s"3 (a) = y"0 ,s"3 (b) = y"3 。特别地 y"n = y"n = 0 时，称为自然边界条件。

（3）s'3 ( a + 0) = s'3 ( b − 0), s"3 (a + 0) = s"3 (b − 0) ， (这里要求 s3 (a + 0) =s3 (b − 0) )此条件称为周期条件。

Matlab实现（三次样条插值）

Matlab中的函数：

1、y=interp1(x0,y0,x,`spline`);%(spline改成linear，则变成线性插值)

2、y=spline(x0,y0,xi);%这个是根据己知的x，y数据，用样条函数插值出xi处的值。即由x,y的值计算出xi对应的函数值。

3、pp=spline(x0,y0);%是由根据己知的x，y数据，求出它的样条函数表达式，不过该表达式不是用矩阵直接表示，要求点x`的值，要用函数y`=ppval(pp,x`);

4、pp=csape(x,y,'变界类型','边界值conds');生成各种边界条件的三次样条插值. 其中,(x,y)为数据向量,边界类型可为:

'complete'：给定边界一阶导数,即默认的边界条件,Lagrange边界条件
             'not-a-knot'：非扭结条件,不用给边界值.
             'periodic'：周期性边界条件,不用给边界值.
             'second'：给定边界二阶导数. 
             'variational'：自然样条(边界二阶导数为[0,0]

边界值conds可用1x2矩阵表示,矩阵元素取值为1,2,此时，使用命令
pp=csape(x0,y0_ext,conds)
其中 y0_ext=[left, y0, right]，这里 left 表示左边界的取值， right 表示右边界的取值。
conds(i)=j 的含义是给定端点 i 的 j 阶导数， 即 conds 的第一个元素表示左边界的条
件，第二个元素表示右边界的条件， conds=[2,1]表示左边界是二阶导数，右边界是一阶
导数，对应的值由 left 和 right 给出。

例子：

表 1
x  0  3      5   7     9  11  12  13  14  15
y  0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6
要求用 Lagrange、分段线性和三次样条三种插值方法计算。

编程实现：

clear,clc
x0=[,,,,,,,,,];
y0=[,1.2,1.7,2.0,2.1,2.0,1.8,1.2,1.0,1.6];
t=:0.05:;
%拉格朗日插值函数
y1=lagrange(x0,y0,t);%调用编写的lagrange函数
dy1=(lagrange(x0,y0,0.0001)-lagrange(x0,y0,))/0.0001%x=0处斜率
min1=min(lagrange(x0,y0,:0.001:))%13到15最小值
subplot(,,);
plot(x0,y0,'ro',t,y1);%画出曲线
title('拉格朗日插值函数');
%分段线性插值
y2=interp1(x0,y0,t,'spline');%注意区分spline与linear
Y2=interp1(x0,y0,t);%默认linear
dy2=(interp1(x0,y0,0.0001,'spline')-interp1(x0,y0,,'spline'))/0.0001%x=0处斜率
min2=min(interp1(x0,y0,:0.001:,'spline'))%13到15最小值
subplot(,,);
plot(t,y2,'b',t,Y2,'r',x0,y0,'ro');%画出曲线
title('分段线性插值');
legend('边条','线性');%显示图形图例
%三次线条插值A
y3=spline(x0,y0,t);
dy3=(spline(x0,y0,0.0001)-spline(x0,y0,))/0.0001%x=0处斜率
min3=min(spline(x0,y0,:0.001:))%13到15最小值
subplot(,,);
plot(x0,y0,'ro',t,y3);%画出曲线
title('三次线条插值A');
%三次线条插值B
pp1=csape(x0,y0);%默认的边界条件,即给定边界一阶导数
pp2=csape(x0,y0,'second');%给定边界二阶导数
y4=ppval(pp1,t);
Y4=ppval(pp2,t);
dy4=(ppval(pp1,0.0001)-ppval(pp1,))/0.0001%x=0处斜率
min4=min(ppval(pp1,:0.001:))%13到15最小值
subplot(,,);
plot(t,y4,'b',t,Y4,'r',x0,y0,'ro');%画出曲线
title('三次线条插值B');
legend('一阶','二阶');

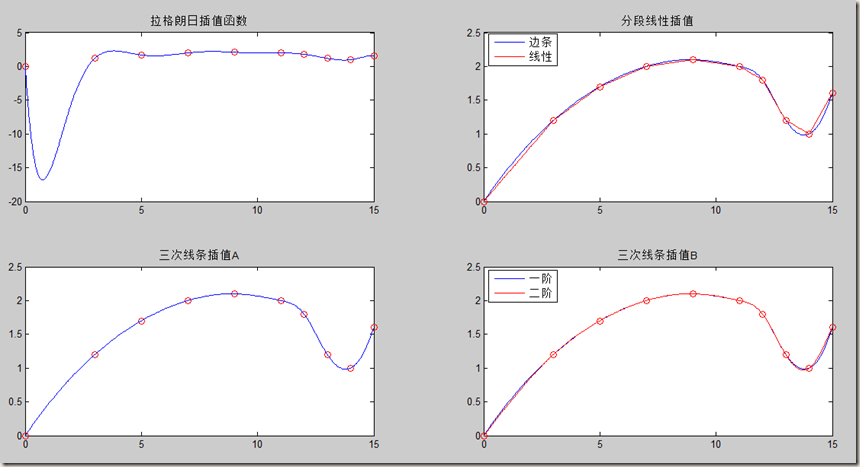
运行结果：

dy1 =
 
  -55.2855
 
min1 =
 
    0.9391
 
dy2 =
 
    0.5023
 
min2 =
 
    0.9828
 
dy3 =
 
    0.5023
 
min3 =
 
    0.9828
 
dy4 =
 
    0.5007
 
min4 =
 
    0.9851

综上，可以看出，拉格朗日插值函数根本不能应用，分段线性函数的光滑性较差，推荐三次样条插值。

同时，可以看出，interp1(x0,y0,’spline’)等价于spline(x0,y0)。

最后，将上述所有情况封装起来，变成下列函数：

function y = showAllInterp( x0,y0,s,t)
%显示x0,y0之间所有不同类型的插值情况
%字符串s选择要输出的插值类型：
%all：全部类型           lagrange：拉格朗日插值函数
%linear：分段线性插值    spline：三次线条插值A
%csape：三次线条插值B
if(nargin<)
    t=linspace(x0(),x0(length(x0)),);%默认
end
switch s
    case 'lagrange' %拉格朗日插值函数
        y1=lagrange(x0,y0,t);%调用编写的lagrange函数
        plot(x0,y0,'ro',t,y1);%画出曲线
        title('拉格朗日插值函数');
        if(nargout==)
            y=y1;
        end
    case 'linear' %分段线性插值
        y2=interp1(x0,y0,t);%默认linear
        plot(x0,y0,'ro',t,y2,'b');%画出曲线
        title('分段线性插值');
        if(nargout==)
            y=y2;
        end
    case 'spline' %三次线条插值A
        y3=spline(x0,y0,t); %等价于interp1(x0,y0,t,'spline');
        plot(x0,y0,'ro',t,y3);%画出曲线
        title('三次线条插值A');
        if(nargout==)
            y=y3;
        end
    case 'csape' %三次线条插值B
        pp1=csape(x0,y0);%默认的边界条件,即给定边界一阶导数
        pp2=csape(x0,y0,'second');%给定边界二阶导数
        y4=ppval(pp1,t);
        Y4=ppval(pp2,t);
        plot(t,y4,'b',t,Y4,'r',x0,y0,'ro');%画出曲线
        title('三次线条插值B');
        legend('一阶','二阶');
        if(nargout==)
            y=y4;
        end
    case 'all' %显示全部
        y1=lagrange(x0,y0,t);%调用编写的lagrange函数
        subplot(,,);
        plot(x0,y0,'ro',t,y1);%画出曲线
        title('拉格朗日插值函数');
 
        y2=interp1(x0,y0,t);%默认linear
        subplot(,,);
        plot(x0,y0,'ro',t,y2);%画出曲线
        title('分段线性插值');
 
        y3=spline(x0,y0,t); %等价于interp1(x0,y0,t,'spline');
        subplot(,,);
        plot(x0,y0,'ro',t,y3);%画出曲线
        title('三次线条插值A');
 
        pp1=csape(x0,y0);%默认的边界条件,即给定边界一阶导数
        pp2=csape(x0,y0,'second');%给定边界二阶导数
        y4=ppval(pp1,t);
        Y4=ppval(pp2,t);
        subplot(,,);
        plot(t,y4,'b',t,Y4,'r',x0,y0,'ro');%画出曲线
        title('三次线条插值B');
        legend('一阶','二阶');
end