[ACM] HDU 1400 Mondriaan's Dream （状态压缩,长2宽1长方形铺满）

Mondriaan's Dream

Time Limit: 20000/10000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 783    Accepted Submission(s): 506

Problem Description

Squares and rectangles fascinated the famous Dutch painter Piet Mondriaan. One night, after producing the drawings in his 'toilet series' (where he had to use his toilet paper to draw on, for all of his paper was filled with
squares and rectangles), he dreamt of filling a large rectangle with small rectangles of width 2 and height 1 in varying ways. 








Expert as he was in this material, he saw at a glance that he'll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won't turn into a nightmare! 

 

Input

The input file contains several test cases. Each test case is made up of two integer numbers: the height h and the width w of the large rectangle. Input is terminated by h=w=0. Otherwise, 1<=h,w<=11. 

 

Output

For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical tilings multiple times.

 

Sample Input

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

 

Sample Output

1
0
1
2
3
5
144
51205

 

Source

University of Ulm Local Contest
2000

解题思路：

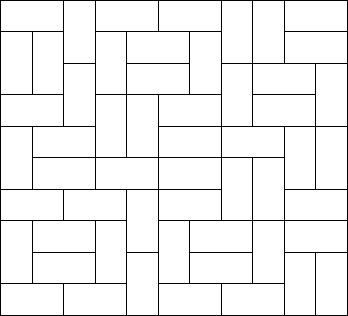
如图：问铺满大举行一共同拥有多少种方法。

由于长宽最大11，能够状态压缩.

从第一行開始铺砖。

dp[ i ]  [ j ] 定义为 第i行的状态为 j 一共同拥有多少种方法 .

把小矩形用01状态表示，小矩形由两个正方形组成。 对于横着放的小矩形，左右两个正方形用11表示，对于竖着的小矩形，上下两个正方形用分别01表示。

第i行的状态s2与第i-1行的状态s1有关。

s1和s2满足两个条件：

1.   s1  |  s2  得到的数二进制每一位都是1 ，由于对于竖着放的 ，0|1肯定是1，横着放的都是11，相或也是11.

2.   s1  & s2  得到的数连续的1是偶数个，注意0也是偶数。这个看图观察就能够了。

本题犯的错误：

1.

获取一个数x二进制的第i位是0或者1。用 if( x&(1<<i) ==1) 是不正确的， 这句话的意思是，把x的二进制数除了第i位都设为0，第i位通过 &1,来推断是0或者1，可是得到的数不一定是1，是2的倍数，比方 0010  或者 0100.

2.

推断一个数x二进制的每一位是否等于1 ，如果有m位 ， 直接用 if( x==1<<m)-1),不用每一位的推断。前者效率更高。

代码：

#include <iostream>
#include <stdlib.h>
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <string.h>
using namespace std;
#define ll long long
ll dp[12][1<<12];//dp[i][j]表示第i行状态为j有多少种方法
int n,m;

bool ok(int s1,int s2)
{
    int temp=s1|s2;//两个状态或运算每一位都必须是1
    if(temp!=(1<<m)-1)
        return false;
    int cnt=0;
    temp=s1&s2;//两个状态且运算，必须连续的1都是偶数个
    for(int i=0;i<m;i++)
    {
        if((temp&(1<<i)))//第i位是1
            cnt++;
        else
        {
            if(cnt&1)
                return false;
        }
    }
    if(cnt&1)
        return false;
    return true;
}

void solve()
{
    memset(dp,0,sizeof(dp));
    int maxd=1<<m;
    for(int i=0;i<maxd;i++)//铺第一行
        if(ok(maxd-1,i))
            dp[1][i]++;
    for(int i=2;i<=n;i++)//铺第i行
    {
        for(int j=0;j<maxd;j++)
        {
            for(int k=0;k<maxd;k++)
                if(ok(j,k))
                    dp[i][j]+=dp[i-1][k];
        }
    }
    ll ans=0;
    ans+=dp[n][maxd-1];//最后一行肯定都是1
    printf("%I64d\n",ans);
}

int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        if(!n||!m)
            break;
        if(n*m&1)//小方块的个数为奇数个，肯定不能铺满
        {
            printf("0\n");
            continue;
        }
        if(n<m)
            n=n^m,m=n^m,n=n^m;
        solve();
    }
    return 0;
}