算法导论————KMP

【例题传送门：caioj1177】

---

KMP模版：子串是否出现

【题意】
有两个字符串SA和SB，SA是母串，SB是子串，问子串SB是否在母串SA中出现过。
如果出现过输出第一次出现的起始位置和结束位置，否则输出"NO"
【输入文件】
第一行SA（1<= 长度<=1000000）
第二行SB（1<= 长度<=1000）
【输出文件】
如果SB在SA中出现过输出第一次出现的起始位置和结束位置，否则输出"NO"
【样例1输入】
aaaaabaa
aab
【样例1输出】
4 6
【样例2输入】
aaaaabaa
aax
【样例2输出】
NO

---

算法分析：

　　KMP其实就是一种偷懒的方式，通过访问前面已经遍历过的位置来首先给定一个可继承的值，然后暴力（汗......）

　　首先定义一个p数组，p[i]=j时，代表SA字符串[1...j]与SA字符串[i-j+1...i]所形成的子串完全相同

　　那么我们怎么得出这个p数组呢？

　　就是暴力+偷懒！！！（其实前面已经讲了，尴尬）

　　当我们访问到i这个点时，我们先访问一下i-1，因为我们访问到i的时候已经把1~i-1的p数组求出来了，那么请看下面的图：

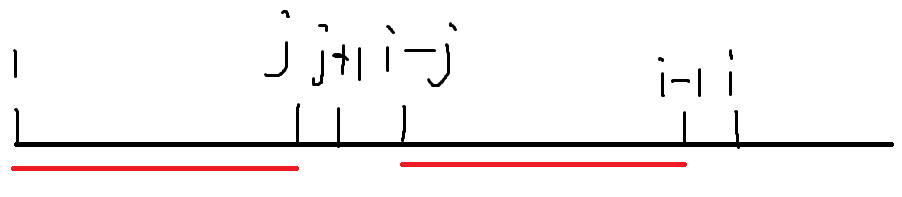
　　我们设j=p[i-1]，i-1-j+1=i-j，那么我们可以知道SA[1...j]=SA[i-j...i-1]，也就是上图的红色区间，那假如SA[j+1]=SA[i]的话，我们就可以直接p[i]=j+1对吧

　　但是现实是残酷的（AC没有那么容易~），那么当SA[j+1]!=SA[i]的时候怎么办呢？那么我们就找p[j]！！！如图：

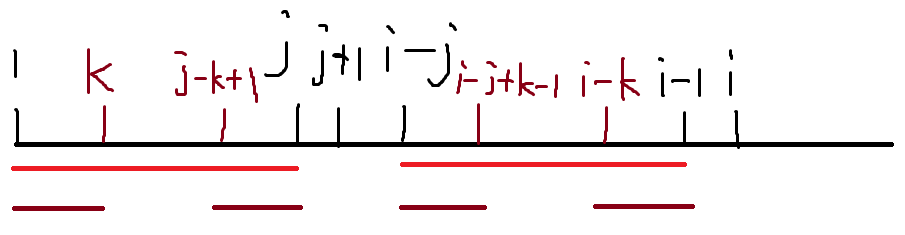
　　我们再设一个变量k=p[j]，因为p[j]的定义，所以我们可以得到SA[1...k]=SA[j-k+1...j]，也就是前两个棕色区间，这时因为两个红色区间相同，所以我们可以得到SA[1...k]=SA[i-j...i-j+k-1]，也就是第一个和第三个棕色区间相等，接着又可以得到SA[j-k+1...j]=SA[i-k(i-1-k+1)...i-1]，也就是第二个和第四个的棕色区间相等，然后！！！我们得到四个棕色区间相等！！！我们就可以判断SA[k+1]和SA[i]是否相等来求p[i]，如果相等，p[i]=k+1，否则继续找p[k]。一直找啊找，直到找到没得找也就是当前的p[p[p[p[p[p[.......的值为0时，那么我们就判断SA[1]和SA[i]是否相同，相同p[i]=1，否则p[i]=0

　　其实也不算暴力，而是利用p数组的定义来寻找前面可以用来继承的点！！

　　但是到了这里，还没有完成KMP的学习

　　我们的p数组只对SA字符串，也就是题目中的子串进行了处理

　　那么p数组对于我们求答案有什么帮助呢？

　　

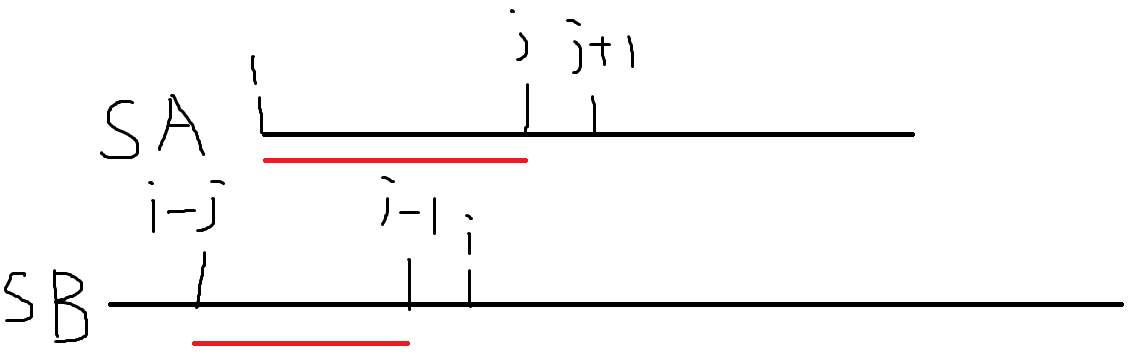
　　我们设j为SB字符串中的i-1位置开始所组成的后缀，与SA字符串中的1位置开始的前缀的最长公共长度，也就是SA[1...j]=SB[i-j(i-1-j+1)...j-1]，那么我们可以判断SA[j+1]和SB[i]是否相等，相等就记录j的值，不相等就找p[j]！！！是不是似曾相识的步骤，没错！就是把SB中的i转移到SA中进行求解，这样就是KMP的全部了！

---

参考代码：

#include<cstdio>
#include<cstring>
using namespace std;
char sa[],sb[];//sa是母串，sb是子串
int p[];//p数组是为子串准备的，p的含义和母串一点关系都没有。
//p[i]表示sb中 以第i个字符为结尾，往前最多拉多少个字符（sb[i]结尾的后缀）可以完全匹配sb的前缀
//比如  sb="abcdabc"中 p[7]=3, 就这样，我当你理解p[i]的含义了
int main()
{
    int lena,lenb,i,j;
    scanf("%s",sa+);lena=strlen(sa+);
    scanf("%s",sb+);lenb=strlen(sb+);
    //制造P数组
    p[]=;
    for(i=;i<=lenb;i++)
    {
        j=p[i-];//先记录p[i-1]
        while(j>&&sb[i]!=sb[j+]) j=p[j];
        /*
        这里有两种情况
        如果j+1的位置的字符等于i位置的字符的话，那就直接把p[i]=j+1
        否则就找j的p值，因为1~sb[p[j]]一定是1~sb[j]的后缀
        */
        if(sb[i]==sb[j+]) p[i]=j+;else p[i]=;
    }
    int st,ed;
    j=;
    for(i=;i<=lena;i++)//紧接着用p数组来匹配母串
    {
        while(j>&&sa[i]!=sb[j+]) j=p[j];
        if(sa[i]==sb[j+]) j++;
        if(j==lenb){ed=i;st=i-lenb+;break;}//得到答案后就记录开头与结尾
    }
    if(j==lenb) printf("%d %d\n",st,ed);
    else printf("NO\n");
    return ;
}