LDA学习笔记

线性判别分析（Linear Discriminant Analysis，简称LDA）是一种经典的线性学习方法。其思想非常朴素，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近，异类的样例的投影点尽可能的远离，在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定样本的类别。

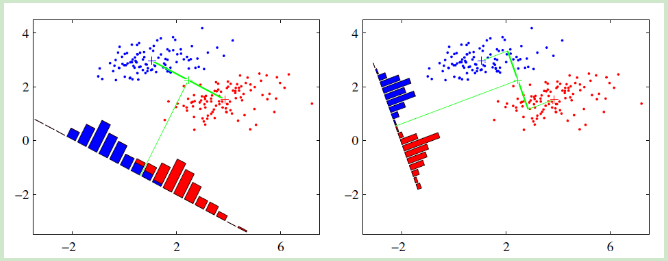
右图要比左图的投影效果好，因为右图的红色数据和蓝色数据各个较为集中，且类别之间的距离明显。左图则在边界处数据混杂。以上就是LDA的主要思想了，当然在实际应用中，我们的数据是多个类别的，我们的原始数据一般也是超过二维的，投影后的也一般不是直线，而是一个低维的超平面。

二类LDA原理

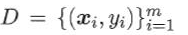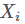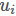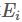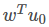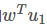给定数据集，​ 第i类示例的集合， 第i类示例的均值向量， 第i类示例的协方差矩阵， 两类样本的中心在直线上的投影：和，​ 两类样本的协方差：

，欲使同类样例的投影尽可能的接近，可以让同类样例投影点的协方差尽可能小，即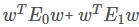 尽可能的小；而欲使异类样例的投影点尽可能远离，可以让类中心之间的距离尽可

能大，即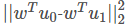  尽可能大，同时考虑二者，则可得到欲最大化的目标

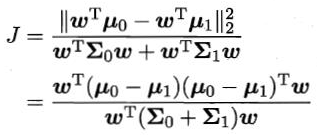
定义“类内散度矩阵”

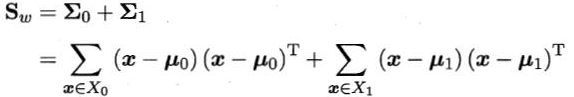
以及“类间散度矩阵”

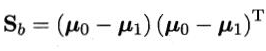
则J可重写为

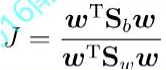
这就是LDA欲最大化的目标，即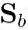与的“广义瑞丽商”

首先该式子分子和分母都是关于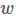的二次项，因此解与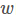的长度无关，只和方向有关。（如果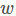是一个解，那么对于任意常数α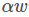，也是一个解。）。不失一般性，可令分母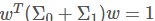那么原式等价于：

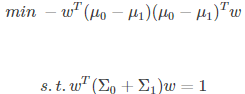
对于式子的求解，一般可用拉格朗日乘子法解决，同时LDA同样适用于多分类的问题。

补充：

• 从贝叶斯决策理论的角度可以证明LDA在两类数据同先验、满足高斯分布且协方差相等时，LDA可达到最优分类。
•  LDA核心是投影，这样往往实现了降维，因而LDA也常被视为一种经典的监督降维技术。