聚类算法（二）--BIRCH

BIRCH (balanced iterative reducing and clustering using hierarchies)（名字太长不用管了）

无监督，适合大样本的聚类方法。大多数情况只需扫描一次数据集。(文中有下划线的均表示向量）

一句话概括BIRCH，就是根据某种距离度量方法将数据簇已CF形式表现出来，又根据一定规则在CF树上排列（看不懂没关系）

下面我们展开说。

先讲CF

首先CF代表的是数据簇，哪怕是只有一个点，也看做簇

定义CF（N,LS,SS），N代表数据簇的样本点个数，LS表示数据点同一特征之和，SS表示所有样本点特征值平方值和。

举例说明。

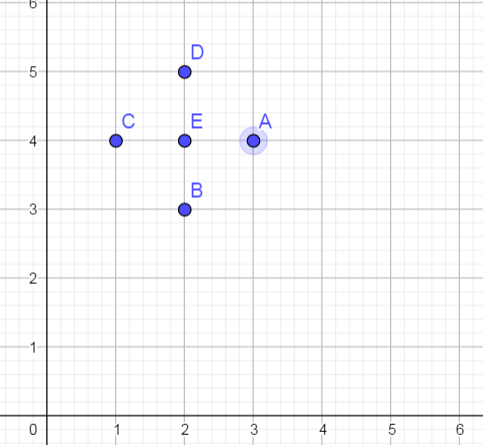
假设上述五点属于一个CF，A(3,4),B(2,3),C(1,4),D(2,5),E(2,4)

N=5,LS=(3+2+1+2+2,4+3+4+5+4)=(10,20),SS=9+16+4+9+1+16+4+25+4+16=104

所以CF=[5,(10,20),104]

那么，CF有个容易理解的性质--可加性，CF1=CF2+CF3=(N2+N3,LS2+LS3,SS2+SS3)

CF还有几个参数：

形心（Centroid）：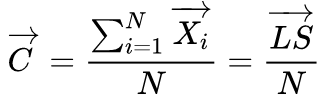

半径（radius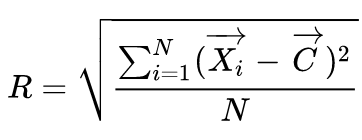）：（表示为簇内一点到形心的距离，类似于标准差，所以可以变换成标准差的计算，$\sqrt{\frac{NSS-LS^{2}}{N^{2}}}$）

（簇内所有点两两之间的平均距离）$\delta =\sqrt{\frac{\sum \sum \left (x_{i}-\overrightarrow{c}  \right )^{2}(x_{j}-\overrightarrow{c})^{2}}{N(N-1)}}$

R和δ都表示了簇的紧实度。

某种距离度量方法

即簇与簇之间的距离的度量D，比如

欧几里得距离$\sqrt{(\frac{\sum LS_{1}}{N_{1}}-\frac{\sum LS_{2}}{N_{2}})^{2}}$

曼哈顿距离$\left | \frac{\sum LS_{1}}{N_{1}}-\frac{\sum LS_{2}}{N_{2}} \right |$

一定规则在CF树上排列

一定规则指的是CF树的参数，枝平衡因子β（一个枝节点包含叶节点个数的上限），叶平衡因子λ（一个叶节点包含CF个数的上限），空间阈值τ（簇与簇距离的上限）

这里建造的CF树不保留数据原始信息，只有CF，所以起到压缩数据的作用

现在我们看看如何造树

一棵树一般有根节点（RN,root node），枝节点(BN,branch node)，叶节点(LN,leaf node)。

1,首先第一个数据进来，建造CF1，作为根节点。（无任何限制）

2,第二个数据进来，建造CF2，计算簇与簇之间的距离D，若D<τ，将这两点视为同一簇，更新CF1.若D>空间阈值τ，将CF1,CF2都作为枝节点；

3,上面两步只讲到了增加或者膨胀节点，如何分裂节点呢？

举例说明，

在红色情况下设定枝平衡因子β=3，叶平衡因子λ=3，

进来一个新样本点sc8，他与叶节点LN1,2,3中LN1的距离最近，所以应该归入LN1叶节点，

计算sc8与sc1,2,3的距离，均大于空间阈值τ，所以不能并入sc1,2,3，需要给他成为一个独立的簇，

但是由于叶平衡因子λ=3，即一个叶节点包含簇个数的上限为3，所以要将叶节点LN1分裂成两个LN1',LN1''。

但是此时相当于有四个叶节点LN1',LN1''，LN2,LN3，又枝平衡因子β=3，即一个枝节点包含叶节点个数的上限为3，

所以将根节点（本应该为枝节点，此例无枝节点）也一分为二，如下图

还有一个问题，刚才的四个簇sc8,1,2,3，如何分入叶节点LN1',LN1''

求这四个簇相距最远的最为LN1',LN1''的种子CF，将剩余的簇分别计算与种子CF的距离，距离近的归到一个叶节点

具体解释，假设sc8,1,2,3中，sc8和sc2最远，先将这两个簇放入不同的叶节点，然后分别计算sc1,sc3与sc8和sc2的距离，较近的归为种子CF所在的叶节点。

BIRCH适用于大样本，与Mini Batch K-Means类似，但是BIRCH适用于K较大的情况，Mini Batch K-Means适用K适中或较小

当维度较大时，Mini Batch K-Means比BIRCH表现的好。

参考：

https://www.cnblogs.com/pinard/p/6179132.html

https://www.cnblogs.com/tiaozistudy/p/6129425.html

https://en.wikipedia.org/wiki/BIRCH