剑指Offer面试题：33.二叉树的深度

一、题目一：二叉树的深度

1.1 题目说明

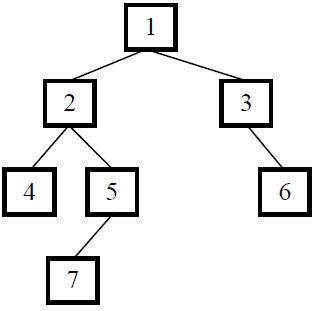
题目一：输入一棵二叉树的根结点，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度。例如下图中的二叉树的深度为4，因为它从根结点到叶结点最长的路径包含4个结点（从根结点1开始，经过结点2和结点5，最终到达叶结点7）。

　　二叉树的结点定义如下，这里使用C#语言描述：

    public class BinaryTreeNode
    {
        public int Data { get; set; }
        public BinaryTreeNode LeftChild { get; set; }
        public BinaryTreeNode RightChild { get; set; }
 
        public BinaryTreeNode(int data)
        {
            this.Data = data;
        }
 
        public BinaryTreeNode(int data, BinaryTreeNode left, BinaryTreeNode right)
        {
            this.Data = data;
            this.LeftChild = left;
            this.RightChild = right;
        }
    }

1.2 解题思路

　　①如果一棵树只有一个结点，它的深度为1。

　　②如果根结点只有左子树而没有右子树，那么树的深度应该是其左子树的深度加1；同样如果根结点只有右子树而没有左子树，那么树的深度应该是其右子树的深度加1。

　　③如果既有右子树又有左子树，那该树的深度就是其左、右子树深度的较大值再加1。

　　比如在上图的二叉树中，根结点为1的树有左右两个子树，其左右子树的根结点分别为结点2和3。根结点为2的左子树的深度为3，而根结点为3的右子树的深度为2，因此根结点为1的树的深度就是4。

    public static int GetTreeDepth(BinaryTreeNode root)
    {
        if (root == null)
        {
            return ;
        }
 
        int left = GetTreeDepth(root.LeftChild);
        int right = GetTreeDepth(root.RightChild);
 
        return left >= right ? left +  : right + ;
    }

1.3 单元测试

　　（1）测试用例

    [TestClass]
    public class TreeDepthTest
    {
        private void SetSubTreeNode(BinaryTreeNode root, BinaryTreeNode lChild, BinaryTreeNode rChild)
        {
            if (root == null)
            {
                return;
            }
 
            root.LeftChild = lChild;
            root.RightChild = rChild;
        }
 
        private void ClearUpTreeNode(BinaryTreeNode root)
        {
            if (root != null)
            {
                BinaryTreeNode left = root.LeftChild;
                BinaryTreeNode right = root.RightChild;
 
                root = null;
 
                ClearUpTreeNode(left);
                ClearUpTreeNode(right);
            }
        }
 
        //            1
        //         /      \
        //        2        3
        //       /\         \
        //      4  5         6
        //        /
        //
        [TestMethod]
        public void GetDepthTest1()
        {
            BinaryTreeNode node1 = new BinaryTreeNode();
            BinaryTreeNode node2 = new BinaryTreeNode();
            BinaryTreeNode node3 = new BinaryTreeNode();
            BinaryTreeNode node4 = new BinaryTreeNode();
            BinaryTreeNode node5 = new BinaryTreeNode();
            BinaryTreeNode node6 = new BinaryTreeNode();
            BinaryTreeNode node7 = new BinaryTreeNode();
 
            SetSubTreeNode(node1, node2, node3);
            SetSubTreeNode(node2, node4, node5);
            SetSubTreeNode(node3, null, node6);
            SetSubTreeNode(node5, node7, null);
 
            int actual = TreeDepthHelper.GetTreeDepth(node1);
            Assert.AreEqual(actual, );
 
            ClearUpTreeNode(node1);
        }
 
        //               1
        //              /
        //             2
        //            /
        //           3
        //          /
        //         4
        //        /
        //
        [TestMethod]
        public void GetDepthTest2()
        {
            BinaryTreeNode node1 = new BinaryTreeNode();
            BinaryTreeNode node2 = new BinaryTreeNode();
            BinaryTreeNode node3 = new BinaryTreeNode();
            BinaryTreeNode node4 = new BinaryTreeNode();
            BinaryTreeNode node5 = new BinaryTreeNode();
 
            SetSubTreeNode(node1, node2, null);
            SetSubTreeNode(node2, node3, null);
            SetSubTreeNode(node3, node4, null);
            SetSubTreeNode(node4, node5, null);
 
            int actual = TreeDepthHelper.GetTreeDepth(node1);
            Assert.AreEqual(actual, );
 
            ClearUpTreeNode(node1);
        }
 
        // 1
        //  \
        //   2
        //    \
        //     3
        //      \
        //       4
        //        \
        //
        [TestMethod]
        public void GetDepthTest3()
        {
            BinaryTreeNode node1 = new BinaryTreeNode();
            BinaryTreeNode node2 = new BinaryTreeNode();
            BinaryTreeNode node3 = new BinaryTreeNode();
            BinaryTreeNode node4 = new BinaryTreeNode();
            BinaryTreeNode node5 = new BinaryTreeNode();
 
            SetSubTreeNode(node1, null, node2);
            SetSubTreeNode(node2, null, node3);
            SetSubTreeNode(node3, null, node4);
            SetSubTreeNode(node4, null, node5);
 
            int actual = TreeDepthHelper.GetTreeDepth(node1);
            Assert.AreEqual(actual, );
 
            ClearUpTreeNode(node1);
        }
 
        // 树中只有1个结点
        [TestMethod]
        public void GetDepthTest4()
        {
            BinaryTreeNode node1 = new BinaryTreeNode();
 
            int actual = TreeDepthHelper.GetTreeDepth(node1);
            Assert.AreEqual(actual, );
 
            ClearUpTreeNode(node1);
        }
 
        // 树中没有结点
        [TestMethod]
        public void GetDepthTest5()
        {
            int actual = TreeDepthHelper.GetTreeDepth(null);
            Assert.AreEqual(actual, );
        }
    }

　　（2）测试结果

　　①测试通过情况

　　②代码覆盖率

二、题目二：判断二叉树是否是平衡二叉树

2.1 题目说明

题目二：输入一棵二叉树的根结点，判断该树是不是平衡二叉树。如果某二叉树中任意结点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。例如，下图中的二叉树就是一棵平衡二叉树。

2.2 解题思路

　　（1）需要重复遍历节点多次的解法

　　有了求二叉树的深度的经验之后再解决这个问题，我们很容易就能想到一个思路：在遍历树的每个结点的时候，调用函数TreeDepth得到它的左右子树的深度。如果每个结点的左右子树的深度相差都不超过1，按照定义它就是一棵平衡的二叉树。

    public static bool IsBalancedBinaryTree(BinaryTreeNode root)
    {
        if (root == null)
        {
            return true;
        }
 
        int left = GetTreeDepth(root.LeftChild);
        int right = GetTreeDepth(root.RightChild);
        int diff = left - right;
 
        if (diff >  || diff < -)
        {
            return false;
        }
 
        return IsBalancedBinaryTree(root.LeftChild) && IsBalancedBinaryTree(root.RightChild);
    }

　　上面的代码固然简洁，但我们也要注意到由于一个结点会被重复遍历多次，这种思路的时间效率不高。例如在IsBalancedBinaryTree方法中输入上图中的二叉树，我们将首先判断根结点（结点1）是不是平衡的。此时我们往函数TreeDepth输入左子树的根结点（结点2）时，需要遍历结点4、5、7。接下来判断以结点2为根结点的子树是不是平衡树的时候，仍然会遍历结点4、5、7。毫无疑问，重复遍历同一个结点会影响性能。

　　（2）每个节点只需遍历一次的解法

　　换个角度来思考，如果我们用后序遍历的方式遍历二叉树的每一个结点，在遍历到一个结点之前我们就已经遍历了它的左右子树。只要在遍历每个结点的时候记录它的深度（某一结点的深度等于它到叶节点的路径的长度），我们就可以一边遍历一边判断每个结点是不是平衡的。

    public static bool IsBalancedBinaryTree(BinaryTreeNode root)
    {
        int depth = ;
        return IsBalancedBinaryTreeCore(root, ref depth);
    }
 
    private static bool IsBalancedBinaryTreeCore(BinaryTreeNode root, ref int depth)
    {
        if (root == null)
        {
            depth = ;
            return true;
        }
 
        int left = ;
        int right = ;
        if (IsBalancedBinaryTreeCore(root.LeftChild, ref left) && IsBalancedBinaryTreeCore(root.RightChild, ref right))
        {
            int diff = left - right;
            if (diff >= - && diff <= )
            {
                depth = left >= right ? left +  : right + ;
                return true;
            }
        }
 
        return false;
    }

　　在上面的代码中，我们用后序遍历的方式遍历整棵二叉树。在遍历某结点的左右子结点之后，我们可以根据它的左右子结点的深度判断它是不是平衡的，并得到当前结点的深度。当最后遍历到树的根结点的时候，也就判断了整棵二叉树是不是平衡二叉树。

2.3 单元测试

　　此方法的单元测试和第一种方法的一致，这里就不再贴出。需要注意的就是在针对二叉树的测试用例中，需要考虑两种：功能测试（平衡的二叉树，不是平衡的二叉树，二叉树中所有结点都没有左/右子树）。特殊输入测试（二叉树中只有一个结点，二叉树的头结点为NULL指针）。

作者：周旭龙

出处：http://edisonchou.cnblogs.com

本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文链接。