机器学习：偏差方差权衡（Bias Variance Trade off）

一、什么是偏差和方差

• 

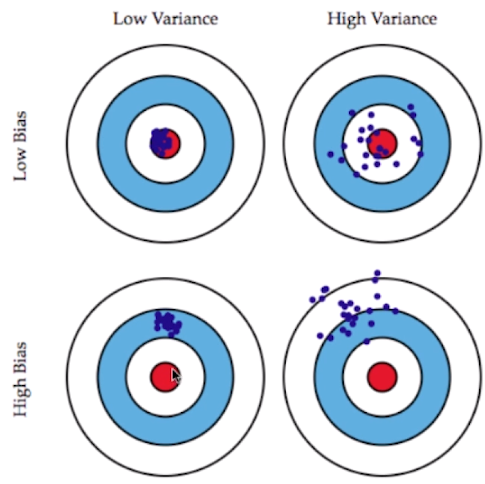
1. 偏差（Bias）：结果偏离目标位置；
2. 方差（Variance）：数据的分布状态，数据分布越集中方差越低，越分散方差越高；

• 在机器学习中，实际要训练模型用来解决一个问题，问题本身可以理解为靶心，而模型就是子弹，则子弹呈现在靶子上弹孔位置就可能出现偏差和方差的情况，也就是说训练出的模型可能犯偏差和方差两种错误；

二、 模型误差

• 模型误差 = 偏差（Bias） + 方差（Variance） + 不可避免的误差

　1）不可避免的误差

• 无能为力的、客观存在的、由于各种各样的原因导致的误差，是无论怎么改进算法和模型都无法避免的；如采集的数据本身含有的噪音。

• 偏差和方差是和算法及模型的相关问题。

　2）产生偏差和方差的原因

• 产生偏差的原因

1. 可能对问题本身的假设不正确；如非线性数据或问题使用线性回归算法。
2. 欠拟合（underfitting）会产生偏差；
3. 如果训练数据采用的特征跟问题的相关性不强或者根本没有相关性，就会使模型的预测结果偏离真实的结果。

• 方差产生的原因

1. 方差在机器学习中的表现为，数据的一点点扰动都会较大的影响模型，换句话说，模型没有完全学习到问题的实质，而学习到了很多噪音；
2. 模型太复杂，如高阶的多项式回归；
3. 过拟合（overfitting）会产生方差；

　3）高方差的算法

• 有一些算法天生就是高方差的算法；

1. 如 kNN，因为 kNN 有一个很大的缺点，对数据太敏感，因为模型每次都得找离被预测的样本最近的几个样本，让它们进行投票，但是这最近的几个样本一旦多数错误的结果，则导致预测的结果不准确。

• 一般非参数学习的算法都是高方差的算法

1. 因为这类算法不对数据进行任何假设，只能根据现有数据进行预测，因此它对训练数据的准确度依赖性比较高。换句话说，该类算法对训练数据比较敏感。（如 kNN、决策树）

　4）高偏差的算法

• 有一些算法天生是高偏差的算法；

1. 如线性回归，因为现实生活中很多问题可能不是线性关系，但如果非要使用线性手段拟合这些数据或问题，则会得到错误的结果，这类错误通常都是偏差错误。

• 一般参数学习的算法都是高偏差的算法，因为该类算法对数据具有极强的假设。

• 参数学习算法：将整个问题规约成一个数学模型，只需要求出该数学模型的参数即可。

1. 规约成数学模型的前提是对问题或数据进行假设，认为数据或问题的规律符合该数学模型，但是一旦数据或问题不符合该数学模型，也就是假设是错误的，会导致模型也是错误的，这种错误通常都是高偏差的错误。

三、解决模型误差

　1）机器学习算法中，大多数算法具有相应的参数，可以通过调参来调整模型的偏差和方差

•  kNN 算法

1. 对 k 的调整，其实就是在调整算法模型中引入的偏差和方差的错误，k 越小模型越复杂，相应的模型的方差越大偏差越小；k 越大模型越简单，直到 k 达到最大值（样本总数），此时 kNN 算法的本质就是看全部样本中哪类样本最多，就将此类样本的类型作为预测结果，这种情况下 kNN 算法的模型的方差最小偏差最大。

• 线性回归中使用多项式回归

1. 调整参数 degree，可改变线性回归算法模型的方差和偏差的误差。degree 越小模型越简单，模型的偏差越大方差越小；degree 越大模型越复杂，模型方差越大偏差越小。

　2）调整模型的偏差和方差

• 通常在一个机器学习算法中，偏差和方差是矛盾的，降低偏差就会提到方差，降低方差就会提高偏差，一般需要找到一个平衡；

• 如果一个算法模型的偏差和方差都较低，则算法本身可能存在错误，因为通常大部分情况下都不会这么理想。此时需要观察算法的主要错误是集中在偏差位置还是方差位置，并且要尝试使偏差和方差能不能达到平衡；换句话说，不要太高的方差，因为此情况下模型的泛化能力较弱；也不要太高的偏差，因为此情况下模型太过偏离原问题。

• 有时，可能不能完全杜绝错误，但让模型有一点偏差也有一点方差，而不是模型的错误集中在一个方面；通常在机器学习中，将模型调整到此种状态也是在对模型调参时要做的一个主要的事情。

• 机器学习领域的主要挑战，来自于方差：

1. 此说法只局限在算法的层面上，在问题的层面上不一定是这种情况。因为现实中人们还对很多问题的理解太过肤浅，比如对疾病和金融市场的理解。
2. 如，过去很多人尝试用历史的金融数据来预测未来的金融情况，通常预测的结果不够理想，很有可能历史的金融数据并不能很好的反应未来金融市场的走向，因此此种方法会带来很高的偏差。

• 现实中解决过拟合是很多算法工程师要解决的问题；

　3）解决高方差的通常手段

• 1）降低模型复杂度

1. 如多项式回归中，可通过较小 degree 来降低模型复杂度；

• 2）减少数据维度；降噪

1. 方差过大的大部分原因是模型学习的过多的噪音；

• 3）增加样本数

1. 也就是增大训练数据的规模：有时候算法具有高的方差，是因为模型太过复杂，模型中的参数非常多，而训练模型的样本数不足以支撑计算出这么多复杂的参数。（如：神经网络和深度学习）
2. 使用深度学习的一个非常重要的条件就是数据样本的规模必须足够的大，这样才能发挥深度学习算法的效用，其中的原因就是深度学习算法的模型太过复杂，模型中的参数非常多，而训练模型的样本数不足以支撑计算出这么多复杂的参数。否则的话，使用深度学习的算法在一个小样本上得到的结果，还不如使用简单的模型得到的结果。

　　　　

• 4）使用验证集

1. 在评测算法模型指标时需要使用 验证数据集（Validation），因为如果只使用 train_test_split 的方法得到的模型很有可能出现过拟合测试数据集的情况。

　　　　

• 5）模型的正则化