《计算机程式设计》Week3 课堂笔记

本笔记记录自 Coursera课程 《计算机程式设计》 台湾大学 刘邦锋老师

Week3 Array

3-1 Array Usage

例子：使用数组一次申明10个整数变量

int a[10]

这样就一次申明了10个整数的变量，a后面的方括号[10]表示a是一个有10个元素的整数数组。

所以说C语言中数组是用[ ]表示的。

【注】

• 一个数组和一个变量一样，有类别、名字、值、位址等属性，但数组还多了一个属性，就是数组中有几个元素。
• 因为数组中有多个元素，我们必须用一个数字代表我们要使用的是哪一个。这个数字就称为标注（index）。
• 与一般的数学向量惯例不同，C语言的数组标注是由0开始的。a[0]是数组a的第一个元素。

例子：(print-array.c)印出数组中元素的值

#include <stdio.h>

main()
{
    int a[10];
    int i;
    for (i = 0; i < 10; i++)
        scanf("%d", &(a[i]));
    for (i = 0; i < 10; i++)
        printf("%d\n", a[i]);
}

3-2 Inner Product

例子：(inner-product.c)计算内积

#include <stdio.h>
main()
{
    int A[5], B[5], C = 0;
    int i, j;
    for (i = 0; i < 5; i++)
        scanf("%d", &(A[i]));
    for (i = 0; i < 5; i++)
        scanf("%d", &(B[i]));
    for (i = 0; i < 5; i++)
        C += A[i] * B[i];
    printf("%d\n",C);
}

因为可以把数组看作是一个向量，两个向量之间就可以进行内积运算。

【注】这个程序的输入栏并不一定要一个数字一行，而是一个长度为5的向量一行，数字之间用一个空格隔开。这样会使输入更加清晰。因为scanf会在输入栏中持续找数字，一行没有找下一行，直到找到为止。所以对scanf完全没有影响。

3-3 Fibanacci Numbers

以费伯纳西数列为例，公式如下

\[fib(i)= \begin{cases} 0 & \text {i=0} \\ 1 & \text{i=1} \\ fib(i-1)+fib(i-2) & \text{i>=2} \end{cases}
\]

例子：(fib-array.c)计算费伯纳西数列到第n项

#include <stdio.h>
main()
{
    int i;
    int fab[100];
    int n;
    scanf("%d", &n);
    fab[0] = 0;
    fab[1] = 1;
    for (i = 2; i < n; i++)
        fab[i] = fab[i - 1] + fab[i - 2];
    for (i = 0; i < n; i++)
        printf("%d\n", fab[i]);
}

3-4 Prime Numbers

在数组中找到我们想要的数，比如说寻找第一个不为1的元素。

int array[10];
...
i = 0;
while (i < 10 && array[i] == 1)
    i++;

例子：(prime-array.c)印出n之内的质数

#include <stdio.h>
main()
{
    int composite[101];
    int i, n, j = 2;
    scanf("%d", &n);
    for (i = 2; i <= n; i++)
        composite[i] = 0;
    while (j * j <= n){
        while (composite[j] == 1)
            j++;
        for (i = 2 * j; i <= n; i += j)
            composite[i] = 1;
        j++;
    }
    for (i = 2; i <= n; i++)
        if (composite[i] == 0)
            printf("%d\n", i);
}

对于这个程序的思路是

• 利用一个数组composite作是否为合数的旗标(flag)。如果j是一个合数，那么对应的composite[j]为1，否则j是一个质数，composite[j]为0。
• 假设所有由2到n的整数都是质数。
• 由2开始，找第一个还没被设为合数的整数j，并认定为质数。
• 设定j的倍数为合数。
• 将j加1，测试下一个数。
• 只需测试到j * j <= n即可。

3-5 Bubble Sort

泡沫排序法

• 由左到右比较两个相邻元素，如果标注比较小的元素比较大，则交换元素值。
• 由标注比较小的元素两两交换到标注比较大的元素，就能使大的元素向标注比较大的方向移动，而小的元素向标注标比较小的方向移动。
• 用两层for循环实现。
  • 第一层循环决定两两交换的范围。
  • 第二层则实现两两交换。

例子：(bubble-sort.c)泡沫排序法

#include <stdio.h>
int main()
{
    int m, n[100];
    int i, j, temp;
    scanf("%d", &m);
    for (i = 0; i < m; i++)
        scanf("%d", &(n[i]));
    for (i = m -2; i >= 0; i--)
        for (j = 0; j <= i; j++)
            if (n[j] > n[j + 1]){
                temp = n[j];
                n[j] = n[j + 1];
                n[j + 1] = temp;
            }
    for (i = 0; i < m; i++)
        printf("%d\n", n[i]);
    return 0;
}

3-6 Array Address and Initialization

以十六进制打印出变量所在的记忆体位址

printf("%p\n", &i);

例子：(print-array-address.c)印出数组a中的元素的大小及位址

#include <stdio.h>
main()
{
    int a[10];
    int i;

    printf("%d\n", sizeof(a[0]));
    printf("%d\n", sizeof(a));
    for (i = 0; i < 10; i++)
        printf("%p\n", &(a[i]));
    printf("%p\n", &a);
    printf("%p\n", a);
}

对于上面这个程序

• a[0]是一个32位元的整数，所以会打印出4
• a是10个32位元的整数所组成的数组，所以会打印出40
• 数组a元素的记忆体位址是连续的，而且一个元素和下一个元素的位址刚好差4.
• 数组元素在记忆体中是由小排到大，而且每个元素占4个位元组。

所以元素a[i]的记忆体位址可用以下公式表示

\[a+(i \times L)
\]

其中，a为阵列a的起始位址，而L为每一元素所占的位元组数。a的位址和a[0]的位址是一样的（也就是一排房子的位置，从第一栋房子开始算）。

在C语言中，a的值并非代表数组中所有元素的值，而代表的是数组a的位址。

阵列的初始化

int array[5] = {1, 2, 3, 4, 5}；

跟变量的初始化差不多。而且[ ]中的5也可以不写，程序会自己计算{ }中有多少个元素。

如果数组申明有长度，也有初始化，但是初始化给的元素个数不够，那么其他的元素会默认初始化为0。

3-7 Multi-dimension Arrays

多维数组

比如说申明一个$ 3 \times 4 $的多维数组。

int a[3][4]；

例子：(matrix-multiply.c)矩阵相乘

#include <stdio.h>
main()
{
    int A[2][3], B[3][4], C[2][4];
    int i, j, k;

    for (i = 0; i < 2; i++)
        for (j = 0; j < 3; j++)
            scanf("%d", &(A[i][j]));
    for (i = 0; i < 3; i++)
        for (j = 0; j < 4; j++)
            scanf("%d", &(B[i][j]));
    for (i = 0; i < 2; i++)
        for (j = 0; j < 4; j++)
            C[i][j] = 0;
    for (i = 0; i < 2; i++)
        for (j = 0; j < 4; j++)
            for (k = 0; k < 3; k++)
                C[i][j] += A[i][k] * B[k][j];

    for (i = 0; i < 2; i++){
        for (j = 0; j < 4; j++)
            printf("%4d", C[i][j]);
        printf("\n");
    }
}

3-8 Multi-dimension Array Output with Newline

跟3-7差不多，主要将换行问题，可参考3-7最后C数组的输出方式。

3-9 Multi-dimension Array Address

例子：(print-matrix-address.c)三维数组大小及位址

#include <stdio.h>
main()
{
    int a[2][3][4];
    int i, j, k;

    printf("%d\n", sizeof(a[0][0][0]));
    printf("%d\n", sizeof(a[0][0]));
    printf("%d\n", sizeof(a[0]));
    printf("%d\n", sizeof(a));

    for (i = 0; i < 2; i++){
        for (j = 0; j < 3; j++){
            for (k = 0; k < 4; k++)
                printf("%p ", &(a[i][j][k]));
            printf("\n");
        }
        printf("\n");
    }

    for (i = 0; i < 2; i++)
        printf("%p ", &(a[i][1]));
    printf("\n");

    for (i = 0; i < 2; i++)
        printf("%p\n ", &(a[i][1]));
    printf("\n");

    for (i = 0; i < 2; i++)
        printf("%p\n", &(a[i]));
    printf("\n");

    for (i = 0; i < 2; i++)
        printf("%p\n", a[i]);
    printf("\n");

    printf("%p\n", &a);
    printf("%p\n", a);
}

【注】

• $ a[0][0][0] $是一个4个位元组的整数
• $ a[0][0] $是一个4个4个位元组的整数所组成的数组
• a包含两个矩阵，每个矩阵有三列，每一列都是一个有四个元素的一位数组

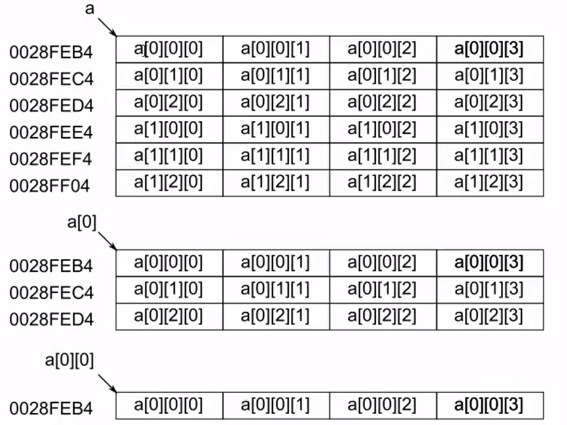
多维数组元素$ a[i][j][k] $ 的记忆体位址可以用以下的公式计算

\[a+(i \times 3 \times 4 + j \times 4 + k) \times 4
\]

具体一点则\(a[k_1][k_2]...[k_n]\)的记忆体位址是

\[a+(\sum_{i=1}^{n-1} (k_i \times \prod_{j=i+1}^n m_j) + k_n ) \times L
\]

3-10 Multi-dimension Array Address Example

3-9的程序运行结果讲解。

3-11 Multi-dimension Array Initialization

二维数列的初始化

int array[2][3] = {{1, 2, 3}, {4, 5, 6}};

跟一维数组很相似。可以写成\(array[][3]\)但不能写成\(array[][]\)。因为后者编译器无法决定位址。

补0原则仍然适用于多维数组。

3-12 Floating Point Input Output

float及double变量的申明方法

float f;
double df;

浮点数可以表示小数点。C语言里有两种浮点数，就是float和double。

float是一般浮点数，通常占4个位元组。

double是倍准(double precision)浮点数，通常占8个位元组，具有较高的准确度。

浮点数float的输出及输入

printf("%f\n", f);
scanf("%f", &f);

倍准浮点数double的输出及输入

printf("%f\n", df)；
scanf("%lf", &df)；

输出时，浮点数float及倍准浮点数double百分号%后面一律加f，因为printf会将float升级到倍准浮点数double再印出。

输入时浮点数在百分号%后面加f，倍准浮点数加lf。

3-13 Type Casting

混合类别计算

当一个算式同时出现不同类别的变量时，C语言采用一种升级的概念，就是等级低的会先被升级成等级高的，然后再计算。

倍准浮点数double的等级最高，再来是浮点数float，最后才是整数int。

除了因为算式中出现不同类别而发生的潜在类别转换之外，有时我们也需要直接将算式的类别做转换，此时我们就需要使用转型(cast)。

只要在算式前加一个用括号包住的类别，就可以将算式转换为该类别。

(type) expression

例子：(average.c)计算平均分数

#include <stdio.h>
int main()
{
    int count = 0;
    int sum = 0;
    int grade;
    double average;

    scanf("%d", &grade);
    while (grade >= 0){
        sum += grade;
        count++;
        scanf("%d", &grade);
    }
    average = sum / count;
    printf("%f\n", average);
    average = (double) sum / count;
    printf("%f\n", average);
    average = (double) (sum / count);
    printf("%f\n", average);
}

3-14 Floating Point Computation

以计算\(e^x\) 的泰勒展开式为例。

\[e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+...+\frac{x^n}{n!}
\]

思路是使用一个for循环来计算每一次的\(\frac{x^i}{i!}\)值。分子的部分存在x_power，分母的阶乘部分存在factorial。

例子：(e-x-float.c)以float计算\(e^x\)

#include <stdio.h>
mian()
{
    float x;
    float e = 1.0;
    int i;
    int n = 10;
    int factorial = 1;
    float xpower = 1.0;

    scanf("%f", &x);
    for (i = 1; i <= n; i++){
        factorial *= i;
        xpower *= x;
        e += xpower / factorial;
    }
    printf("%f\n", e);
}

上面的程序中变量factorial是来计算分母的阶乘的。而阶乘增加的非常快，当输入的n稍大时，变量factorial 就会发生溢位，影响计算结果。

改善的方法是不要直接计算分子分母，而是使用一个变量term记住目前的第i项\(\frac{x^i}{i!}\)，然后调整成第i+1项\(\frac{x^{i+1}}{(i+1)!}\)即可。

#include <stdio.h>
mian()
{
    double x;
    double e = 1.0;
    int i;
    int n = 20;
    double term = 1.0;

    scanf("%lf", &x);
    for (i = 1; i <= n; i++){
        term *= (x/i);
        e += term;
    }
    printf("%f\n", e);
}

测验代码

啊……这次测验要写的代码好难啊…………

贴出老师的代码

#include <stdio.h>

int main ()
{
   int n, m;
   int num;
   int w_flag = 0;
   scanf ( "%d%d", &n, &m );

   int board[n][m][m];
   int bingo[n][2][m+1];

   for ( int p = 0; p < n; p++ ) {
      for ( int i = 0; i < m; i++ ) {
         bingo[p][0][i] = bingo[p][1][i] = 0;
         for ( int j = 0; j < m; j++ )
            scanf ( "%d", &board[p][i][j] );
      }
      bingo[p][0][m] = bingo[p][1][m] = 0;
   }

   while ( !w_flag ) {
      // read number
      scanf ( "%d", &num );

      // for each player find number in their board
      for ( int p = 0; p < n; p++ ) {
         int f_flag = 0;
         for ( int i = 0; !f_flag && i < m; i++ )
            for ( int j = 0; !f_flag && j < m; j++ )
               // mark if find
               if ( board[p][i][j] == num ) {
                  f_flag = 1;
                  // row and column
                  bingo[p][0][i]++;
                  bingo[p][1][j]++;
                  // diagnal
                  if ( i == j ) bingo[p][0][m]++;
                  if ( i + j == m-1 ) bingo[p][1][m]++;
                  // win
                  if ( bingo[p][0][i] == m || bingo[p][1][j] == m ||
                       bingo[p][0][m] == m || bingo[p][1][m] == m ) {
                     if ( !w_flag ) {
                        printf ( "%d", num );
                        w_flag = 1;
                     }
                     printf ( " %d", p );
                  }
               }
      }

   }

   return 0;
}

老师是建议大家可以在ideone上进行代码的编译的，但是这个在线的网站是要魔法上网的，不过毕竟大家都coursera上看到了视频应该都会魔法上网了。

但是有一个小建议，可以现在notepad++这类软件上先把代码写好再复制粘贴到网页上编译，而不是直接在网页上写。因为……很容易手贱一刷新网页就崩了！写了的代码全没了的情况，别问我是怎么知道的。