bzoj2564: 集合的面积（闵可夫斯基和 凸包）

题面

传送门

题解

花了一个下午的时间调出了一个稍微能看的板子……没办法网上的板子和咱的不太兼容……

首先有一个叫做闵可夫斯基和的东西，就是给你两个点集\(A,B\)，要你求一个点集\(C=\{x+y\mid x\in A,y\in B\}\)，\(C\)就是\(A,B\)的闵可夫斯基和

我们考虑一下如果\(B\)只有一个点，那么\(C\)就可以看做\(A\)向某个方向平移一段距离，所以\(C\)就可以看做\(A\)向\(|B|\)个方向平移的点集的并集

然后我们现在想要求出\(C\)的凸包

首先原来不在\(A\)的凸包上的点平移之后也肯定不在凸包上，所以我们可以先求出\(A\)的凸包

我们先来考虑合并两个凸壳的情况。借（dao）用（yong）一下\(shadowice\)巨巨的图

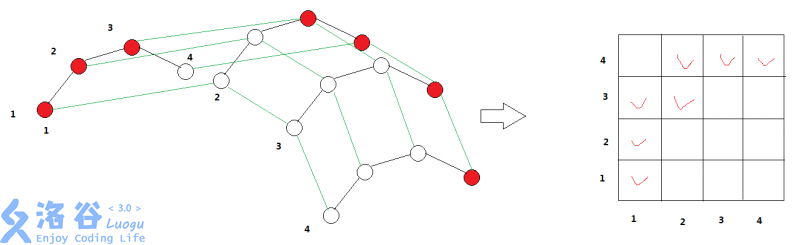
对于图中每个点，如果它是\(i\)和\(j\)加起来得到的话，我们就把它标号为\((i,j)\)，然后把这张图变成一个表格。然后我们发现，凸包中的点构成一个从\((1,1)\)到\((|A|,|B|)\)的路径，而且只能往上或往右走

那么我们就可以用双指针来维护了，设当前在\((i,j)\)，每次看一下\((i+1,j)\)和\((i,j+1)\)两个点哪个在新的凸包上，然后走过去

为了避免我们求出的凸包是个有三点共线的假凸包，再对\(C\)跑一个凸包就好了（虽然这里求的是面积所以不跑也可以然而咱的板子不知为何不重新求就会\(WA\)而且重新求跑得比不重新求还要快……）

//minamoto
#include<bits/stdc++.h>
#define R register
#define inf 0x3f3f3f3f
#define ll long long
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
using namespace std;
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
int read(){
    R int res,f=1;R char ch;
    while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
    for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
    return res*f;
}
const int N=2e5+5;
struct node{
	int x,y;
	node(){}
	node(R int xx,R int yy):x(xx),y(yy){}
	inline node operator +(const node &b)const{return node(x+b.x,y+b.y);}
	inline node operator -(const node &b)const{return node(x-b.x,y-b.y);}
	inline ll operator *(const node &b)const{return 1ll*x*b.y-1ll*y*b.x;}
	inline ll norm(){return 1ll*x*x+1ll*y*y;}
}A[N],B[N],C[N],st[N],P;
int ta,tb,tc,n,m,k,top;ll res;
inline bool cmp(const node &a,const node &b){
	ll k=(a-P)*(b-P);
	return k?(k>0?1:0):(a-P).norm()<(b-P).norm();
}
void Graham(node *A,int &ta){
	P=node(inf,inf),k=0;
	fp(i,1,ta)if(A[i].x<P.x||A[i].x==P.x&&A[i].y<P.y)P=A[i],k=i;
	swap(A[1],A[k]),sort(A+2,A+1+ta,cmp);
	st[0]=A[1],st[top=1]=A[2];
	fp(i,3,ta){
		while(top&&(A[i]-st[top-1])*(st[top]-st[top-1])>=0)--top;
		st[++top]=A[i];
	}
	fp(i,0,top)A[i]=A[i+top+1]=st[i];
	ta=top;
}
void merge(){
	C[tc=1]=A[0]+B[0];
	R int i=0,j=0;
	while(i<=ta&&j<=tb){
		node p1=(A[i]+B[j+1])-C[tc],p2=(A[i+1]+B[j])-C[tc];
		p1*p2>=0?(C[++tc]=A[i]+B[j+1],++j):(C[++tc]=A[i+1]+B[j],++i);
	}
	for(;i<=ta;++i)C[++tc]=A[i]+B[j];
	for(;j<=tb;++j)C[++tc]=A[i]+B[j];
	Graham(C,tc);
	fp(i,0,tc)res+=C[i]*C[i+1];
	printf("%lld\n",res);
}
int main(){
//	freopen("testdata.in","r",stdin);
	n=read(),m=read(),ta=n,tb=m;
	fp(i,1,n)A[i].x=read(),A[i].y=read();
	fp(i,1,m)B[i].x=read(),B[i].y=read();
	Graham(A,ta),Graham(B,tb);
	merge();
	return 0;
}