【luogu P3390 矩阵快速幂】 模板

题目链接：https://www.luogu.org/problemnew/show/P3390

首先要明白矩阵乘法是什么

对于矩阵A m*p  与  B p*n 的矩阵 得到C m*n 的矩阵

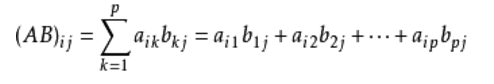
矩阵乘法满足结合律，但不满足交换律（所以可以套快速幂的板子）

进行矩阵乘法时要么重载*号，或者是写一个矩阵相乘的函数

 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 using namespace std;
 struct Matrix{
     long long m[][];
 }A,E;
 long long n,k,mod = ;
 Matrix mul(Matrix A,Matrix B)
 {
     Matrix C;
     for(long long i = ; i < n; i++)
         for(long long j = ; j < n; j++)
         {
             C.m[i][j] = ;
             for(long long k = ; k < n; k++)
                 C.m[i][j] = (C.m[i][j]+(A.m[i][k]*B.m[k][j])%mod)%mod;
         }
     return C;
 }
 Matrix fast(Matrix A, long long k)
 {
     Matrix S = E;
     while(k)
     {
         if(k&) S = mul(S,A);
         A = mul(A,A);
         k = k>>;
     }
     return S;
 }
 int main(){

     scanf("%lld%lld",&n,&k);
     for(long long i = ; i < n; i++)
         for(long long j = ; j < n; j++)
         scanf("%lld",&A.m[i][j]);

     for(long long i = ; i < n; i++) E.m[i][i] = ;
     Matrix ans = fast(A,k);
     for(long long i = ; i < n; i++)
     {
         for(long long j = ; j < n-; j++)
         printf("%lld ",(ans.m[i][j])%mod);
         printf("%lld\n",(ans.m[i][n-])%mod);
     }
     return ;
 }